南阳市2019年秋期高中三年级期终质量评估数学试题（理） 14页

南阳市2019年秋期高中三年级期终质量评估数学试题（理）‎ 注意事项：‎ ‎1.本试卷分第1卷（选择题）和第11卷（非选择题）两部分，考生做题时将答案答在答题卡的指定位置上，在本试卷上答题无效.‎ ‎2.答题前，考生务必先将自己的姓名、准考证号填写在答题卡上.‎ ‎3.选择题答案使用2B铅笔填涂，非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整，笔迹清楚.‎ ‎4.请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效.‎ ‎5.保持卷面清洁，不折叠、不破损.‎ 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ 1. 已知集合，，则 A. B. C. D. 答案：A 2. 设复数（为虚数单位），则复数的虚部为 A. B. C. D. 答案：C 3. 在一个不透明的容器中有6个小球，其中有4个黄球，2个红球，它们除颜色外完全相同，如果一次随机取出2个球，那么至少有1个红球的概率为 A.‎ ‎ B. C. D. 答案：B 1. 已知函数（的最小正周期为，则下列说法正确的是 A.函数的图像关于对称 B.函数的图像关于对称 C.函数的图像关于直线对称 D.函数的图像关于直线对称 答案：B 2. 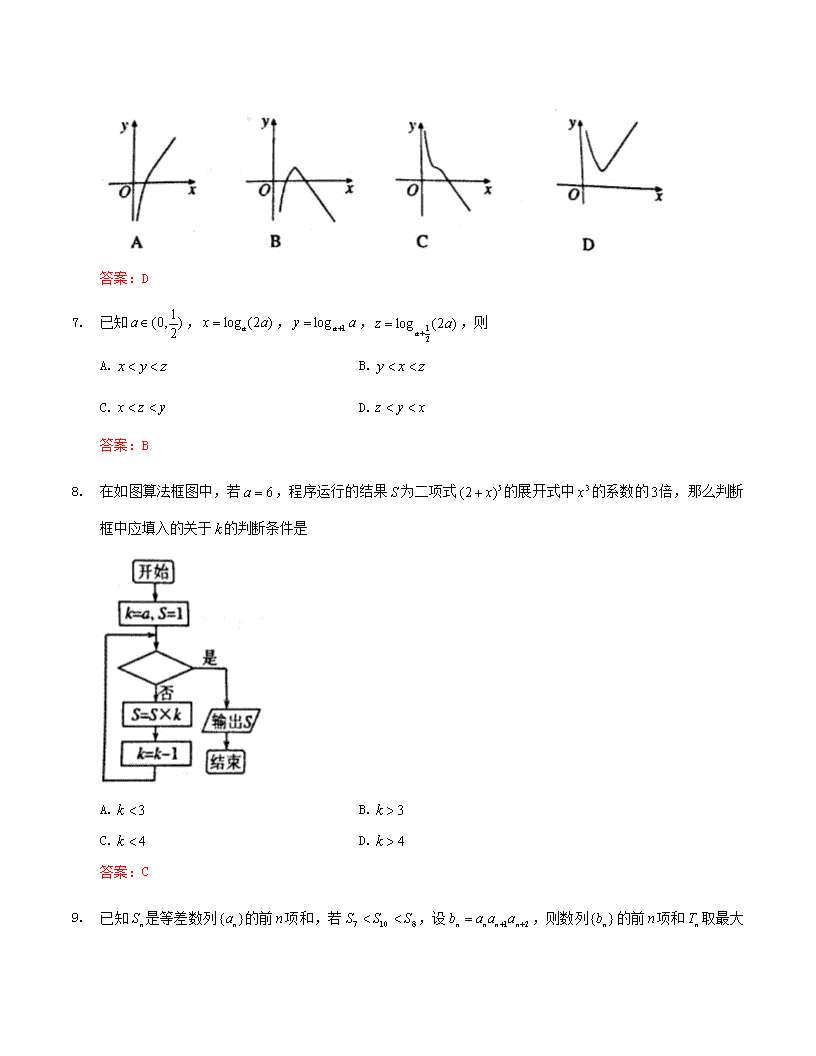甲、乙两类水果的质量（单位：）分别服从正态分布，，其正态分布的密度曲线如图所示，则下列说法错误的是 A.甲类水果的平均质量 B.甲类水果的质量比乙类水果的质量更集中于平均值左右 C.甲类水果的平均质量比乙类水果的平均质量小 D.乙类水果的质量服从的正态分布的参数 答案：D 3. 函数的大致图像为 ‎ 答案：D 1. 已知，，，，则 A. B. C. D. 答案：B 2. 在如图算法框图中，若，程序运行的结果为二项式的展开式中的系数的倍，那么判断框中应填入的关于的判断条件是 A. B. C. D. 答案：C 3. 已知是等差数列的前项和，若，设，则数列的前项和取最大值时 的值为 A. B. C. D. 答案：D 1. 十八世纪，函数（表示不超过的最大整数）被“数学王子”高斯采用，因此得名为高斯函数，结合定义的表述，人们习惯称为“取整函数”，根据上述定义，则方程的所有实数根的个数为 A. B. C. D. 答案：C 2. 某三棱锥的三视图如图所示，其中主视图是等边三角形，则该三棱锥外接球的表面积为 A. B. C. D. 答案：D 3. 已知函数，若函数的零点均在区间（，，）内，则的最小值是 A. B. C. ‎ D. 答案：A 二、填空题（本大题共4小题，每小题5分，共20分）‎ 1. 已知向量，，若，则实数的值为________. 答案：‎ 2. 学校准备将名同学全部分配到运动会的田径、拔河和球类个不同项目比赛做志愿者，每个项目至少名，则不同的分配方案有________种（用数字作答）. 答案：150‎ 3. 已知双曲线的左右两个焦点分别为，，，为其左、右两个顶点，以线段为直径的圆与双曲线的渐近线在第一象限的交点为，且，则该双曲线的离心率为________. 答案：‎ 4. 已知函数（为自然对数的底数，，为常数）有三个不同的零点，则实数的取值范围为________. 答案：‎ 三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答，第22，23题为选考题，考生根据要求作答.）‎ 5. ‎（本小题满分12分） 如图，在中，角，，的对边分别为，，，且. （1）求的大小； （2）若，点、在的异侧，，，求平面四边形面积的最大值. ‎ 解析：（1）因为，且， 所以……………………………………………………1分 在中， 所以…………………………………………2分 所以 所以……………………………………………………3分 因为在中， 所以 ……………………………………………………………4分 因为是的内角 所以∠ACB=.…………………………………………………………………5分 （2）在中，…………………………6分 因为是等腰直角三角形， 所以 ……………………………………………7分 ………………………………………………………8分 所以平面四边形的面积 ………………………9分 因为 ‎，所以……………………………………………10分 所以当即时，， …………………………11分 此时平面四边形的面积有最大值.…………………………12分 1. ‎（本小题满分12分） 如图，在四棱锥中，底面为菱形，底面，，，是上的一点，. （1）证明：平面； （2）若二面角为直二面角，求与平面所成角的大小. 解析：设以O为原点，OC，OD分别为轴、轴建立空间直角坐标系则设 .............2分 证明：由PE=2EC得 所以，，所以PC⊥BE，PC⊥BD，又， 所以PC⊥平面BDE. .............5分 （2）设平面PAB的法向量为=,又， 由取 ‎= .............7分 设平面PBC的法向量为=,又， 由取= .............9分 由题意得， .........10分 ， 又 .............11分 所以PD与平面PBC所成角的正弦值为，PD与平面PBC所成角为 .............12分 1. ‎（本小题满分12分） 设直线与抛物线交于，两点，与椭圆交于，两点，设直线，，，（为坐标原点）的斜率分别为，，，，若. （1）证明：直线过定点，并求出该定点的坐标； （2）是否存在常数，满足？并说明理由. 解析：（1）证明：由题知，直线的斜率存在且不过原点， 故设， 由可得，. ............2分 OA⊥OB.,，故 ............4分 所以直线的方程为 故直线恒过定点（0,2）. ............5分 （2‎ ‎）由（1）知 ............7分 设 由可得， .............9分 ......11分 ，即存在常数满足题意. ............12分 1. ‎（本小题满分12分） 已知函数 （1）若函数有个零点，求实数的取值范围； （2）若关于的方程有两个不等实根，，证明：①；②. 解析：（1）由题知，与有两个交点，， .... 1分 由得，；由得，， 在上单增，在上单减， ...........3分 又,且时，，故 ...........4分 （2）①方程可化为，令，， 所以在 上单增，在上单减，又 ...........6分 不妨设.则，要证明只需证 且在上单减，所以证 令， ............7分 则 当时，， 即在单增.又， ..........8分 对恒成立，即成立 即成立 ............10分 ②由①得,即，命题得证. ...12分 ‎ 1. ‎（本小题满分12分） 一种掷硬币走跳棋的游戏：在棋盘上标有第1站、第2站、第3站、…、第100站，共100站，设棋子跳到第站的概率为，一枚棋子开始在第1站，棋手每掷一次硬币，棋子向前跳动一次.若硬币的正面向上，棋子向前跳一站；若硬币的反面向上，棋子向前跳两站，直到棋子跳到第站（失败）或者第站（获胜）时，游戏结束. （1）求，，； （2）求证：数列（=1，2，3，…，98）为等比数列； ‎ ‎（3）求玩该游戏获胜的概率. 解析：（1）棋子开始在第1站是必然事件，； 棋子跳到第2站，只有一种情况，第一次掷硬币正面向上，其概率为; 棋子跳到第3站，有两种情况，①第一次掷硬币反面向上，其概率为；②前两次掷硬币都是正面向上，其概率为，; .......................3分 （2）棋子棋子跳到第n+2（）站，有两种情况：①棋子先跳到第站，又掷硬币反面向上，其概率为；②棋子先跳到第站，又掷硬币正面向上，其概率为.故 ......................5分 又， 数列是以为首项，为公比的等比数列. ................7分 (3)由（2）得. ...............8分 ...............11分 所以获胜的概率为 ...............12分 （说明：‎ ‎①若计算出当做获胜的概率扣2分； ②获胜的概率也可以由求得）‎ ‎（二）选考题：共10分、请考生在第22，23题中任选一题作答，如果多做，那么按所做的第一题计分.‎ 1. ‎（本小题满分10分） 在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，且曲线与恰有一个公共点. （1）求曲线的极坐标方程； （2）已知曲线上两点，满足，求面积的最大值. 解析：(Ⅰ)曲线极坐标方程可化为， 将代入上式可得直角坐标方程为， 即，所以曲线为直线． ......................2分 又曲线是圆心为,半径为的圆， 因为圆与直线恰有一个公共点， 所以， 所以圆的普通方程为， ....................4分 把代入上式可得的极坐标方程为， 即. ......................5分 (Ⅱ)‎ 由题意可设， ， ......................8分 所以当时，的面积最大，且最大值为. .......................10分 1. ‎（本小题满分10分） 若关于的不等式有解，记实数的最大值为. （1）求的值； （2）若正数，，满足，求的最小值. 解析：（1）设 所以的值域为, .......................3分 故，解得 .........................5分 （2）由（1）知即 .........................9分 ‎ ‎（当且仅当即时取等号） 故的最小值为. ...............................10分