2021届高考数学一轮复习专题六立体几何第1课时课件 27页

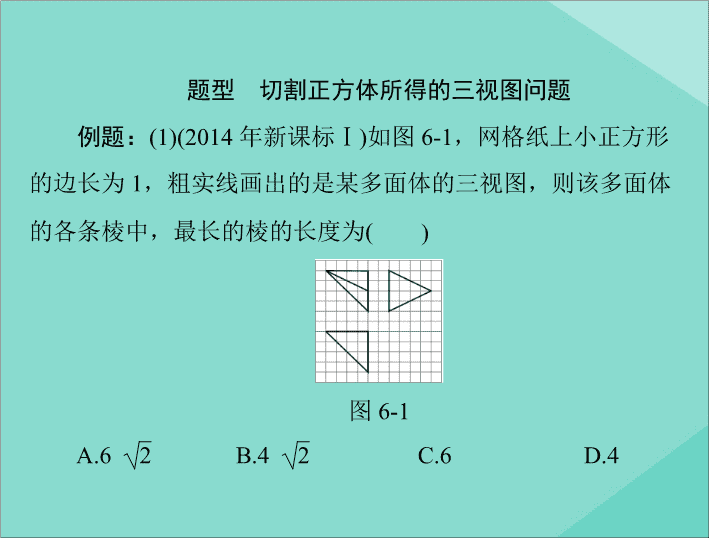
专题六 立体几何 第 1 课时 题型 切割正方体所得的三视图问题 例题： (1)(2014 年新课标 Ⅰ ) 如图 6-1 ，网格纸上小正方形 的边长为 1 ，粗实线画出的是某多面体的三视图， 则该多面体 ) 的各条棱中，最长的棱的长度为 ( 图 6-1 解析： 根据题意，得该几何体是如图 6-2 所示的三棱锥 A - BCD ，且该三棱锥是放在棱长为 4 的正方体中，∴在三棱锥 ＝ 6. 图 6-2 答案： C (2)(2017 年北京 ) 某三棱锥的三视图如图 6-3 ，则该三棱锥 的体积为 ( ) 图 6-3 A.60 B.30 C.20 D.10 解析： 如图 6-4 ，把三棱锥 A - BCD 放到长方体中，长方体 的长、宽、高分别为 5,3,4 ， 图 6-4 △ BCD 为直角三角形，直角边分别为 5 和 3 ，三棱锥 A - BCD 的高为 4 ， 答案： D (3)(2016 年北京 ) 某三棱锥的三视图如图 6-5 ，则该三棱锥 的体积为 ( ) 图 6-5 A. 1 6 B. 1 3 C. 1 2 D.1 解析： 由三视图可得该几何体的直观图为三棱锥 A - BCD ， 将其放在长方体中如图 6-6 ，其中 BD ＝ CD ＝ 1 ， CD ⊥ BD ， 三棱锥的高为 1 ， 图 6-6 答案： A (4)(2018 年北京 ) 某四棱锥的三视图如图 6-7 ，在此四棱锥 ) 的侧面中，直角三角形的个数为 ( 图 6-7 A.1 个 B.2 个 C.3 个 D.4 个 解析： 如图 6-8 ，该四棱锥的侧面中，直角三角形有△ ABE ， △ ABC ，△ ADE ，共 3 个 . 图 6-8 答案： C (5) 已知一个棱长为 2 的正方体被两个平面所截 得的几何体 ) 的三视图 ( 单位： cm) 如图 6-9 ，则该几何体的体积是 ( 图 6-9 解析： 由三视图得原几何体如图 6-10 所示，在正方 体 ABCD - A 1 B 1 C 1 D 1 中，由平面 AB 1 D 1 ，平面 CB 1 D 1 截得的几何体 的体积为一个正方体的体积减去两个底面为等腰直角三角形的 图 6-10 答案： D (6) 如图 6-11 ，网格纸上正方形小格的边长为 1 ，粗线画出 ) 的是某几何体的三视图，则该几何体的最长棱的长度为 ( 图 6-11 图 6-12 答案： C (7) 如图 6-13 ，虚线小方格是边长为 1 的正方形，粗实 ( 虚 ) ) 线为某几何体的三视图，则该几何体外接球的表面积为 ( 图 6-13 A.4π B.8π C.16π D.32π 解析： 几何体的直观图如图 6-14 所示的三棱锥 O - ABC ， 图 6-14 三棱锥 O - ABC 中，∠ AOC ＝∠ ABC ＝ 90° ， ∴ 外接球的直径为 AC . ∴ 外接球的表面积 S ＝ 4π R 2 ＝ 32π. 答案： D ) (8) 一个四棱锥的三视图如图 6-15 ，则其体积为 ( 图 6-15 A.11 B.12 C.13 D.16 16. 图 6-16 答案： D (9) 如图 6-17 ，网格纸上正方形小格的边长为 1 ，图中粗线 ) 画的是某几何体的三视图，则该几何体最长棱的长度为 ( 图 6-17 解析： 几何体如图 6-18 ，则该几何体最长棱 的长度为正方 图 6-18 答案： D (10) 已知一个三棱锥的三视图如图 6-19 ，正视图和俯视图 都是直角梯形， 侧视图是正方形，则该几何体最长的棱长为 ( ) 图 6-19 解析： 几何体如图 6-20 ，则该几何体最长的棱长为 CD ＝ 图 6-20 答案： D (11) 如图 6-21 ，网格纸上小正方形的边长为 1 ，粗线画出的 ) 是某三棱锥的三视图，则该几何体的体积为 ( 图 6-21 A.4 B.2 C. 4 3 D. 2 3 图 6-22 答案： D (12) 如图 6-23 ，网格纸上小正方形的边长为 1 ，粗线画出的 ) 是某个四面体的三视图，则该四面体的表面积为 ( 图 6-23 解析： 该几何体为图 6-24 中的三棱锥 C - A 1 C 1 E ， 图 6-24 答案： A (13)(2018 年上海模拟 ) 如图 6- 25 是某几何体的三视图，则 此几何体的体积是 ( ) 图 6-25 A. 11 3 B. 8 3 C. 16 3 D. 22 3 解析： 根据三视图知此几何体是边长为 2 的正方体截去一 个三棱锥 P - ABC 剩下的部分 ( 如图 6-26) ，∴此几何体的体积为 图 6-26 答案： D