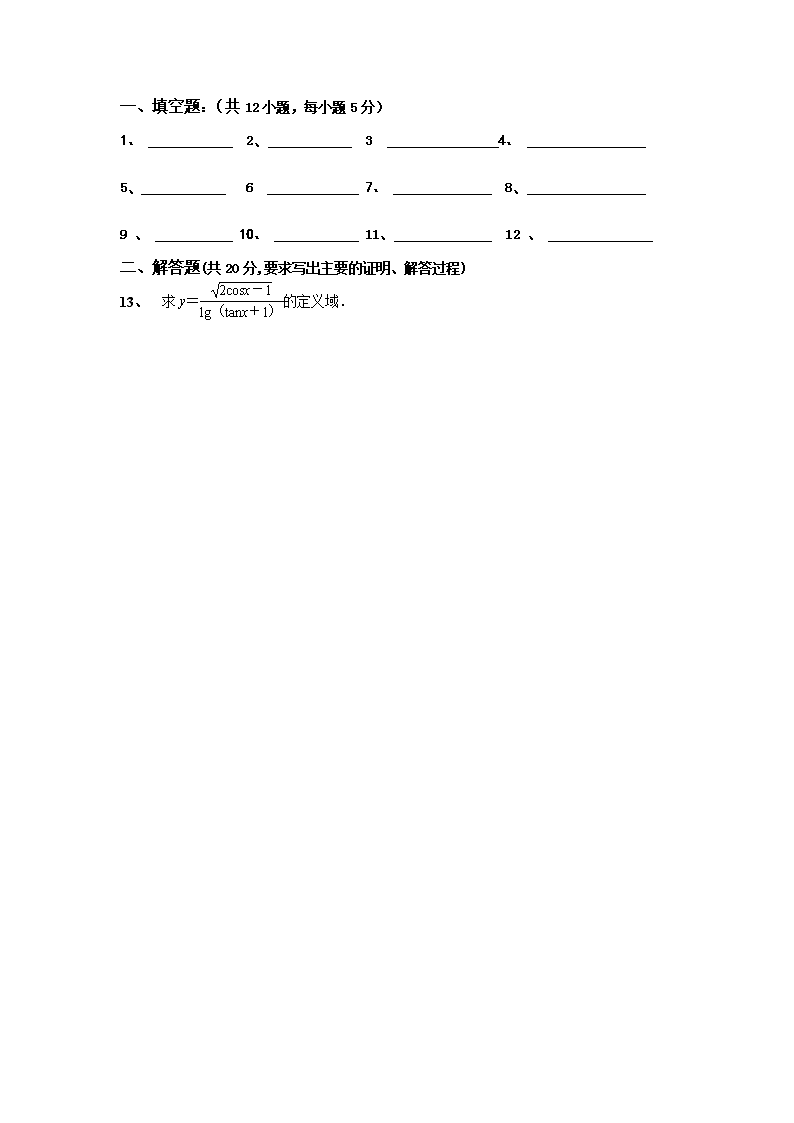【数学】2020届一轮复习苏教版三角函数的性质（1）课时作业 3页

数学高考小题专题复习练习 三角函数的性质（1） 一、填空题（共 12 题，每题 5 分） １、函数 的定义域为 ． 2、函数 的最小正周期是 ． 3、求函数 的定义域为 ． 4、函数 的最小正周期为 ． 5、函数 的定义域为 ． 6、已知函数 ，则下面结论错误的序号是　　 ①函数 的最小正周期为 2 ②函数 在区间［0， ］上是增函数 ③函数 的图象关于直线 ＝0 对称 ④函数 是奇函数　 7、已知函数 ，且 ，则 的值是 ． 8、当 ，不等式 成立，则实数 的取值范围是_______________. 9、已知 f(x)＝sin(x＋θ)＋ 3cos(x－θ)为偶函数，则 tanθ= ． 10、定义在 R 上的函数 既是偶函数又是周期函数.若 的最小正周期是 ，且当 时， ，则 的值为 ． 11、已知函数 .项数为 27 的等差数列 满足 ，且公 差 .若 ，则当 =____________时，有 ． 12、已知函数 f(x)=sin 2 ωx+ sinωxsin( ωx+ )(ω＞0)的最小正周期为π.则ω的值 =____________． 数学高考小题专题复习练习答题纸 班级 姓名 分数 )4tan( π−= xy 1)4(cos2 2 −−= π xy 1sin cos2y x x= − + ( ) (1 3 tan )cosf x x x= + xxy tanlog9 3 2 +−= ))(2sin()( Rxxxf ∈−= π )(xf π )(xf 2 π )(xf x )(xf ( ) sin 1f x ax b x= + + ( )5 7f = ( )5f − 时10 ≤≤ x kxx ≥ 2sin π k )(xf )(xf π ]2,0[ π∈x xxf sin)( = )3 5( π f xxxf tansin)( += { }na     −∈ 22 ππ ，na 0≠d 0)()()( 2721 =+…++ afafaf k 0)( =kaf 3 2 π 一、填空题：（共 12 小题，每小题 5 分） 1、 2、 3 4、 5、 6 7、 8、 9 、 10、 11、 12 、 二、解答题(共 20 分,要求写出主要的证明、解答过程) 13、 求 y＝ 2cosx－1 lg（tanx＋1）的定义域． 三角函数的性质（1） １． ；2． ；3． 4． ；5． ；6．④；7．-5 提示：利用 ８．k≤1　　作出 与 的图象，要使不等式 成立，由图可知须 k≤ 1．9．－ 3 提示：sin(－x＋θ)＋ 3cos(―x―θ)＝sin(x＋θ)＋ 3cos(x－θ) 3[cos(x＋θ)―cos(x― θ)]＝sin(x＋θ)＋sin(x―θ) ―2 3sinθsinX＝2sinXcosθ． ∵sinX 不恒为 0．∴tanθ＝－3． 10． 提示： 11. 14　　函数 在 是增函数，显然又为奇函数，函数图象关于原点对称， 因为 ， 所以 ，所以当 时， . 12. 1 提示： 因为函数 f(x)的最小正周期为π,且ω＞0,所以 解得ω=1. 13. 解：由题意得 (k Z) 2kπ－π 4＜x＜2kπ 或 2k + ≥− 11tan 01tan 01cos2 x x x ⇒        ≠ −> ≥ 0tan 1tan 2 1cos x x x ⇒         ≠ +<<− +≤≤− π ππππ ππππ kx kxk kxk 4 3242 3232 ∈ ⇒ π π