2020届二轮复习立体几何的动态问题学案（全国通用） 8页

专题03 立体几何的动态问题 一．方法综述 立体几何的动态问题是高考的热点，问题中的“不确定性”与“动感性”元素往往成为生思考与求解问题的思维障碍，使考题的破解更具策略性、挑战性与创新性。一般立体动态问题形成的原因有动点变化、平面图形的翻折、几何体的平移和旋转以及投影与截面问题，由此引发的常见题型为动点轨迹、角度与距离的计算、面积与体积的计算、探索性问题以及有关几何量的最值求解等。此类题的求解并没有一定的模式与固定的套路可以沿用，很多生一筹莫展，无法形成清晰的分析思路，导致该题成为生的易失分点。究其原因，是因为生缺乏相关素养和解决问题的策略造成的。‎ 动态立体几何题在变化过程中总蕴含着某些不变的因素，因此要认真分析其变化特点，寻找不变的静态因素，从静态因素中，找到解决问题的突破口。求解动态范围的选择、填空题，有时应把这类动态的变化过程充分地展现出来，通过动态思维，观察它的变化规律，找到两个极端位置，即用特殊法求解范围。对于探究存在问题或动态范围（最值）问题，用定性分析比较难或繁时，可以引进参数，把动态问题划归为静态问题。具体地，可通过构建方程、函数或不等式等进行定量计算，以算促证。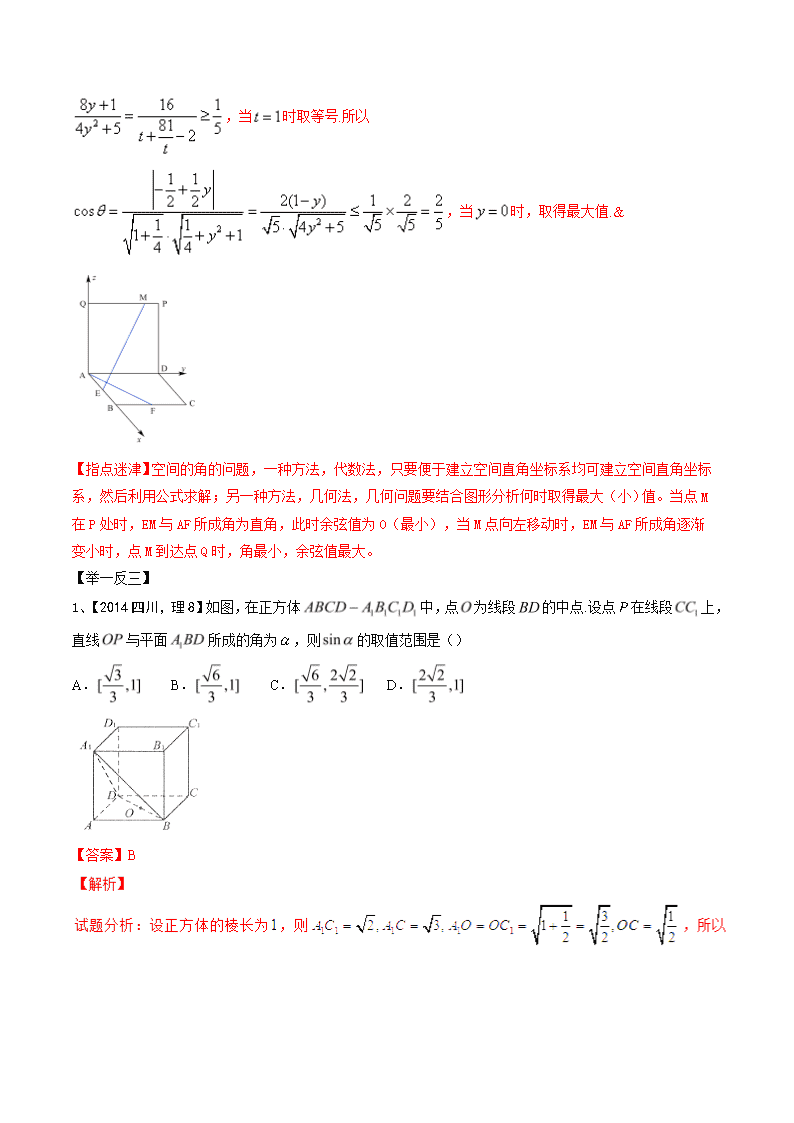‎ 二．解题策略 类型一 立体几何中动态问题中的角度问题 例1.【2015高考四川，理14】如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为，则的最大值为.‎ ‎【答案】‎ ‎，当时取等号.所以，当时，取得最大值.&‎ ‎【指点迷津】空间的角的问题，一种方法，代数法，只要便于建立空间直角坐标系均可建立空间直角坐标系，然后利用公式求解；另一种方法，几何法，几何问题要结合图形分析何时取得最大（小）值。当点M在P处时，EM与AF所成角为直角，此时余弦值为0（最小），当M点向左移动时，EM与AF所成角逐渐变小时，点M到达点Q时，角最小，余弦值最大。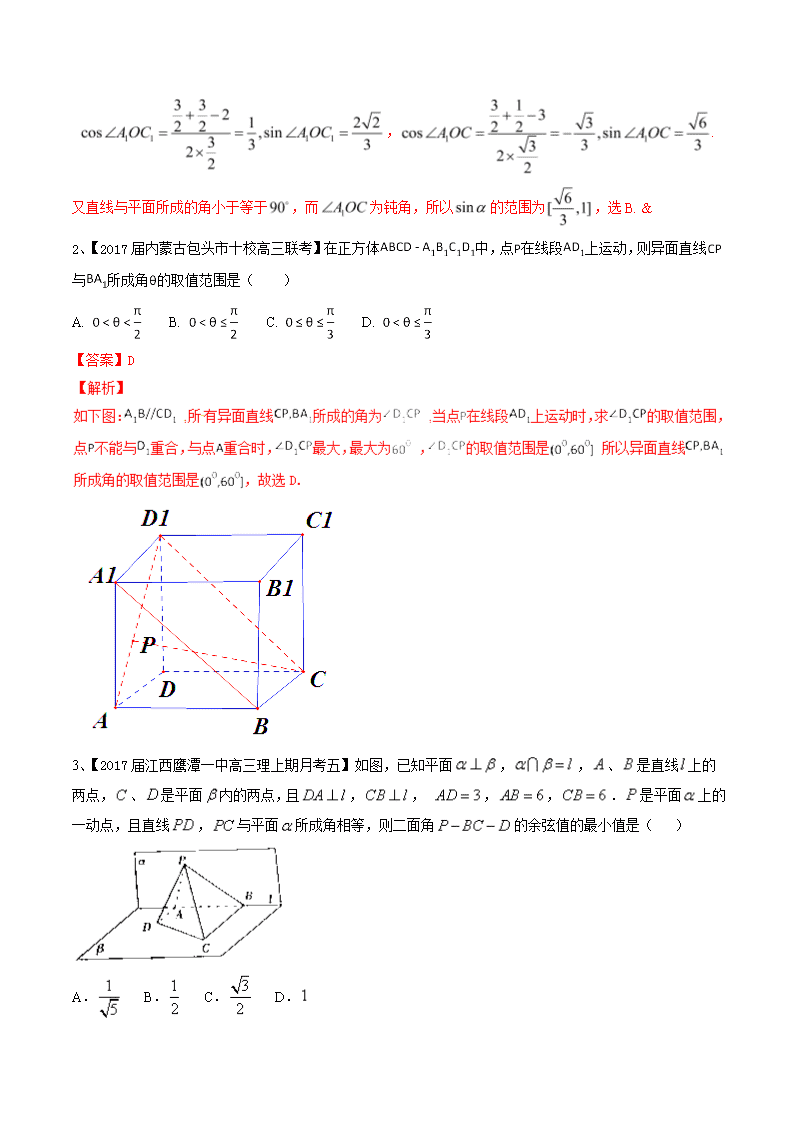‎ ‎【举一反三】‎ ‎1、【2014四川，理8】如图，在正方体中，点为线段的中点.设点在线段上，直线与平面所成的角为，则的取值范围是（）‎ A． B． C． D．‎ ‎【答案】B ‎ ，.‎ 又直线与平面所成的角小于等于，而为钝角，所以的范围为，选B. &‎ ‎2、【2017届内蒙古包头市十校高三联考】在正方体中，点在线段上运动，则异面直线与所成角的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎ ‎ ‎3、【2017届江西鹰潭一中高三理上期月考五】如图，已知平面，，、是直线上的两点，、是平面内的两点，且，， ，，．是平面上的一动点，且直线，与平面所成角相等，则二面角的余弦值的最小值是（ ）‎ A． B． C． D．‎ ‎【答案】C 类型二 立体几何中动态问题中的距离问题 ‎【例2】如图所示，在空间直角坐标系中，是坐标原点，有一棱长为的正方体，和分别是体对角线和棱上的动点，则的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】B&‎ ‎【指点迷津】求两点间的距离或其最值。一种方法，可建立坐标系，设点的坐标，用两点间距离公式写出距离，转化为求函数的最值问题；另一种方法，几何法，根据几何图形的特点，寻找那两点间的距离最大（小），求其值。‎ ‎【举一反三】‎ ‎1、【2016届湖南省长沙市长郡中高三下第六次月考】如图，已知正方体棱长为4，点在棱上，且，在侧面内作边长为1的正方形，是侧面内一动点，且点到平面距离等于线段的长，则当点运动时，的最小值是（ ）‎ A．21 B．22 C．23 D．25‎ ‎【答案】B ‎【解析】在上取点，使得，则面，连结，则．在平面上，以所在直线为轴，以所在直线为轴，由题意可知，点轨迹为抛物线，其方程为，点坐标为，设，则（其中，当时，，故．&2、如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.‎ ‎【答案】 ‎ ‎3、【2017届浙江省温州市高三第二次模拟考试】如图，在三棱锥中，平面平面，与均为等腰直角三角形，且，．点是线段上的动点，若线段上存在点，使得异面直线与成的角，则线段长的取值范围是（ ）‎ ‎ ‎ A. B. C. D. ‎ ‎【答案】B 类型三 立体几何中动态问题中的面积、体积问题 ‎【例3】在棱长为6的正方体中，是中点，点是面所在的平面内的动点，且满足，则三棱锥的体积最大值是（ ）‎ A. 36 B. C. 24 D. ‎ ‎【答案】B ‎【指点迷津】求几何体体积的最值，先观察几何图形三棱锥，其底面的面积为不变的几何量，求点P到平面BCD的距离的最大值，选择公式，可求最值。&‎