2012年数学福建省高考压轴卷 11页

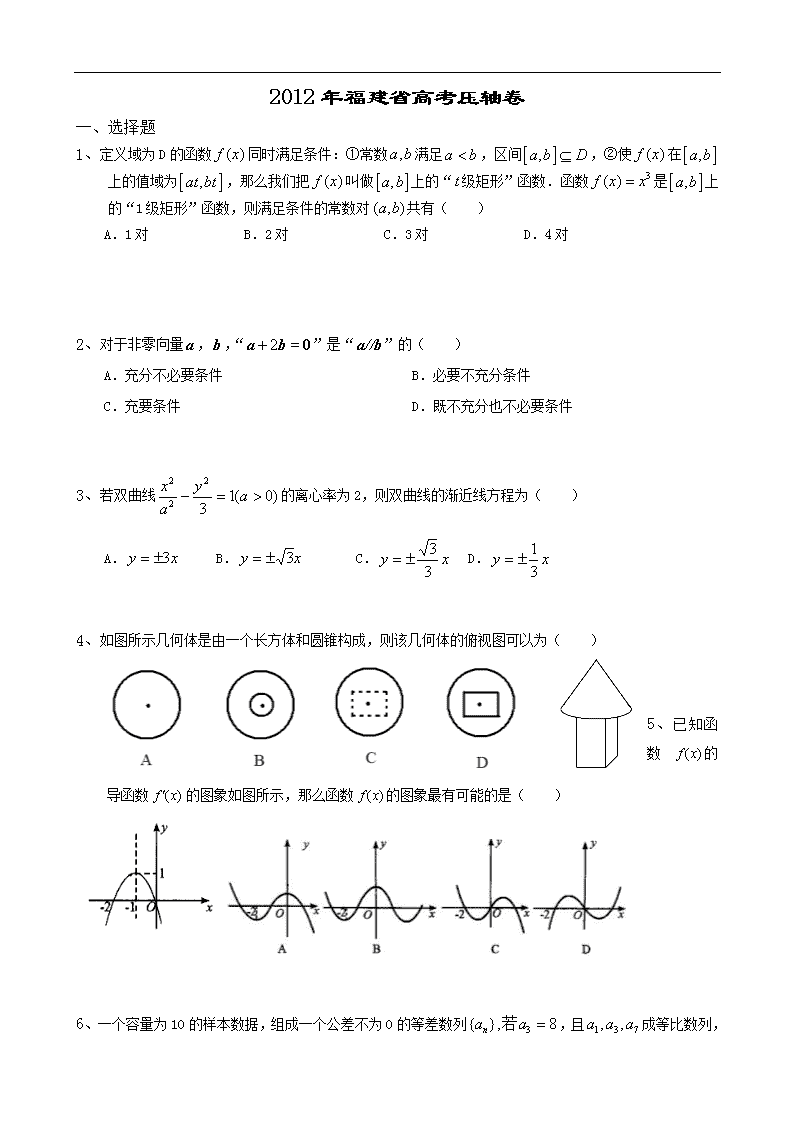
‎2012年福建省高考压轴卷 ‎ 一、选择题 ‎1、定义域为D的函数同时满足条件：①常数满足，区间，②使在上的值域为，那么我们把叫做上的“级矩形”函数．函数是上的“1级矩形”函数，则满足条件的常数对共有（ ）‎ A．1对 B．2对 C．3对 D．4对 ‎2、对于非零向量，，“”是“”的（ ）‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎3、若双曲线的离心率为2，则双曲线的渐近线方程为（ ）‎ A． B． C． D．‎ ‎4、如图所示几何体是由一个长方体和圆锥构成，则该几何体的俯视图可以为（ ）‎ ‎5、已知函数的导函数的图象如图所示，那么函数的图象最有可能的是（ ）‎ ‎6、一个容量为10的样本数据，组成一个公差不为0的等差数列，且 成等比数列，则此样本的平均数和中位数分别是（ ）‎ ‎ A．13，14 B．13，‎12 ‎C．12，13 D．13，13‎ ‎7、直线相切于点，则的值为 （ ）‎ ‎ A． B． C． D．‎ ‎8、若实数满足，则的最小值为（ ）‎ A． B．‎4 C．16 D．36‎ ‎9、将函数的图象向左平移个单位得到的图象关于轴对称，则的值可以为（ ）‎ A． B． C． D．‎ ‎10、设，集合，，则下列结论正确的是（ ）‎ A． B．‎ C． D．‎ ‎11、已知偶函数在区间单调递增，则满足＜的取值范围是（ ）‎ A．［，1） B．（，1） C．［0，1） D．（0，1）‎ ‎12、设、、是三个不同的平面，a、b是两条不同的直线，下列四个命题中正确的是（ ）‎ A．若，则 B．若，则 ‎ C．若，则 D．若在平面内的射影互相垂直，则 二、填空题 ‎13、已知，且为纯虚数，则 。‎ ‎14、平面上有一组平行线，且相邻平行线间的距离为‎3cm，把一枚半径为‎1cm 的硬币任意平掷在这个平面上，则硬币不与任何一条平行线相碰的概率为 。‎ ‎15、若直线与圆相切，则的值为 。‎ ‎16、某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮；现按同样的规律刺绣(小正方形的摆放规律相同)，设第个图形包含个小正方形，则 。 ‎ 三、解答题 ‎17、‎ 已知函数。‎ ‎（Ⅰ）求函数的单调区间。‎ ‎（Ⅱ）若上恒成立，求实数的取值范围 ‎（Ⅲ）在（Ⅱ）的条件下，对任意的，求证：。‎ ‎18、已知函数的一系列对应值如下表：‎ ‎ ‎ ‎（Ⅰ）求的解析式；‎ ‎（Ⅱ）若在中，，，，求∠B的值（答案也要修改）‎ ‎19、‎ 国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：‎ 序号()‎ 每天睡眠时间 ‎（小时）‎ 组中值()‎ 频数 频率 ‎()‎ ‎1‎ ‎[4，5)‎ ‎4．5‎ ‎8‎ ‎0．04‎ ‎2‎ ‎[5，6)‎ ‎5．5‎ ‎52‎ ‎0．26‎ ‎3‎ ‎[6，7)‎ ‎6．5‎ ‎60‎ ‎0．30‎ ‎4‎ ‎[7，8)‎ ‎7．5‎ ‎56‎ ‎0．28‎ ‎5‎ ‎[8，9)‎ ‎8．5‎ ‎20‎ ‎0．10‎ ‎6‎ ‎[9，10)‎ ‎9．5‎ ‎4‎ ‎0．02‎ ‎（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少?‎ ‎（Ⅱ）该网站利用右边的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义。‎ ‎20、如图一所示，边长为1的正方体中，分别为的中点。‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若为的中点，证明：；‎ ‎（Ⅲ）如图二所示为一几何体的展开图，沿着图中虚线将它们折叠起来，所得几何体的体积为，若正方体的体积为，求的值。‎ ‎21、若数列满足，其中为常数，则称数列为等方差数列 已知等方差数列满足。‎ ‎ （Ⅰ）求数列的通项公式；‎ ‎ （Ⅱ）记，则当实数大于4时，不等式能否对于一切的恒成立？请说明理由 ‎22、‎ 已知椭圆C：的短轴长为，且斜率为的直线过椭圆C的焦点及点。‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）已知一直线过椭圆C的左焦点，交椭圆于点P、Q，‎ ‎（ⅰ）若满足（为坐标原点），求的面积；‎ ‎（ⅱ）若直线与两坐标轴都不垂直，点M在轴上，且使为的一条角平分线，则称点M为椭圆C的“左特征点”，求椭圆C的左特征点。‎ 以下是答案 一、选择题 ‎1、 C ‎ ‎2、 A ‎3、 B ‎4、 C ‎5、 A ‎6、 D ‎7、 D ‎8、 C ‎9、 B ‎10、 A ‎11、 D ‎12、 B 二、填空题 ‎13、 ‎ ‎14、 ‎ ‎15、 ‎ ‎16、61‎ 三、解答题 ‎17、解：（Ⅰ）‎ 当时，恒成立，则函数在上单调递增；‎ 当时，由，则 ‎ 则在上单调递增，在上单调递减．　　 ‎ ‎（Ⅱ）由（Ⅰ）得：当时显然不成立；　　　　　　　　　　　　‎ ‎ 当时，,‎ 只需即可　．　　　　　　　　　　　　　　‎ 令,‎ 则，函数在上单调递减，在上单调递增．‎ ‎，‎ 即对恒成立，也就是对恒成立，‎ ‎∴解得，‎ ‎∴若在上恒成立，=1． ‎ ‎(Ⅲ）,　‎ 由得,‎ 由（Ⅱ）得： ,‎ 则,‎ 则原不等式成立　．　　　　‎ ‎ ‎ ‎18、解：（Ⅰ）由表格可知，函数的周期为，‎ 所以． ‎ 又，也即（公式中2kπ改为kπ），‎ 由，所以 ‎ 所以函数的解析式为（或者）‎ ‎（Ⅱ）∵，∴,‎ 在中，由正弦定理得， ‎ ‎∴，‎ ‎∵，∴，∴‎ ‎19、解:（Ⅰ）由样本数据可知，每天睡眠时间小于8小时的频率是 ‎． ‎ 由此估计每天睡眠时间小于8小时的学生约占88%． ‎ ‎（Ⅱ）输入的值后，由赋值语句可知，‎ 流程图进入一个求和状态．‎ 设，数列的前项和为，则 ‎．‎ 故输出的S值为6．7． ‎ S的统计意义是指被调查者每天的平均睡眠时间估计为6．7小时． ‎ ‎20、（Ⅰ）证明：取的中点，连接，，‎ ‎∵F、H分别是的中点，‎ ‎∴且，‎ ‎∵在正方体中，，‎ 又分别为的中点，‎ ‎∴，‎ ‎∴四边形FHBE为平行四边形，‎ ‎∴，‎ 又∵，‎ ‎∴；‎ ‎（Ⅱ）证明：取BC中点I，连接GI，AI，‎ 在正方形ABCD中，E，I分别为AB，BC的中点，‎ ‎∴，‎ ‎∵‎ ‎∴，‎ 又，‎ ‎∴，又，‎ ‎∴‎ 由四边形为平行四边形得，‎ ‎∴；‎ ‎（Ⅲ）如图二所示，该几何体为有一条侧棱垂直于底面且底面为正方形的四棱锥，即四棱锥的高为1，底面是边长为1的正方形， ‎ ‎∴，又， ‎ ‎∴．‎ ‎21、解：（Ⅰ）由，得，，．‎ ‎， ‎ ‎，，‎ 数列的通项公式为；‎ ‎（Ⅱ）解法一：，不等式恒成立，‎ 即对于一切的恒成立． ‎ 设． ‎ 当时，由于对称轴，且 而函数在是增函数，‎ 不等式恒成立，‎ 即当时，不等式对于一切的恒成立． ‎ 解法二：，不等式恒成立，‎ 即对于一切的恒成立． ‎ ‎，‎ 而 恒成立．‎ 故当时，不等式对于一切的恒成立． ‎ ‎22、解：（Ⅰ）由题意可知，直线的方程为 ‎∵直线过椭圆C的焦点，∴该焦点坐标为∴,‎ 又椭圆C的短轴长为，∴，∴，‎ ‎∴椭圆C的方程为；‎ ‎（Ⅱ）（ⅰ）∵，‎ ‎∴，‎ ‎∴，‎ ‎（ⅱ）设左特征点，左焦点为，可设直线PQ的方程为，‎ 由消去得，‎ 设则，‎ ‎∵为的一条角平分线，‎ ‎∴，即，‎ 又，，代入上式可得 ‎∴，‎ 解得，‎ ‎∴椭圆C的左特征点为．‎