湖北省金字三角2020届高三下学期3月线上联考数学（理）试题 Word版含解析 23页

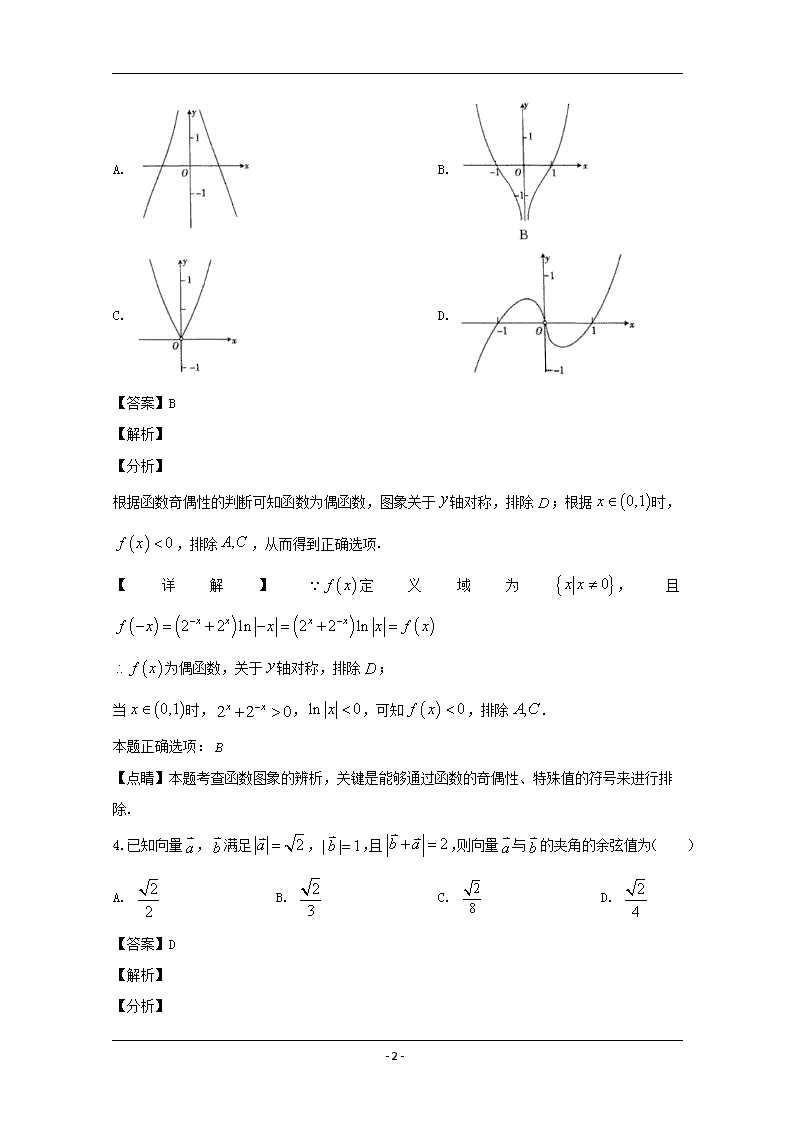
- 1 - 高三数学试卷（理科） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项 是符合题目要求的. 1.设 ，则 （ ） A. B. C. D. 【答案】C 【解析】 【分析】 根据复数运算法则求得 ，根据模长的定义求得结果. 【详解】 本题正确选项： 【点睛】本题考查复数模长的求解问题，关键是能够通过复数的运算求得复数，属于基础题. 2.已知集合 ， ，则 （ ） A. B. C. D. 【答案】A 【解析】 【分析】 分别求解出集合 和集合 ，根据交集 定义求得结果. 【详解】 ， 本题正确选项： 【点睛】本题考查集合运算中 交集运算，属于基础题. 3.函数 的图象大致为（ ） 的 的 3 5 1 iz ii = ++ z = 2 1 2 2 2 10 2 1 1 2 2z i= − + ( )3 5 1 1 1 1 2 2 2 i iiz i i ii − −= + = + = − ++ 1 1 2 4 4 2z∴ = + = C { }2 6 7 0A x x x= − − < { }B x x x= = − A B = ( ]1,0− ( ]7,0− [ )0,7 [ )0,1 A B { } ( )2 6 7 0 1,7A x x x= − − < = − { } ( ],0B x x x= = − = −∞ ( ]1,0A B∴ = − A ( )( ) 2 2 lnx xf x x−= + - 2 - A. B. C. D. 【答案】B 【解析】 【分析】 根据函数奇偶性的判断可知函数为偶函数，图象关于 轴对称，排除 ；根据 时， ，排除 ，从而得到正确选项. 【 详 解 】 定 义 域 为 ， 且 为偶函数，关于 轴对称，排除 ； 当 时， ， ，可知 ，排除 . 本题正确选项： 【点睛】本题考查函数图象的辨析，关键是能够通过函数的奇偶性、特殊值的符号来进行排 除. 4.已知向量 ， 满足 ， ，且 ，则向量 与 的夹角的余弦值为（ ） A. B. C. D. 【答案】D 【解析】 【分析】 y D ( )0,1x∈ ( ) 0f x < ,A C ( )f x { }0x x ≠ ( ) ( ) ( ) ( )2 2 ln 2 2 lnx x x xf x x x f x− −− = + − = + = ( )f x∴ y D ( )0,1x∈ 2 2 0x x−+ > ln 0x < ( ) 0f x < ,A C B a b 2a = | | 1b = 2b a+ =  a b 2 2 2 3 2 8 2 4 - 3 - 根据平方运算可求得 ，利用 求得结果. 【详解】由题意可知： ，解得： 本题正确选项： 【点睛】本题考查向量夹角的求解问题，关键是能够通过平方运算求得向量的数量积. 5.已知抛物线 ： 的准线 与圆 ： 相切，则 （ ） A. B. C. D. 【答案】D 【解析】 【分析】 先由抛物线方程得到准线方程，再由准线与圆相切，即可得出结果. 【详解】因为抛物线 的准线为 ， 又准线 与圆 相切， 所以 ，则 . 故选 D 【点睛】本题考查抛物线与圆的几何性质，熟记抛物线与圆的性质即可，属于常考题型. 6.已知等比数列 的前 项和为 ，若 ， ，则 （ ） A. 10 B. 7 C. 8 D. 4 【答案】C 【解析】 【分析】 根据等比数列的性质可将已知等式变为 ，解方程求得结果. 【详解】由题意得： 1 2a b⋅ = cos , a ba b a b ⋅< >=   2 2 22 3 2 4b a b a b a a b+ = + ⋅ + = + ⋅ =      1 2a b⋅ = 1 2cos , 42 2 a ba b a b ⋅∴ < >= = =   D C 2 2 ( 0)x py p= > l M 2 2( 1) ( 2) 16x y− + − = p = 6 8 3 4 2: 2C x py= 2 py = − l ( ) ( )2 2: 1 2 16M x y− + − = 2 42 p + = 4p = { }na n nS 1 2 3 1 1 1 2a a a + + = 2 2a = 3S = 1 2 3 3 2 2 24 a a a S a + + = = 1 3 1 2 3 3 2 1 2 3 1 3 2 2 1 1 1 1 24 a a a a a S a a a a a a a + + ++ + = + = = = 3 8S∴ = - 4 - 本题正确选项： 【点睛】本题考查等比数列性质的应用，关键是能够根据下角标的关系凑出关于 的方程， 属于基础题. 7.“割圆术”是刘徽最突出的数学成就之一，他在《九章算术注》中提出割圆术，并作为计 算圆的周长、面积以及圆周率的基础.刘徽把圆内接正多边形的面积一直算到了正 3072 边形， 并由此而求得了圆周率为 3.1415 和 3.1416 这两个近似数值，这个结果是当时世界上圆周率 计算的最精确数据.如图，当分割到圆内接正六边形时，某同学利用计算机随机模拟法向圆内 随机投掷点，计算得出该点落在正六边形内的频率为 0.8269，那么通过该实验计算出来的圆 周率近似值为（ ）（参考数据： ） A. 3.1419 B. 3.1417 C. 3.1415 D. 3.1413 【答案】A 【解析】 【分析】 先设圆的半径为 ，表示出圆的面积和正六边形的面积，再由题中所给概率，即可得出结果. 【详解】设圆的半径为 ，则圆的面积为 ，正六边形的面积为 ， 因而所求该实验的概率为 ，则 . 故选 A 【点睛】本题主要考查与面积有关的几何概型，熟记概率计算公式即可，属于常考题型. 8.已知函数 的最小正周期为 ，且对 ， 恒成立， 若函数 在 上单调递减，则 的最大值是（ ） C 3S 3 2.09460.8269 ≈ r r 2rπ 21 3 3 36 2 2 2r r r× × × = 2 2 3 3 3 32 0.82692 r rπ π= = 3 3 3.14192 0.8269 π = ≈× ( ) cos( )( 0)f x xω ϕ ω= + > π x∈R ( ) 3f x f π     ( )y f x= [0, ]a a - 5 - A. B. C. D. 【答案】B 【解析】 【分析】 先由最小正周期，求出 ，再由对 ， 恒成立，得到 ，进而可得 ，求出其单调递减区间，即可得出结果. 【详解】因为函数 的最小正周期为 ，所以 ， 又对任意的 ，都使得 ， 所以函数 在 上取得最小值，则 ， ， 即 ， 所以 ， 令 ，解得 ， 则函数 在 上单调递减，故 的最大值是 . 故选 B 【点睛】本题考查三角函数的图象及其性质，考查运算求解能力. 9.已知函数 ，设 ， ， ，则 ， ， 的大小关系为（ ） A. B. C. D. 【答案】C 【解析】 【分析】 先由函数奇偶性的概念判断函数 的奇偶性，再得到其单调性，确定 ， ， π 6 π 3 2π 3 5π 6 ω x∈R ( ) 3f x f π ≥    2 ,3 k k Z πϕ π= + ∈ ( ) cos 2 3f x x π = +   ( ) ( )cosf x xω ϕ= + π 2 2 πω π= = x ( ) 3f x f π ≥    ( )f x 3x π= 2 23 k π ϕ π π+ = + k Z∈ 2 ,3 k k Z πϕ π= + ∈ ( ) cos 2 3f x x π = +   2 2 2 ,3k x k k Z ππ π π≤ + ≤ + ∈ ,6 3k x k k Z π ππ π− + ≤ ≤ + ∈ ( )y f x= 0, 3 π     a 3 π | | 2( ) 2 xf x x= + 2 1(log )3m f= 0.1(7 )n f −= ( )4log 25p f= m n p m p n> > p n m> > p m n> > n p m> > ( )f x 2 1log 3 0.17 − - 6 - 的范围，即可得出结果. 【详解】因为 ，所以 ， 因此 为偶函数，且易知函数 在 上单调递增， 又 ， ， ， 所以 ， 因此 . 故选 C 【点睛】本题主要考查函数的奇偶性与单调性的应用，熟记函数性质即可，属于常考题型. 10.已知双曲线 的左、右焦点分别为 ， ，过 且斜率为 的直线 与双曲线在第一象限的交点为 ，若 ，则此双曲线的标准方程可能为（ ） A. B. C. D. 【答案】D 【解析】 【分析】 先 由 得 到 ， 根 据 的 斜 率 为 ， 求 出 ，结合余弦定理，与双曲线的定义，得到 ，求出 ，进而可得出结果. 【详解】由 ，可知 ， 又 的斜率为 ，所以易得 ， 在 中，由余弦定理得 ， 由双曲线的定义得 ， 4log 25 ( ) 22 xf x x= + ( ) 2 22 ( ) 2 ( )x xf x x x f x−− = + − = + = ( ) 22 xf x x= + ( )f x ( )0, ∞+ ( )2 2 1log log 3 1,23 = ∈ ( )0.17 0,1− ∈ ( )4 2log 25 log 5 2,3= ∈ 0.1 4 2 1log 25 log 73 −> > p m n> > 2 2 2 2 1( 0, 0)x y a ba b − = > > 1F 2F 2F 24 7 A ( )2 1 2 1 0F F F A F A+ ⋅ =   2 2 14 3 x y− = 2 2 13 4 x y− = 2 2 116 9 x y− = 2 2 19 16 x y− = ( )2 1 2 1 0F F F A F A+ ⋅ =   1 2 2 2FF F A c= = 2AF 24 7 2 1 7cos 25AF F∠ = − c a a b ( )2 1 2 1 0F F F A F A+ ⋅ =   1 2 2 2FF F A c= = 2AF 24 7 2 1 7cos 25AF F∠ = − 1 2AF F∆ 1 16 5AF c= 16 2 25 c c a− = - 7 - 所以 ，则 ， 所以此双曲线的标准方程可能为 . 故选 D 【点睛】本题考查双曲线的标准方程，熟记双曲线的几何性质与标准方程即可，属于常考题 型. 11.如图，在棱长为 2 的正方体 中，点 是 的中点，动点 在底面 内（不包括边界），若 平面 ，则 的最小值是（ ） A. B. C. D. 【答案】B 【解析】 【分析】 在 上取中点 ，在 上取中点 ，连接 ，根据面面平行的判定定 理可知平面 平面 ，从而可得 的轨迹是 （不含 两点）；由垂直关 系可知当 时， 取得最小值；利用面积桥和勾股定理可求得最小值. 【详解】如图，在 上取中点 ，在 上取中点 ，连接 5 3 ce a = = : 3: 4a b = 2 2 19 16 x y− = 1 1 1 1ABCD A B C D− M AD P ABCD 1B P  1A BM 1C P 30 5 2 30 5 2 7 5 4 7 5 1 1A D Q BC N 1 1, , ,DN NB B Q QD 1 / /B QDN 1A BM P DN ,D N CP DN⊥ 1C P 1 1A D Q BC N 1 1, , ,DN NB B Q QD - 8 - ， 且 ， 平面 平面 ，则动点 的轨迹是 （不含 两点） 又 平面 ，则当 时， 取得最小值 此时， 本题正确选项： 【点睛】本题考查立体几何中动点轨迹及最值的求解问题，关键是能够通过面面平行关系得 到动点的轨迹，从而找到最值取得的点. 12.已知函数 的极值点为 ，函数 的零点为 ，函数 的最大值为 ，则（ ） A. B. C. D. 【答案】A 【解析】 【分析】 根据 在 上单调递增，且 ，可知导函数零点在区间 内 ， 即 的 极 值 点 ； 根 据 单 调 递 增 且 可 知 ；通过判断 ，结合 单调性可得 ；利用导数可求得 / /DN BM 1/ /DQ A M DN DQ D= 1BM A M M= ∴ 1 / /B QDN 1A BM P DN ,D N 1CC ⊥ ABCD CP DN⊥ 1C P 2 2 2 1 2 51 2 CP ×= = + 2 2 1 2 2 302 55 C P  ∴ ≥ + =   B ( ) 2 ln2 x xf x e x= + − 1x ( ) 2xg x e x= + − 2x ( ) ln 2 xh x x = 3x 1 2 3x x x> > 2 1 3x x x> > 3 1 2x x x> > 3 2 1x x x> > ( )f x′ ( )0, ∞+ 1 1 02 4f f   ′ ′⋅ <       1 1,4 2      ( )f x 1 1 1,4 2x  ∈   ( )g x 1 1 02 4g g   ⋅ <       2 1 1,4 2x  ∈   ( ) ( )1 2g x g x> ( )g x 1 2x x> - 9 - ，即 ，从而可得三者的大小关系. 【详解】 在 上单调递增 且 ， 且 函数 在 上单调递增 且 ， 又 且 单调递增 由 可得： ，即 本题正确选项： 【点睛】本题考查函数极值点、零点、最值的判断和求解问题，涉及到零点存在定理的应用， 易错点是判断 大小关系时，未结合 单调性判断出 ，造成求解困难. 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分.把答案填在答题卡中的横线上. 13.设 ， 满足约束条件 ，则 的最小值是________. 【答案】0 【解析】 【分析】 画出可行域，平移基准直线 到可行域边界的位置，由此求得目标函数的最小值. 【详解】画出可行域如下图所示，由图可知当 平移到过点 时， . ( )max 1 1 2 4h x e = < 3 1 4x < ( ) 1xf x e x x ′ = + − ( )0, ∞+ 1 21 3 02 2f e ′ = − >   1 41 15 04 4f e ′ = − <   1 1 1,4 2x  ∴ ∈   1 1 1 1 0xe x x + − =  ( ) 2xg x e x= + − ( )0, ∞+ 1 21 3 02 2g e  = − >   1 41 1 2 04 4g e  = + − <   2 1 1,4 2x  ∴ ∈   ( ) ( )1 1 1 1 1 2 1 1 1 12 2 2 0xg x e x x x g xx x  = + − = − + − = − > =    ( )g x 1 2x x∴ > ( ) 2 1 ln 2 xh x x −′ = ( ) ( )max 1 2h x h e e = = 3 1 1 2 4x e = < 1 2 3x x x∴ > > A 1 2,x x ( )g x ( ) ( )1 2g x g x> x y 2 0 2 0 2 6 0 x y x y − ≥  + ≥  + − ≤ z x y= + 0x y+ = : 0l x y+ = (2, 2)− min 0z = - 10 - 【点睛】本题考查线性规划问题，考查数形结合的数学思想以及运算求解能力. 14.某公司对 2019 年 1~4 月份的获利情况进行了数据统计，如下表所示： 月份 1 2 3 4 利润 /万元 5 6 6.5 8 利用线性回归分析思想，预测出 2019 年 8 月份的利润为 11.6 万元，则 关于 的线性回归方 程为________. 【答案】 . 【解析】 【分析】 先由题中数据求出 ， ，结合题意，列出方程组，求出 与 ，即可得出结果. 【详解】设线性回归方程为 ，因为 ， ， 由题意可得 ，解得 ， ， 即 . 故答案为 x y y x ˆ 0.95 4y x= + x y ˆb ˆa ˆˆ ˆy bx a= + 5 2x = 51 8y = 5 51ˆ 2 8 8 ˆ 11.6 ˆ ˆ b a b a  + =  + = ˆ 0.95b = ˆ 4a = ˆ 0.95 4y x= + ˆ 0.95 4y x= + - 11 - 【点睛】本题主要考查线性回归方程，熟记回归方程的特征即可，属于常考题型. 15.若一个圆柱的轴截面是面积为 4 的正方形，则该圆柱的外接球的表面积为_______. 【答案】 【解析】 【分析】 作出圆柱与其外接球的轴截面，结合题中数据，求出外接球半径，再由球的表面积公式，即 可得出结果. 【详解】作出圆柱与其外接球的轴截面如下： 设圆柱的底面圆半径为 ，则 ，所以轴截面的面积为 ，解得 ， 因此，该圆柱的外接球的半径 ， 所以球的表面积为 . 故答案为 【点睛】本题主要考查圆柱外接球的相关计算，熟记公式即可，属于常考题型. 16.数列 为 1，1，2，1，1，2，3，1，1，2，1，1，2，3，4，…，首先给出 ，接 着复制该项后，再添加其后继数 2，于是 ， ，然后再复制前面所有的项 1，1，2， 再添加 2 的后继数 3，于是 ， ， ， ，接下来再复制前面所有的项 1， 1，2，1，1，2，3，再添加 4，…，如此继续，则 ______. 【答案】1 【解析】 【分析】 .8π r 2BC r= ( )22 4ABCDS r= =正方形 1r = 2 22 2 22 2 BDR += = = ( )2 4 2 8S π π= = 8π { }na 1 1a = 2 1a = 3 2a = 4 1a = 5 1a = 6 2a = 7 3a = 2019a = - 12 - 根据数列构造方法可知： ，即 ；根据变化规律可得 ，从而得到结果. 【详解】由数列 的构造方法可知 ， ， ， ，可得： 即： 本题正确结果： 【点睛】本题考查根据数列的构造规律求解数列中的项，关键是能够根据构造特点得到数列 各项之间的关系，考查学生的归纳总结能力. 三、解答题：本大题共 6 小题，共 70 分.解答应写出文字说明，证明过程或演算步骤.第 17~21 题为必考题，每道试题考生都必须作答.第 22、23 题为选考题，考生根据要求作答. （一）必考题：共 60 分. 17.在 中，角 ， ， 所对的边分别为 ， ， ， . （1）求 的大小； （2）若 ， ，求 的面积. 【答案】(1) .(2) 【解析】 【分析】 （ 1 ） 先 由 正 弦 定 理 ， 将 化 为 ，结合余弦定理，即可求出角 ； （2）先求出 ，再由正弦定理求出 ，根据三角形面积公式，即可得出结果. 【详解】（1）因为 ， 2 1na n− = ( )2 1 1 2 1n n kka a k− + = ≤ < − 2019 2a a= { }na 1 1a = 3 2a = 7 3a = 15 4a = 2 1na n− = ( )2 1 1 2 1n n kka a k− + = ≤ < − 2019 996 485 230 103 40 9 2 1a a a a a a a a∴ = = = = = = = = 1 ABC∆ A B C a b c 2sin sinsin sin sinsin B Cb B c C a AA  + = +    A 2a = π 3B = ABC∆ 4A π= 3 3 4ABCS∆ += 2sin sinsin sin sinsin B Cb B c C a AA  + = +    2 2 2 bcb c a aa  + = +   A sinC b 2sin sinsin sin sinsin B Cb B c C a AA  + = +    - 13 - 由正弦定理可得： ， 即 ， 再由余弦定理可得 ，即 , 所以 ； （2）因为 ，所以 ， 由正弦定理 ，可得 . . 【点睛】本题主要考查解三角形，熟记正弦定理、余弦定理即可，属于常考题型. 18.如图，在直四棱柱 中，底面 是矩形， 与 交于点 E. . （1）证明： 平面 ； （2）求直线 与平面 所成角的正弦值. 【答案】（1）证明见解析；（2） ． 【解析】 【分析】 （1）证明 ， ，推出 平面 ，得到 ，证明 ，即可证明 平面 ； 2 2 2 bcb c a aa  + = +   2 2 2 2b c a bc+ − = 2 cos 2bc A bc= 2cos 2A = 4A π= 3B π= ( ) 6 2sin sin 4C A B += + = sin sin a b A B = 3b = 1 3 3sin2 4ABCS ab C∆ += = 1 1 1 1ABCD A B C D− ABCD 1A D 1AD 1 2 4AA AB AD= = = AE ⊥ ECD 1AC EAC 6 9 1AA CD⊥ CD AD⊥ CD ⊥ 1 1AA D D CD AE⊥ AE ED⊥ AE ⊥ ECD - 14 - （2）建立坐标系，求出平面的法向量，利用空间向量的数量积求解直线 与平面 所成 角的正弦值． 【详解】（1）证明：∵四棱柱 是直四棱柱， ∴ 平面 ，而 平面 ，则 ， 又 ， ， ∴ 平面 ，因为平面 ，∴ ， ∵ ， ， ∴ 是正方形，∴ ， 又 ，∴ 平面 . （2）解：建立如图所示的坐标系， 与 交于点 ， ， 则 ， ∴ ， ∴ ， 设平面 的法向量为 ，则 ，即 ， 不妨取 ， 则直线 与平面 所成角的正弦值为 ． 1AC EAC 1 1 1 1ABCD A B C D− 1AA ⊥ ABCD CD ⊂ ABCD 1AA CD⊥ CD AD⊥ 1AA AD A= CD ⊥ 1 1AA D D 1 1AA D D CD AE⊥ 1AA AD⊥ 1AA AD= 1 1AA D D AE ED⊥ CD ED D= AE ⊥ ECD 1A D 1AD E 1 2 4AA AD AB= = = ( ) ( ) ( ) ( )10,0,0 , 0,0,4 , 2,4,0 , 0,4,0A A C D ( )0,2,2E ( ) ( ) ( )1 2,4, 4 , 2,4,0 , 0,2,2AC AC AE= − = =   EAC ( ), ,n x y z= · 0 · 0 n AC n AE  =  =   2 4 0 2 2 0 x y y z + =  + = ( )2,1, 1n = − − 1AC EAC 4 4 4 4 6= 96 36 6 6 n AC n AC − + −= =      - 15 - 【点睛】本题主要考查直线与平面所成角的求法，考查直线与平面垂直的判断和性质，考查 推理能力与计算能力，属于中档题． 19.某工厂预购买软件服务，有如下两种方案： 方案一：软件服务公司每日收取工厂 元，对于提供的软件服务每次 元； 方案二：软件服务公司每日收取工厂 元，若每日软件服务不超过 次，不另外收费，若 超过 次，超过部分的软件服务每次收费标准为 元． （1）设日收费为 元，每天软件服务的次数为 ，试写出两种方案中 与 的函数关系式； （2）该工厂对过去 天的软件服务的次数进行了统计，得到如图所示的条形图，依据该统 计数据，把频率视为概率，从节约成本的角度考虑，从两个方案中选择一个，哪个方案更合 适？请说明理由． 【答案】(1) 方案一中: ,方案二： .(2) 从 节约成本的角度考虑，选择方案一. 【解析】 【分析】 （1）根据题中条件，建立等量关系，即可得出所需函数关系； （2）分别设两种方案的日收费为 ， ，由题中条形图，得到 ， 的分布列，求出对应 期望，比较大小，即可得出结果. 【详解】（1）由题可知，方案一中的日收费 与 的函数关系式为 方案二中的日收费 与 的函数关系式为 . （2）设方案一种的日收费为 ，由条形图可得 的分布列为 190 200 210 220 230 0.1 0.4 0.1 0.2 0.2 60 10 200 15 15 20 y x y x 100 10 60,y x x N= + ∈ 200, 15, 20 100, 15, x x Ny x x x N ≤ ∈=  − > ∈ X Y X Y y x 10 60,y x x N= + ∈ y x 200, 15, 20 100, 15, x x Ny x x x N ≤ ∈=  − > ∈ X X X P - 16 - 所以 （元） 方案二中的日收费为 ，由条形图可得 的分布列为 200 220 240 0.6 0.2 0.2 （元） 所以从节约成本的角度考虑，选择方案一. 【点睛】本题主要考查函数的应用，以及离散型随机变量的分布列与期望，熟记相关概念即 可，属于常考题型. 20.已知椭圆 ： 的离心率为 ，焦距为 . （1）求 方程； （2）若斜率为 的直线 与椭圆 交于 ， 两点（点 ， 均在第一象限）， 为坐标 原点. ①证明：直线 的斜率依次成等比数列. ②若 与 关于 轴对称，证明： . 【答案】（1） ； （2）①见解析；②见解析. 【解析】 【分析】 （1）根据离心率、焦距和 可解出 ，从而得到椭圆方程；（2）①设直线 的方程为： ， ， ，将直线方程与椭圆方程联立可得韦达定 理的形式，从而求得 ；整理可知： ，从而证得结论；② 与 关 于 轴 对 称 可 知 ， 由 ① 知 ， 则 的 ( ) 190 0.1 200 0.4 210 0.1 220 0.2 230 0.2 210E X = × + × + × + × + × = Y Y Y P ( ) 200 0.6 220 0.2 240 0.2 212E Y = × + × + × = C ( )2 2 2 2 1 0x y a ba b + = > > 3 2 2 3 C 1 2 − l C P Q P Q O , ,OP PQ OQ Q′ Q x 4tan 3POQ′∠ > 2 2 14 x y+ = 2 2 2b a c= − , ,a b c l 1 2y x m= − + ( )1 1,P x y ( )2 2,Q x y 1 2y y 21 2 1 2 1 4Q QO O PP y yk k kx x = = = Q′ Q x xOQ xOQ′∠ = ∠ 1tan tan 4xOQ xOP′∠ ⋅ ∠ = - 17 - ，利用两角和差正切公式展开整理，根据基本不等式求 得最小值，经验证等号无法取得，从而证得结论. 【详解】（1）由题意可得： ，解得： 椭圆 的方程为： （2）证明：①设直线 的方程为： ， ， 由 消去 得： 则 ，且 ， 即直线 的斜率依次成等比数列 ②由题可知： 由①可知： ， ， 若 ，则 两点重合，不符合题意；可知无法取得等号 【点睛】本题考查椭圆标准方程求解、直线与椭圆综合应用问题，涉及到斜率关系的证明和 不等式的证明.证明不等式的关键是能够利用倾斜角的关系，利用两角和差正切公式构造出符 ( )tan tanPOQ xOQ xOP′ ′∠ = ∠ + ∠ 3 2 2 2 3 c a c  =  = 2 3 a c = = 2 2 2 1b a c∴ = − = ∴ C 2 2 14 x y+ = l 1 2y x m= − + ( )1 1,P x y ( )2 2,Q x y 2 2 1 2 14 y x m x y  = − +  + = y ( )2 22 2 1 0x mx m− + − = ( ) ( )2 2 24 8 1 4 2 0m m m∆ = − − = − > 1 2 2x x m+ = ( )2 1 2 2 1x x m= − ( ) 2 2 1 2 1 2 1 2 1 2 1 1 1 1 1 2 2 4 2 2 my y x m x m x x m x x m −  ∴ = − + − + = − + + =     ( ) 2 21 2 2 1 2 1 12 42 1OP OQ PQ m y yk k kx x m − ∴ = = = = − , ,OP PQ OQ xOQ xOQ′∠ = ∠ 1tan tan 4xOQ xOP′∠ ⋅ ∠ = tan 0xOQ′∠ > tan 0xOP∠ > ( ) tan tantan tan 1 tan tan xOQ xOPPOQ xOQ xOP xOQ xOP ′∠ + ∠′ ′∴ ∠ = ∠ + ∠ = ′− ∠ ⋅ ∠ ( )4 4tan tan 2 tan tan3 3 4 3xOQ xOP xOQ xOP′ ′= ∠ + ∠ × ⋅ ∠ =≥ ∠ xOQ xOP′∠ = ∠ ,P Q 4tan 3POQ′∴ ∠ > - 18 - 合基本不等式的形式，利用基本不等式求得最值；易错点是忽略对于取等条件能否成立的验 证. 21.已知函数 ，曲线 在点 处的切线方程为 . （1）求函数 的解析式，并证明： . （2）已知 ，且函数 与函数 的图象交于 ， 两点， 且线段 的中点为 ，证明： . 【答案】（1） ，证明见解析； （2）证明见解析. 【解析】 【分析】 （1）利用切线方程可求得 的解析式，令 ，利用导数可 求得 ，从而证得结论；（2）通过分析法可知要证 成立只 需 证 ； 令 ， 即 证 ： ； 令 ，利用导数研究 单调性，可知 ，得到 成 立 ； 令 ， 利 用 导 数 研 究 单 调 性 ， 可 知 ， 得 到 成立，可知需证的不等式成立，则原不等式成立. 【详解】（1）由题意得： ，即 又 ，即 ，则 ，解得： 则 . 令 ， 令 ，解得： ( ) xf x e ax b= + + ( )y f x= ( )( )1, 1f 2 0ex y− − = ( )f x ( ) 1f x x≥ − ( ) 2g x kx= − ( )f x ( )g x ( )1 1,A x y ( )2 2,B x y AB ( )0 0,P x y ( ) ( )0 01f x g y< < ( ) 2xf x e= − ( )f x ( ) ( ) 1 1xh x f x x e x= − + = − − ( ) ( )0 0h x h≥ = ( ) ( )0 01f x g y< < 2 1 2 1 2 1 2 2 1 1 1 2 x x x x x xe e x xe − − −− +< <− 2 1 0t x x= − > 2 1 1 2 t t te ee t − +< < ( ) 2 2 t t F t e e t −= − − ( )F t ( ) ( )0 0F t F> = 2 1t tee t −< ( ) 1 1 2 t t e tG t e −= −+ ( )G t ( ) ( )0 0G t G< = 1 1 2 t te e t − +< ( )1 2f e a b e= + + = − 2a b+ = − ( ) xf x e a′ = + ( )1f e a e′ = + = 0a = 2b = − ( ) 2xf x e= − ( ) ( ) 1 1xh x f x x e x= − + = − − ( ) 1xh x e′ = − ( ) 0h x′ = 0x = - 19 - 则函数 在 上单调递减，在 上单调递增 ，则： （2）要证 成立，只需证： 即证 ，即： 只需证： 设 ，即证： 要证 ，只需证： 令 ，则 在 上为增函数 ，即 成立； 要证 ，只需证明： 令 ，则 在 上为减函数 ，即 成立 ， 成立 成立 【点睛】本题考查导数在研究函数中的应用，涉及到导数几何意义的应用、利用导数证明不 等式、分析法证明不等式的问题，关键是能够通过构造函数的方式，将所证不等式转变为函 ( )h x ( ),0−∞ ( )0, ∞+ ( ) ( )0 0h x h∴ ≥ = ( ) 1f x x≥ − ( ) ( )0 01f x g y< < 1 2 1 2x 2 42 2 2 x x xe ee k + + −− < − < 1 2 1 2 2 2 x x x xek ee + +< < 11 2 2 1 2 2 2 1 2 x x xxx xe ee x e e x + − +< <− 2 1 2 1 2 1 2 2 1 1 1 2 x x x x x xe e x xe − − −− +< <− 2 1 0t x x= − > 2 1 1 2 t t te ee t − +< < 2 1t tee t −< 2 2 t t e e t −− > ( ) 2 2 t t F t e e t −= − − ( ) 2 21 1 02 t t F t e e − ′ = + − >    ( )F t∴ ( )0, ∞+ ( ) ( )0 0F t F∴ > = 2 1t tee t −< 1 1 2 t te e t − +< 1 1 2 t t e t e − <+ ( ) 1 1 2 t t e tG t e −= −+ ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 4 1 12 1 021 2 1 2 1 t t tt t t t e e eeG t e e e − + − −′ = − = = < + + + ( )G t∴ ( )0, ∞+ ( ) ( )0 0G t G∴ < = 1 1 2 t te e t − +< 2 1 1 2 t t te ee t − +∴ < < 0t > ( ) ( )0 01f x g y∴ < < - 20 - 数最值的求解问题，构造合适的函数是解决本题的难点. （二）选考题：共 10 分.请考生在第 22，23 题中任选一题作答.如果多做，则按所做的第一 题计分. 选修 4-4：坐标系与参数方程 22.在直角坐标系 中，直线 的方程为 ，曲线 的参数方程为 （ 为参数）.以坐标原点为极点， 轴正半轴为极轴建立极坐标系. （1）求直线 和曲线 的极坐标方程； （2）若直线 与曲线 交于 ， 两点，且直线 与 的斜率之积为 ，求 . 【答案】（1） : ， ： ；（2） . 【解析】 【分析】 （1）利用直角坐标与极坐标换算公式直接可得； （2）联立直线 与曲线 的极坐标方程，得 ，设 ，则 ，解得 即可. 【详解】（1）将 ， 代入 的方程中，所以直线 的极坐标 方程为 . 在曲线 的参数方程中，消去 ，可得 ，将 ， 代入 的方程中， 所以曲线 的极坐标方程为 . （2）直线 与曲线 的公共点的极坐标满足方程组 ，由方程组得 ， ，两边同除 ， 可化为 ，即 ， xOy l 0x y a+ − = C 2cos , sin x y α α =  = α x l C l C A B OA OB 5 4 a l cos sin 0ar q r q+ - = C ( )2 2 24sin cos 4ρ θ θ+ = 1 2a = ± l C ( ) ( )2 2 224sin cos 4 cos sina θ θ θ θ++ = ( ) ( )1 1 2 2, , ,A Bρ θ ρ θ 1 2 5tan tan 4OO BAk k θ θ= = a cosx ρ θ= siny ρ θ= 0x y a+ − = l cos sin 0ar q r q+ - = C α 2 2 14 x y+ = cosx ρ θ= siny ρ θ= 2 2 14 x y+ = C ( )2 2 24sin cos 4ρ θ θ+ = l C ( )2 2 2 cos sin 0 4sin cos 4 aρ θ ρ θ ρ θ θ + − = + = ( ) ( )2 2 224sin cos 4 cos sina θ θ θ θ++ = ( )2 2 2 2 2 24 sin cos 4 si 2cosn sincosa aθ θθ θ θ θ+ = + + 2cos θ 2 2 2 24 tan 4 8tan 4tana aθ θ θ+ = + + ( )2 2 24 4 tan 8tan 4 0a aθ θ− − + − = - 21 - 设 ，则 ， 解得 . 【点睛】本题考查了参数方程，极坐标方程，普通方程之间的换算关系．考查了直线与椭圆 极坐标方程的应用．属于中档题． 选修 4-5：不等式选讲 23.已知函数 . （1）求不等式 的解集； （2）若 ，使得 恒成立，求 的取值范围. 【答案】(1) (2) . 【解析】 【分析】 （1）先由题意得 ，再分别讨论 ， ， 三种情况，即 可得出结果； （2）先由含绝对值不等式的性质，得到 ，再由题 意，可得 ，求解，即可得出结果. 【详解】（1）不等式 可化为 ， 当 时， ， ，所以无解； 当 时， 所以 ； 当 时， ， ，所以 ， 综上，不等式 的解集是 . （2）因为 又 ，使得 恒成立，则 ， ，解得 . . ( ) ( )1 1 2 2, , ,A Bρ θ ρ θ 2 1 2 2 4 5tan tan 4 4 4O OBA ak k a θ θ −= = =− 1 2a = ± ( ) | 2 |f x x= + ( ) ( 2) 4f x f x x+ − < + x∀ ∈R ( ) ( ) (2 )f x a f x f a+ +  a { }2 2x x− < < 22, 3  − −   2 4x x x+ + < + 2x −≤ 2 0x− < ≤ 0x > ( ) ( ) 2 2f x a f x x a x a+ + = + + + + ≥ 2 2a a≥ + ( ) ( )2 4f x f x x+ − < + 2 4x x x+ + < + 2x −≤ 2 2 4x x− − < + 2x > − 2 0x− < ≤ 2 4x< + 2 0x− < ≤ 0x > 2 2 4x x+ < + 2x < 0 2x< < ( ) ( )2 4f x f x x+ − < + { }| 2 2x x− < < ( ) ( ) 2 2f x a f x x a x a+ + = + + + + ≥ x R∀ ∈ ( ) ( ) ( )2f x a f x f a+ + ≥ 2 2a a≥ + ( )22 2 2a a≥ + 22 3a− ≤ ≤ − - 22 - 所以 的取值范围为 . 【点睛】本题主要考查含绝对值的不等式，熟记分类讨论的思想，以及绝对值不等式的性质 即可，属于常考题型. a 22, 3  − −   - 23 -