【数学】2020届一轮复习人教A版 数学文化 作业 5页

‎【备战2018高考高三数全国各地一模试卷分项精品】‎ 专题十一 数文化 ‎【2018湖南衡阳上期期末】《九章算术》之后，人们会了用等差数列的知识来解决问题，《张丘建算经》卷上第22题为：“今有女善织，且益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，现一月（按30天计）共织390尺布”，则从第2天起每天比前一天多织布的尺数为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【点睛】本题考查等差数列的四项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．‎ ‎【2018山西五校联考】在我刚明代数家吴敬所著的《九章算术比类大全》中，有一道数命题叫“宝塔装灯”，内容为 “远望魏巍塔七层，红灯点点倍加增；共灯三百八十一，请问顶层几盏灯？”（“倍加增”指灯的数量从塔的顶层到底层按公比为的等比数列递增），根据此诗，可以得出塔的顶层和底层共有（ ）‎ A. 盏灯 B. 盏灯 C. 盏灯 D. 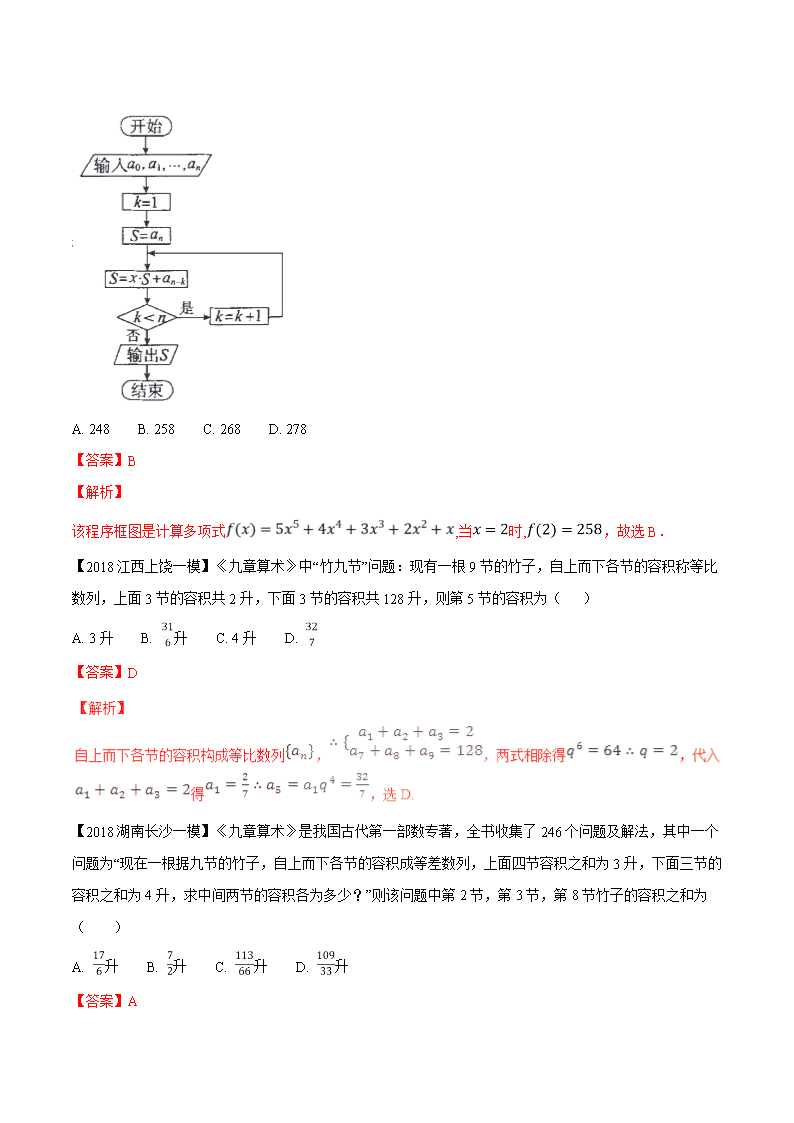盏灯 ‎【答案】C ‎【解析】‎ 设顶层的灯数为 ，公比为， ， ，解得 ，底层为 ，所以 盏灯，故选C.‎ ‎【2018云南师大附中月考】秦九韶算法是南宋时期数家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，其算法的程序框图如图所示，若输入的分别为，若，根据该算法计算当时多项式的值，则输出的结果为（ ）‎ ‎【备战2018高考高三数全国各地一模试卷分项精品】‎ 专题十一 数文化 ‎【2018湖南衡阳上期期末】《九章算术》之后，人们会了用等差数列的知识来解决问题，《张丘建算经》卷上第22题为：“今有女善织，且益功疾（注：从第2天开始，每天比前一天多织相同量的布），第一天织5尺布，现一月（按30天计）共织390尺布”，则从第2天起每天比前一天多织布的尺数为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【点睛】本题考查等差数列的四项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．‎ ‎【2018山西五校联考】在我刚明代数家吴敬所著的《九章算术比类大全》中，有一道数命题叫“宝塔装灯”，内容为 “远望魏巍塔七层，红灯点点倍加增；共灯三百八十一，请问顶层几盏灯？”（“倍加增”指灯的数量从塔的顶层到底层按公比为的等比数列递增），根据此诗，可以得出塔的顶层和底层共有（ ）‎ A. 盏灯 B. 盏灯 C. 盏灯 D. 盏灯 ‎【答案】C ‎【解析】‎ 设顶层的灯数为 ，公比为， ， ，解得 ，底层为 ，所以 盏灯，故选C.‎ ‎【2018云南师大附中月考】秦九韶算法是南宋时期数家秦九韶提出的一种多项式简化算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，即使在现代，它依然是利用计算机解决多项式问题的最优算法，其算法的程序框图如图所示，若输入的分别为，若，根据该算法计算当时多项式的值，则输出的结果为（ ）‎ A. 248 B. 258 C. 268 D. 278‎ ‎【答案】B ‎【解析】‎ 该程序框图是计算多项式,当时,，故选B．‎ ‎【2018江西上饶一模】《九章算术》中“竹九节”问题：现有一根9节的竹子，自上而下各节的容积称等比数列，上面3节的容积共2升，下面3节的容积共128升，则第5节的容积为（ ）‎ A. 3升 B. 升 C. 4升 D. ‎ ‎【答案】D ‎【2018湖南长沙一模】《九章算术》是我国古代第一部数专著，全书收集了246个问题及解法，其中一个问题为“现在一根据九节的竹子，自上而下各节的容积成等差数列，上面四节容积之和为3升，下面三节的容积之和为4升，求中间两节的容积各为多少？”则该问题中第2节，第3节，第8节竹子的容积之和为（ ）‎ A. 升 B. 升 C. 升 D. 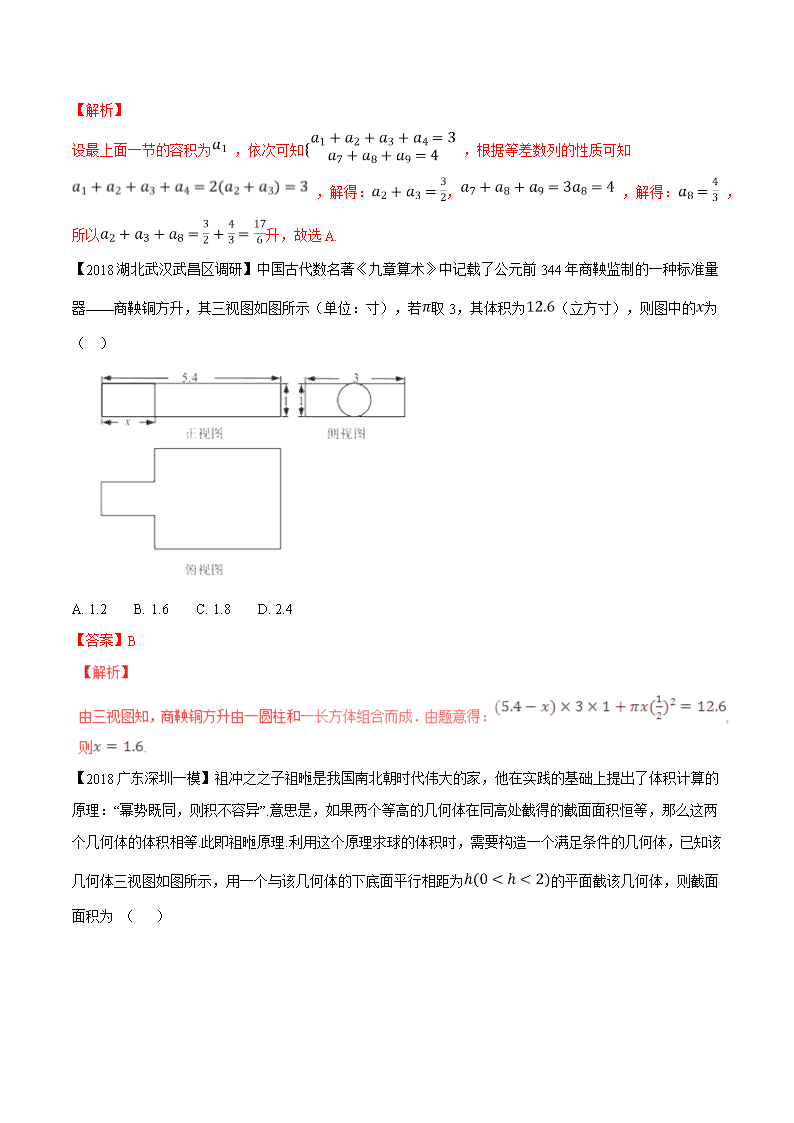升 ‎【答案】A ‎【解析】‎ 设最上面一节的容积为 ，依次可知 ，根据等差数列的性质可知 ，解得：， ，解得： ，所以升，故选A.‎ ‎【2018湖北武汉武昌区调研】中国古代数名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升，其三视图如图所示（单位：寸），若取3，其体积为（立方寸），则图中的为（ ）‎ A. 1.2‎‎ B. 1.6 C. 1.8 D. 2.4‎ ‎【答案】B ‎【2018广东深圳一模】祖冲之之子祖暅是我国南北朝时代伟大的家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”.意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为的平面截该几何体，则截面面积为 （ ）‎ A. B. C. D. ‎ ‎【答案】D