2020届二轮复习直线与平面垂直的判定教案（全国通用） 8页

‎2020届二轮复习 直线与平面垂直的判定 教案（全国通用）‎ 重点难点 教学重点:直线与平面垂直的判定.‎ 教学难点:灵活应用直线与平面垂直判定定理解决问题.‎ 课时安排 ‎ 1课时 教学过程 导入新课 思路1.(情境导入)‎ ‎ 日常生活中，我们对直线与平面垂直有很多感性认识，比如，旗杆与地面的位置关系，大桥的桥柱与水面的位置关系等，都给我们以直线与平面垂直的印象.‎ ‎ 在阳光下观察直立于地面的旗杆及它在地面的影子.随着时间的变化，尽管影子BC的位置在移动，但是旗杆AB所在直线始终与BC所在直线垂直.也就是说，旗杆AB所在直线与地面内任意一条不过点B的直线B′C′也是垂直的.‎ 思路2.(事例导入)‎ ‎ 如果一条直线垂直于一个平面的无数条直线，那么这条直线是否与这个平面垂直？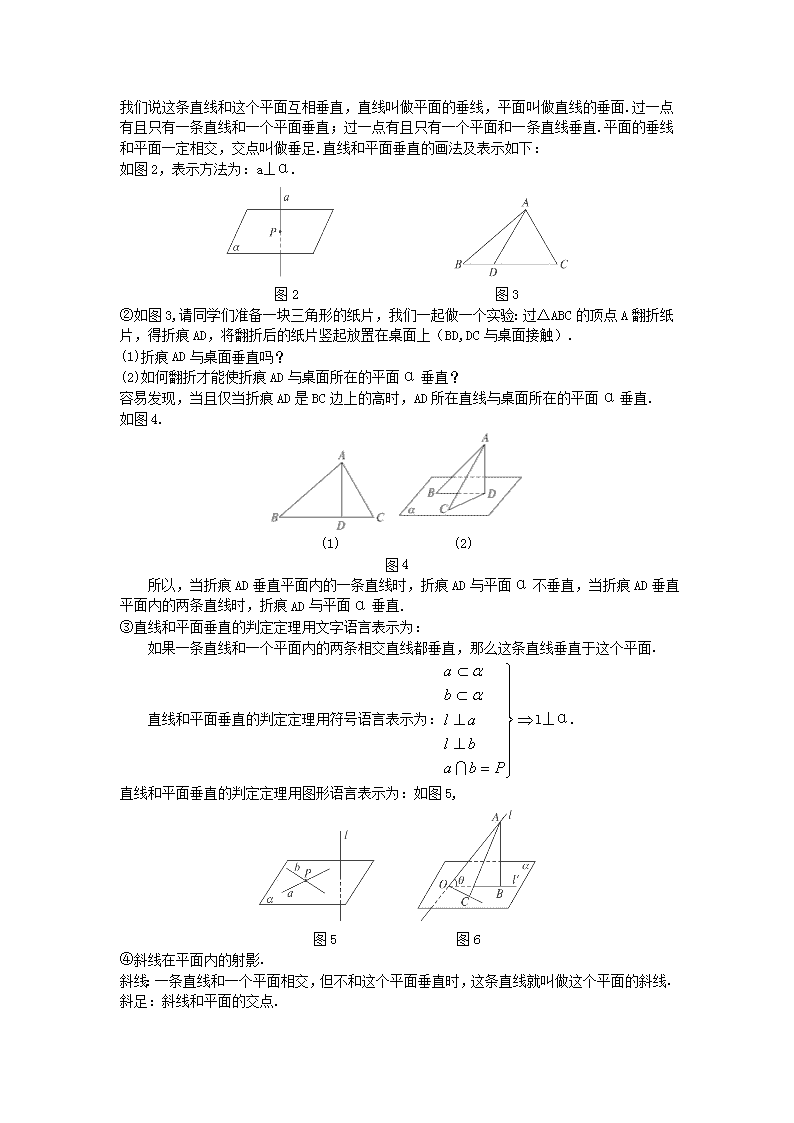举例说明.‎ ‎ 如图1，直线AC1与直线BD、EF、GH等无数条直线垂直，但直线AC1与平面ABCD不垂直.‎ 图1‎ 推进新课 新知探究 提出问题 ‎①探究直线与平面垂直的定义和画法.‎ ‎②探究直线与平面垂直的判定定理.‎ ‎③用三种语言描述直线与平面垂直的判定定理.‎ ‎④探究斜线在平面内的射影，讨论直线与平面所成的角.‎ ‎⑤探究点到平面的距离.‎ 活动:问题①引导学生结合事例观察探究.‎ 问题②引导学生结合事例实验探究.‎ 问题③引导学生进行语言转换.‎ 问题④引导学生思考其合理性.‎ 问题⑤引导学生回忆点到直线的距离得出点到平面的距离.‎ 讨论结果：①直线与平面垂直的定义和画法：‎ 教师演示实例并指出书脊（想象成一条直线）、各书页与桌面的交线，由于书脊和书页底边（即与桌面接触的一边）垂直，得出书脊和桌面上所有直线都垂直，书脊和桌面的位置关系给了我们直线和平面垂直的形象.从而引入概念：一条直线和平面内的任何一条直线都垂直，我们说这条直线和这个平面互相垂直，直线叫做平面的垂线，平面叫做直线的垂面.过一点有且只有一条直线和一个平面垂直；过一点有且只有一个平面和一条直线垂直.平面的垂线和平面一定相交，交点叫做垂足.直线和平面垂直的画法及表示如下：‎ 如图2，表示方法为：a⊥α.‎ ‎ ‎ 图2 图3‎ ‎②如图3,请同学们准备一块三角形的纸片，我们一起做一个实验：过△ABC的顶点A翻折纸片，得折痕AD，将翻折后的纸片竖起放置在桌面上（BD,DC与桌面接触）.‎ ‎(1)折痕AD与桌面垂直吗？‎ ‎(2)如何翻折才能使折痕AD与桌面所在的平面α垂直？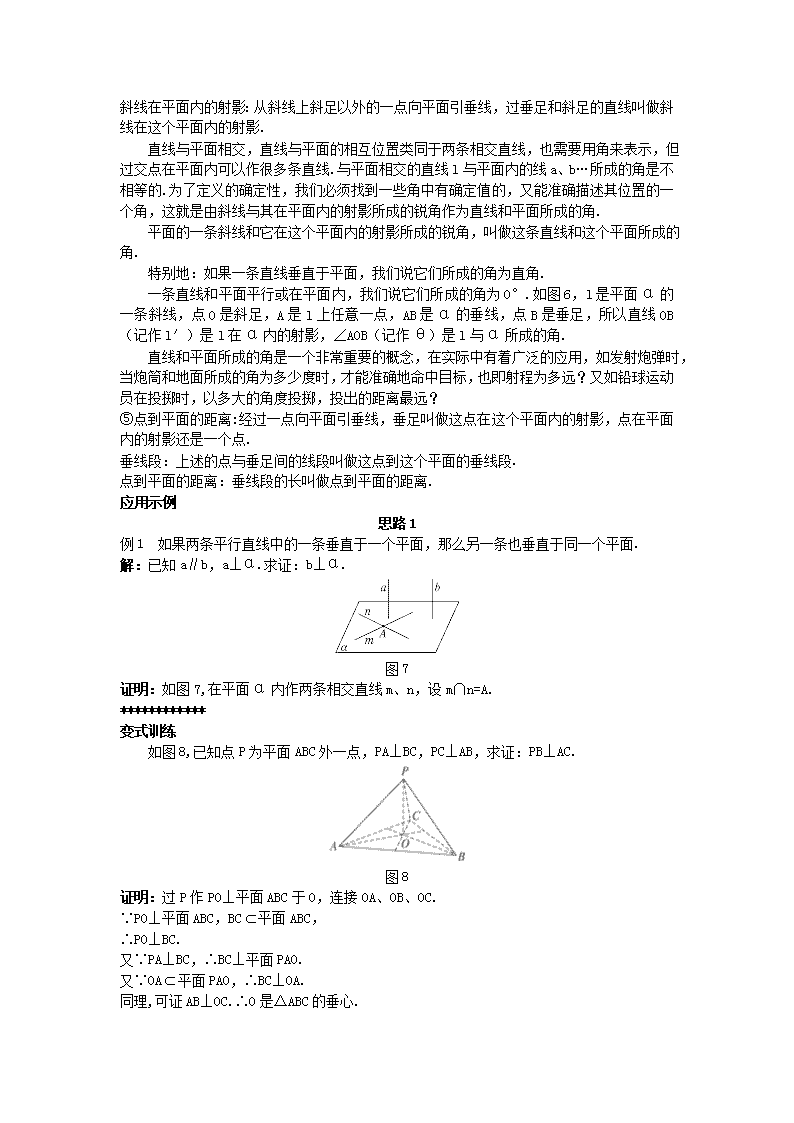‎ 容易发现，当且仅当折痕AD是BC边上的高时，AD所在直线与桌面所在的平面α垂直.‎ 如图4.‎ ‎(1) (2)‎ 图4‎ ‎ 所以，当折痕AD垂直平面内的一条直线时，折痕AD与平面α不垂直，当折痕AD垂直平面内的两条直线时，折痕AD与平面α垂直.‎ ‎③直线和平面垂直的判定定理用文字语言表示为：‎ ‎ 如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面.‎ ‎ 直线和平面垂直的判定定理用符号语言表示为：l⊥α.‎ 直线和平面垂直的判定定理用图形语言表示为：如图5,‎ ‎ ‎ 图5 图6‎ ‎④斜线在平面内的射影.‎ 斜线：一条直线和一个平面相交，但不和这个平面垂直时，这条直线就叫做这个平面的斜线.‎ 斜足：斜线和平面的交点.‎ 斜线在平面内的射影：从斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影.‎ ‎ 直线与平面相交，直线与平面的相互位置类同于两条相交直线，也需要用角来表示，但过交点在平面内可以作很多条直线.与平面相交的直线l与平面内的线a、b…所成的角是不相等的.为了定义的确定性，我们必须找到一些角中有确定值的，又能准确描述其位置的一个角，这就是由斜线与其在平面内的射影所成的锐角作为直线和平面所成的角.‎ ‎ 平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角.‎ ‎ 特别地：如果一条直线垂直于平面，我们说它们所成的角为直角.‎ ‎ 一条直线和平面平行或在平面内，我们说它们所成的角为0°.如图6，l是平面α的一条斜线，点O是斜足，A是l上任意一点，AB是α的垂线，点B是垂足，所以直线OB（记作l′）是l在α内的射影，∠AOB（记作θ）是l与α所成的角.‎ ‎ 直线和平面所成的角是一个非常重要的概念，在实际中有着广泛的应用，如发射炮弹时，当炮筒和地面所成的角为多少度时，才能准确地命中目标，也即射程为多远？又如铅球运动员在投掷时，以多大的角度投掷，投出的距离最远？‎ ‎⑤点到平面的距离:经过一点向平面引垂线，垂足叫做这点在这个平面内的射影，点在平面内的射影还是一个点.‎ 垂线段：上述的点与垂足间的线段叫做这点到这个平面的垂线段.‎ 点到平面的距离：垂线段的长叫做点到平面的距离.‎ 应用示例 思路1‎ 例1 如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面.‎ 解：已知a∥b，a⊥α.求证：b⊥α.‎ 图7‎ 证明：如图7,在平面α内作两条相交直线m、n，设m∩n=A.‎ ‎************‎ 变式训练 ‎ 如图8,已知点P为平面ABC外一点，PA⊥BC，PC⊥AB，求证：PB⊥AC.‎ 图8‎ 证明：过P作PO⊥平面ABC于O，连接OA、OB、OC.‎ ‎∵PO⊥平面ABC，BC平面ABC，‎ ‎∴PO⊥BC.‎ 又∵PA⊥BC，∴BC⊥平面PAO.‎ 又∵OA平面PAO，∴BC⊥OA.‎ 同理,可证AB⊥OC.∴O是△ABC的垂心.‎ ‎∴OB⊥AC.可证PO⊥AC.‎ ‎∴AC⊥平面PBO.‎ 又PB平面PBO，∴PB⊥AC.‎ 点评：欲证线面垂直需要转化为证明线线垂直，欲证线线垂直往往转化为线面垂直.用符号语言证明问题显得清晰、简洁.‎ 例2 如图9,在正方体ABCD—A1B1C1D1中，求直线A1B和平面A1B1CD所成的角.‎ 图9‎ 活动：先让学生思考或讨论后再回答，经教师提示、点拨，对回答正确的学生及时表扬，对回答不准确的学生提示引导考虑问题的思路.‎ 解：连接BC1交B1C于点O，连接A1O.‎ 设正方体的棱长为a，‎ 因为A1B1⊥B1C1,A1B1⊥B1B,所以A1B1⊥平面BCC1B1.‎ 所以A1B1⊥BC1.‎ 又因为BC1⊥B1C，所以BC1⊥平面A1B1CD.‎ 所以A1O为斜线A1B在平面A1B1CD内的射影，∠BA1O为直线A1B与平面A1B1CD所成的角.‎ 在Rt△A1BO中,A1B=,BO=,所以BO=,∠BA1O=30°.‎ 因此,直线A1B和平面A1B1CD所成的角为30°.‎ 变式训练 ‎ 如图10，四面体A—BCD的棱长都相等，Q是AD的中点，求CQ与平面DBC所成的角的正弦值.‎ 图10‎ 解：过A作AO⊥面BCD，连接OD、OB、OC，则可证O是△BCD的中心,‎ 作QP⊥OD,‎ ‎∵QP∥AO,∴QP⊥面BCD.‎ 连接CP，则∠QCP即为所求的角.‎ 设四面体的棱长为a，‎ ‎∵在正△ACD中，Q是AD的中点,∴CQ=.‎ ‎∵QP∥AO，Q是AD的中点,‎ ‎∴QP=，得 sin∠QCP=.‎ 点评：求直线与平面所成的角，是本节的又一重点，作线面角的关键是找出平面的垂线.‎ 思路2‎ 例1 （2007山东高考,文20）如图11(1)，在直四棱柱ABCD—A1B1C1D1中，已知DC=DD1=2AD=2AB，AD⊥DC，AB∥DC.‎ ‎(1)‎ ‎(1)求证：D1C⊥AC1；‎ ‎（2）设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由.‎ ‎（1）证明：在直四棱柱ABCD—A1B1C1D1中，‎ 连接C1D，如图11(2).‎ ‎(2)‎ ‎∵DC=DD1，‎ ‎∴四边形DCC1D1是正方形.‎ ‎∴DC1⊥D1C.‎ 又AD⊥DC，AD⊥DD1，DC∩DD1=D,‎ ‎∴AD⊥平面DCC1D1，D1C平面DCC1D1.‎ ‎∴AD⊥D1C.‎ ‎∵AD、DC1平面ADC1，且AD∩DC1=D,‎ ‎∴D1C⊥平面ADC1.‎ 又AC1平面ADC1，∴D1C⊥AC1.‎ ‎(2)解：连接AD1、AE，如图11(3).‎ ‎(3)‎ 图11‎ 设AD1∩A1D=M,‎ BD∩AE=N,连接MN，‎ ‎∵平面AD1E∩平面A1BD=MN，‎ 要使D1E∥平面A1BD，‎ 需使MN∥D1E，‎ 又M是AD1的中点，‎ ‎∴N是AE的中点.‎ 又易知△ABN≌△EDN，‎ ‎∴AB=DE,‎ 即E是DC的中点.‎ 综上所述，当E是DC的中点时，可使D1E∥平面A1BD.‎ 变式训练 ‎ 如图12，在正方体ABCD—A1B1C1D1，G为CC1的中点，O为底面ABCD的中心.‎ 求证：A1O⊥平面GBD.‎ 图12‎ 证明：BD⊥A1O.‎ 又∵A1O2=A1A2+AO2=a2+()2=,OG2=OC2+CG2=()2+()2=,‎ A1G2=A1C12+C1G2=(a)2+()2=,‎ ‎∴A1O2+OG2=A1G2.‎ ‎∴A1O⊥OG.又BD∩OG=O,∴A1O⊥平面GBD.‎ 点评：判断线面垂直往往转化为线线垂直，勾股定理也是证明线线垂直的重要方法.‎ 例2 如图13，ABCD为正方形，过A作线段SA⊥面ABCD，又过A作与SC垂直的平面交SB、SC、SD于E、K、H，求证：E、H分别是点A在直线SB和SD上的射影.‎ 图13‎ 证明：∵SA⊥BC,‎ 又∵AB⊥BC,SA∩AB=A,‎ ‎∴BC⊥平面SAB.∴BC⊥AE.‎ ‎∵SC⊥平面AHKE,∴SC⊥AE.‎ 又BC∩SC=C,∴AE⊥平面SBC.‎ ‎∴AE⊥SB,即E为A在SB上的射影.同理可证,H是点A在SD上的射影.‎ 变式训练 ‎ 已知Rt△ABC的斜边BC在平面α内，两直角边AB、AC与α都斜交，点A在平面α内的射影是点A′，求证：∠BA′C是钝角.‎ 证明：如图14，过A作AD⊥BC于D，连接A′D，‎ 图14‎ ‎∵AA′⊥α，BCα，∴AA′⊥BC.‎ ‎∴BC⊥A′D.‎ ‎∵tan∠BAD=＜tan∠BA′D=，tan∠CAD=＜tan∠CA′D=，‎ ‎∴∠BAD＜∠BA′D，∠CAD＜∠CA′D.‎ ‎∴∠BAC＜∠BA′C，即∠BA′C是钝角.‎ 知能训练 ‎ 如图15，已知a、b是两条相互垂直的异面直线，线段AB与两异面直线a、b垂直且相交，线段AB的长为定值m，定长为n（n＞m）的线段PQ的两个端点分别在a、b上移动，M、N分别是AB、PQ的中点.‎ 图15‎ 求证：（1）AB⊥MN；‎ ‎（2）MN的长是定值.‎ 证明：(1)取PB中点H,连接HN,则HN∥b.‎ 又∵AB⊥b,∴AB⊥HN.‎ 同理,AB⊥MH.‎ ‎∴AB⊥平面MNH.∴AB⊥MN.‎ ‎(2)∵b⊥平面PAB.∴b⊥PB.‎ 在Rt△PBQ中,BQ2=PQ2-PB2=n2-PB2, ①‎ 在Rt△PBA中,PA2=PB2-AB2=PB2-m2, ②‎ ‎①②两式相加PA2+BQ2=n2-m2,∵a⊥b,∴∠MHN=90°.‎ ‎∴MN=(定值).‎ 拓展提升 ‎1.如图16，已知在侧棱垂直于底面三棱柱ABC—A1B1C1中,AC=3，AB=5，BC=4,AA1=4,点D是AB的中点.‎ 图16‎ ‎（1）求证：AC⊥BC1;‎ ‎（2）求证：AC1∥平面CDB1；‎ ‎（1）证明：∵在△ABC中,AC=3,AB=5,BC=4,‎ ‎∴△ABC为直角三角形.∴AC⊥CB.‎ 又∵CC1⊥面ABC,AC面ABC,∴AC⊥CC1.‎ ‎∴AC⊥面BCC1B1.又BC1面BCC1B1,∴AC⊥BC1.‎ ‎（2）证明：连接B1C交BC1于E，则E为BC1的中点，连接DE,则在△ABC1中,DE∥AC1.‎ 又DE面CDB1,则AC1∥面B1CD.‎ 课堂小结 知识总结：利用面面垂直的性质定理找出平面的垂线，然后解决证明垂直问题、平行问题、求角问题、求距离问题等.‎ 思想方法总结：转化思想，即把面面关系转化为线面关系，把空间问题转化为平面问题.‎ 作业 ‎ 课本习题2.2 B组3、4.‎ 设计感想 ‎ 线面关系是线线关系和面面关系的桥梁和纽带，尤其是线面垂直问题是立体几何的核心，一个立体几何问题能否解决往往取决于能否作出平面的垂线；面面垂直的性质定理恰好能解决这个问题，因此它是高考考查的重点，本节不仅选用了大量经典好题，还选用了大量的2007高考模拟题以及2007年高考题，相信能够帮助大家解决立体几何中的重点难点问题.‎