高中数学常见题型解法归纳及反馈检测 第1讲 函数的定义域常见求法 5页

高中数学常见题型解法归纳及反馈检测 第1讲 函数的定义域常见求法 ‎【知识要点】‎ 一、函数的定义域的定义 函数的定义域是指使函数有意义的自变量的取值范围.‎ 二、求函数的定义域的主要依据 ‎1、分式的分母不能为零.‎ ‎2、偶次方根的被开方数的被开方数必须大于等于零，即中奇次方根的被开方数取全体实数，即中，.‎ ‎3、指数函数的底数必须满足.‎ ‎ 4、对数函数的真数必须大于零，底数必须满足.‎ ‎5、零次幂的底数不能为零，即中.‎ ‎6、正切函数的定义域是.‎ ‎7、复合函数的定义域的求法 ‎（1）已知原函数的定义域为，求复合函数的定义域：只需解不等式，不等式的解集即为所求函数的定义域.‎ ‎（2）已知复合函数的定义域为，求原函数的定义域：只需根据求出函数的值域，即得原函数的定义域.‎ ‎8、求函数的定义域 一般先分别求函数和函数的定义域和，再求，则就是所求函数的定义域.‎ ‎9、求实际问题中函数的定义域 不仅要考虑解析式有意义，还要保证满足实际意义.‎ 第 5 页 高中数学常见题型解法归纳及反馈检测 三、函数的定义域的表示 函数的定义域必须用集合表示，不能用不等式表示.函数的定义域也可以用区间表示，因为区间实际上是集合的一种特殊表示形式.‎ 四、求函数的定义域常用的方法有直接法、求交法、抽象复合法和实际法.‎ 五、函数的问题，必须遵循“定义域优先”的原则.‎ 研究函数的问题，不管是具体的函数，还是抽象的函数，不管是简单的函数，还是复杂的函数，必须优先考虑函数的定义域.之所以要做到这一点，不仅是为了防止出现错误，有时还会为解题带来方便.‎ ‎【方法讲评】‎ 方法1 直接法 使用情景 函数的结构比较简单.‎ 解题步骤 直接列出不等式解答，不等式的解集就是函数的定义域.‎ ‎【例1】求函数的定义域.‎ ‎【反馈检测1】求函数的定义域.‎ 第 5 页 高中数学常见题型解法归纳及反馈检测 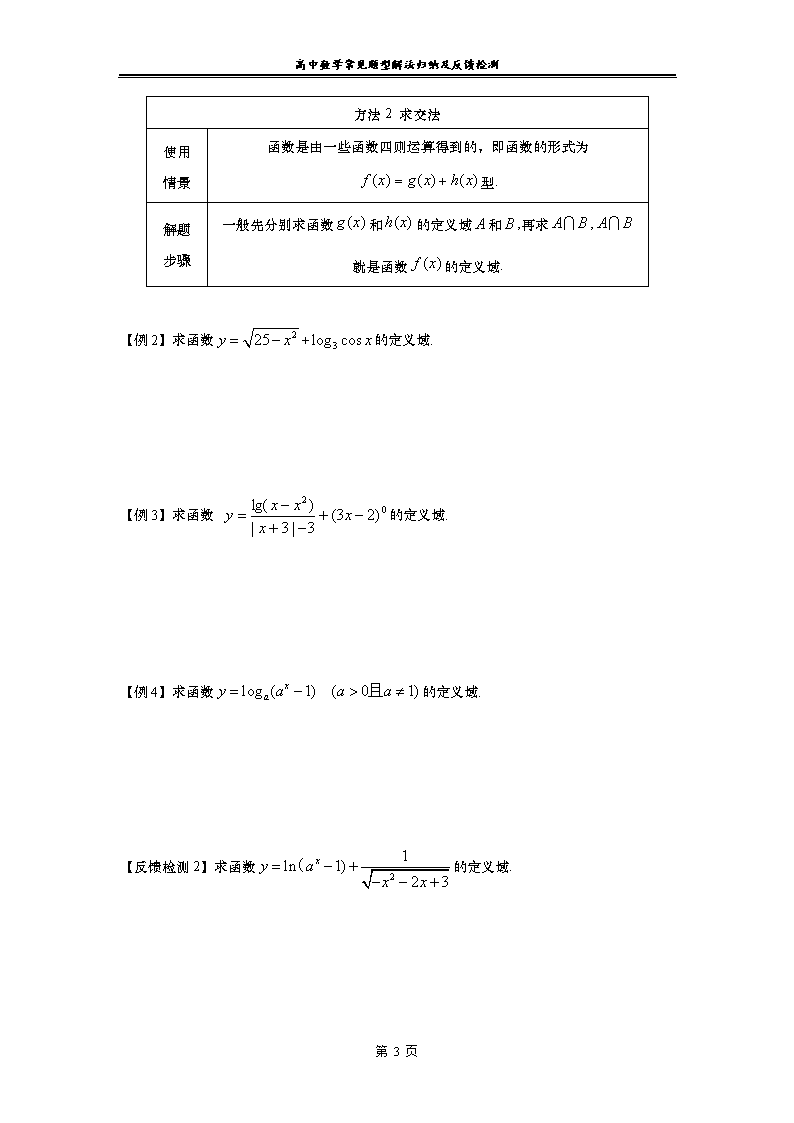方法2 求交法 使用 情景 函数是由一些函数四则运算得到的，即函数的形式为型.‎ 解题 步骤 一般先分别求函数和的定义域和,再求,就是函数的定义域.‎ ‎【例2】求函数+的定义域.‎ ‎【例3】求函数 的定义域.‎ ‎【例4】求函数的定义域.‎ ‎【反馈检测2】求函数的定义域.‎ 第 5 页 高中数学常见题型解法归纳及反馈检测 方法3 抽象复合法 使用 情景 涉及到抽象复合函数.‎ 解题 步骤 利用抽象复合函数的性质解答：‎ ‎（1）已知原函数的定义域为，求复合函数的定义域：只需解不等式，不等式的解集即为所求函数的定义域.‎ ‎（2）已知复合函数的定义域为，求原函数的定义域：只需根据求出函数的值域，即得原函数的定义域.‎ ‎ ‎ ‎【例5】求下列函数的定义域：‎ ‎（1）已知函数的定义域为，求函数的定义域；‎ ‎（2）已知函数的定义域为，求函数的定义域；‎ ‎（3）已知函数的定义域为，求函数的定义域.‎ ‎【反馈检测3】已知函数的定义域为，求函数的定义域.‎ ‎ ‎ ‎【反馈检测4】 若函数的定义域为，求函数的定义域.‎ 第 5 页 高中数学常见题型解法归纳及反馈检测 方法4 实际法 使用 情景 数学问题是实际问题.‎ 解题 步骤 先求函数的自变量的取值范围，再考虑自变量的实际限制条件，最后把前面两者的范围求交集，即得函数的定义域.‎ ‎【例6】用长为的铁丝编成下部为矩形，上部为半圆形的框架（如图所示）.若矩形底边长为，求此框架围成的面积与关于的函数解析式，并求出它的定义域.‎ ‎【反馈检测5】 一个圆柱形容器的底部直径是,高是.现在以的速度向容器内注入某种溶液.求容器内溶液的高度关于注入溶液的时间的函数解析式，并写出函数的定义域和值域.‎ 第 5 页