【新教材】2020-2021学年高中人教A版数学必修第二册课件：8-3-2　圆柱、圆锥、圆台、球的表面积和体积 31页

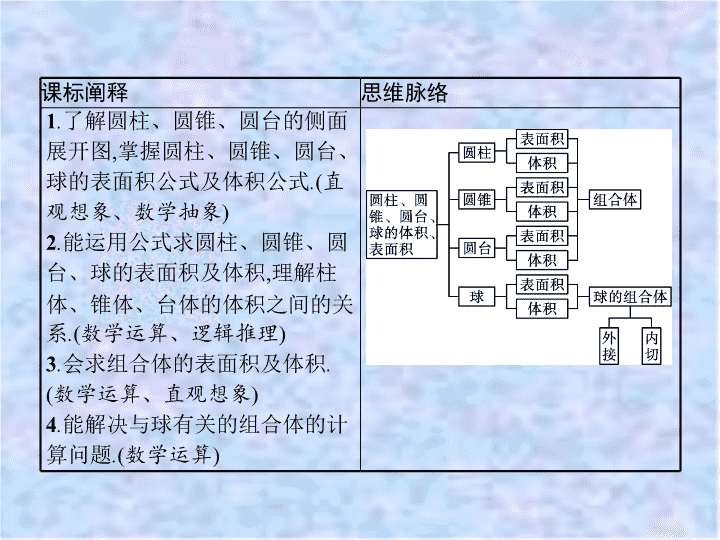
8 . 3 . 2 　 圆柱、圆锥、圆台、球的表面积和体积 课标阐释 思维脉络 1 . 了解圆柱、圆锥、圆台的侧面展开图 , 掌握圆柱、圆锥、圆台、球的表面积公式及体积公式 . ( 直观想象、数学抽象 ) 2 . 能运用公式求圆柱、圆锥、圆台、球的表面积及体积 , 理解柱体、锥体、台体的体积之间的关系 . ( 数学运算、逻辑推理 ) 3 . 会求组合体的表面积及体积 . ( 数学运算、直观想象 ) 4 . 能解决与球有关的组合体的计算问题 . ( 数学运算 ) 激趣诱思 知识点拨 祖暅原理 祖暅是祖冲之的儿子 , 是一位博学多才的数学家 . 唐代王孝通称他为祖暅 , 阮元《畴人传》中称他为祖暅之 , 另字景铄 . 他继承家学 , 主要工作是修补编辑他父亲的著述《缀述》 , 虽然他曾历官员外郎、散骑常侍 . 祖暅在数学上的主要成就 , 就是推算球的体积公式 . 在方法上根据他父亲提出的原理 :“ 缘幂势既同 , 则积不容异 ” . 其中幂指截面积 , 势指高 , 这一原理也可叙述为 :“ 两个等高的立体 , 若平行于底的截面积相等 , 则体积相等 ” . 这个原理 , 西方叫卡瓦列里原理 , 由卡氏于公元 1635 年在《连续不可分量几何》里提出 , 但这比祖冲之父子晚 1 100 多年 . 因而我们将此原理称为 “ 祖氏原理 ” 或 “ 祖暅原理 ” 更为恰当 . 激趣诱思 知识点拨 知识点一、圆柱、圆锥、圆台的 表面积 激趣诱思 知识点拨 微思考 圆柱、圆锥、圆台三者的表面积公式之间有什么关系 ? 提示 : 如图所示 . 激趣诱思 知识点拨 微练习 (1) 圆柱 OO' 的底面直径为 4, 母线长为 6, 则该圆柱的侧面积为 　　　　　 , 表面积为 　　　　　 .  (2) 如图 , 圆锥的底面半径为 1, 高为 , 则圆锥的侧面积为 　 .  (3) 圆台的上、下底面半径分别是 3 和 4, 母线长为 6, 则其表面积等于 　　　　　 .  答案 : (1)24 π 　 32 π 　 (2)2 π 　 (3)67 π 激趣诱思 知识点拨 知识点二、圆柱、圆锥、圆台的体积 1 .V 圆柱 = π r 2 h ( r 是底面半径 , h 是高 ) 名师 点析 棱柱和圆柱都是柱体 , 棱锥和圆锥都是锥体 , 棱台和圆台都是台体 , 它们的体积公式可统一如下 : (1) V 柱体 =Sh ( S 为底面积 , h 为柱体高 ); 激趣诱思 知识点拨 微思考 柱体、锥体、台体的体积公式之间有什么关系 ? 提示 : 如图 . 激趣诱思 知识点拨 微练习 右图是由圆柱与圆锥组合而成的几何体 , 下部是圆柱 , 其轴截面是边长为 4 的正方形 ; 上部为圆锥 , 其高为 3, 则该几何体的体积为 　　　　　 .  解析 : 圆柱的底面半径是 2, 高为 4, 圆锥底面半径是 2, 高为 3, 则 V= π × 2 2 × 4 + × π × 2 2 × 3 = 20 π . 答案 : 20 π 激趣诱思 知识点拨 知识点三、球的表面积和体积 1 .S 球 = 4 π R 2 ( R 是球的半径 ) 2 .V 球 = π R 3 ( R 是球的半径 ) 微练习 已知球的表面积是 16 π , 则该球的体积为 　　　　　 .  解析 : 设球的半径为 R , 则由题意可知 4 π R 2 = 16 π , 解得 R= 2 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 圆柱、圆锥、圆台的表面积 例 1 如图 , 已知直角梯形 ABCD , BC ∥ AD , ∠ ABC= 90°, AB= 5, BC= 16 , AD= 4 . 求 以 AB 所在直线为轴旋转一周所得几何体的表面积 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 解决圆柱、圆锥、圆台的表面积问题 , 要利用好旋转体的轴截面及侧面展开图 , 借助于平面几何知识 , 求得所需几何要素 , 代入公式求解即可 , 基本步骤如下 : (1) 得到空间几何体的平面展开图 ; (2) 依次求出各个平面图形的面积 ; (3) 将各平面图形的面积相加 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 延伸探究 在上题题设条件不变的情况下 , 求以 BC 所在直线为轴旋转一周所得几何体的表面积 . 解 : 以 BC 所在直线为轴旋转一周所得几何体是圆柱和圆锥的组合体 , 如图 . 其中圆锥的高为 16 - 4 = 12, 圆柱的母线长为 AD= 4, 故该几何体的表面积为 2 π × 5 × 4 + π × 5 2 + π × 5 × 13 = 130 π . 探究一 探究二 探究三 探究四 素养形成 当堂检测 圆柱、圆锥、圆台的体积 例 2 已知等边三角形的边长为 2, 将该三角形绕其任一边所在的直线旋转一周而形成的曲面所围成的几何体的体积为 　　　　　 .  分析 将边长为 2 的正三角形绕其任一边所在的直线旋转一周而形成的曲面所围成的几何体是由两个底面半径 为 , 高为 1 的圆锥组成的组合体 , 利用圆锥的体积公式可得结果 . 解析 : 将边长为 2 的正三角形绕其任一边所在的直线旋转一周而形成的曲面所围成的几何体为一个组合体 , 如图 , 该组合体由两个同底的圆锥组成 , 两个圆锥的底面半径 为 , 高为 1, 体积 为 答案 : 2 π 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 求圆柱、圆锥、圆台的体积问题 , 一是要牢记公式 , 然后观察空间图形的构成 , 是单一的旋转体 , 还是组合体 ; 二是注意旋转体的构成 , 以及圆柱、圆锥、圆台轴截面的性质 , 从而找出公式中需要的各个量 , 代入公式计算 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 变式训练 1 用半径为 4 的半圆形铁皮卷成一个圆锥的侧面 , 则此圆锥的体积为 　　　　　 .  探究一 探究二 探究三 探究四 素养形成 当堂检测 球的表面积和体积 例 3 △ ABC 的三个顶点在球 O 的表面上 , 且 AB= 4 , AC= 2, BC= 6 . 球心 O 与 BC 中点的连线长为 4 . 求球的表面积与体积 . 分析 由三边长知 △ ABC 是直角三角形 , 斜边中点为 △ ABC 外接圆圆心 , 则可求球的半径 , 从而求出球的表面积与体积 . 解 : 因为 AB= 4 , AC= 2, BC= 6 , 所以 AB 2 +AC 2 =BC 2 , 即 △ ABC 为直角三角形 . 所以平面 ABC 截球所得截面是以 BC 为直径的圆 . 由已知球心 O 与截面圆心的距离为 4 , 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 因为球的表面积与体积都是球半径的函数 , 所以在解答这类问题时 , 设法求出球的半径是解题的关键 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 变式训练 2 若两球的表面积之差为 48 π , 它们的半径之和为 6, 则两球的体积之差的绝对值为 　　　　　 .  探究一 探究二 探究三 探究四 素养形成 当堂检测 与球有关的组合体 例 4 各棱长均 为 的 四面体内有一内切球 , 求该球的体积 . 分析 等体积法 → 内切球的半径 → 球的体积 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 与球有关的组合体一般有两类 , 一类是与球内接的组合体 , 在此类组合体中 , 球心与多面体顶点的连线是半径 ; 另一类是与球外切的组合体 , 在这一类组合体中 , 球心与各切点的连线是半径 . 在解答与球有关的组合体问题时 , 要注意这些半径的应用 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 延伸探究 求本例所给四面体外接球的表面积 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 转化与化归思想在球的接、切问题中的应用 典例 在半球内有一个内接正方体 , 试求这个半球的体积与正方体的体积之比 . 分析 过正方体的对角面作一截面 , 在这个截面中用正方体的棱长、球半径的关系求解 ; 或将球补为一个整球 , 利用球内接长方体求解 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 ( 方法二 ) 将半球补成整个的球 , 同时把原半球的内接正方体再补接一个同样的正方体 , 构成的长方体刚好是这个球的内接长方体 , 则这个长方体的对角线便是它的外接球的直径 . 设原正方体棱长为 a , 球的半径为 R , 则根据长方体的对角线性质 , 得 方法点睛 球的轴截面 ( 过球心的截面 ) 是将球的问题 ( 立体几何问题 ) 转化为平面问题 ( 圆的问题 ) 的关键 , 因此在解决球的有关问题时 , 我们必须抓住球的轴截面 , 并充分利用它来分析解决问题 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 1 . 直径为 6 的球的表面积和体积分别是 ( 　　 ) A . 36 π ,144 π B . 36 π ,36 π C . 144 π ,36 π D . 144 π ,144 π 解析 : 球的半径为 3, 表面积 S= 4 π ·3 2 = 36 π , 体积 V= π ·3 3 = 36 π . 答案 : B 探究一 探究二 探究三 探究四 素养形成 当堂检测 2 . (2020 北京海淀检测 ) 已知圆锥的顶点为 S , 母线 SA , SB 互相垂直 , SA 与圆锥底面所成角为 30° . 若 △ SAB 的面积为 8, 则该圆锥的体积为 ( 　　 ) A.8 π B . 16 π C . 24 π D . 32 π 答案 : A 探究一 探究二 探究三 探究四 素养形成 当堂检测 3 . 圆台上底面半径为 2, 下底面半径为 6, 母线长为 5, 则圆台的体积为 ( 　　 ) A.40 π B.52 π 解析 : 作出圆台的轴截面如图所示 : 上底面半径 MD= 2, 下底面半径 NC= 6, 过 D 做 DE 垂直 NC , 垂足为 E , 则 EC= 6 - 2 = 4, CD= 5, 故 DE= 3 . 即圆台的高为 3, 所以圆台的体积 为 答案 : B 探究一 探究二 探究三 探究四 素养形成 当堂检测 4 . (2018 全国 Ⅰ 卷 , 文 5) 已知圆柱的上、下底面的中心分别为 O 1 , O 2 , 过直线 O 1 O 2 的平面截该圆柱所得的截面是面积为 8 的正方形 , 则该圆柱的表面积为 ( 　　 ) 解析 : 过直线 O 1 O 2 的平面截该圆柱所得的截面为圆柱的轴截面 , 设底面半径为 r , 母线长为 l , 因为轴截面是面积为 8 的正方形 , 所以 答案 : B 探究一 探究二 探究三 探究四 素养形成 当堂检测 5 . 把 3 个半径为 R 的铁球熔成一个底面半径为 R 的圆柱 , 则圆柱的高为 　　　　　 .  解析 : 设圆柱的高为 h , 则 3 × R 3 = π R 2 · h , 解得 h= 4 R. 答案 : 4 R 6 . 一个正方体的外接球、正方体、正方体的内切球的表面积之比为 　　　　　　　 .  答案 : 3 π ∶ 6 ∶ π