2020届二轮复习不等式学案（全国通用） 13页

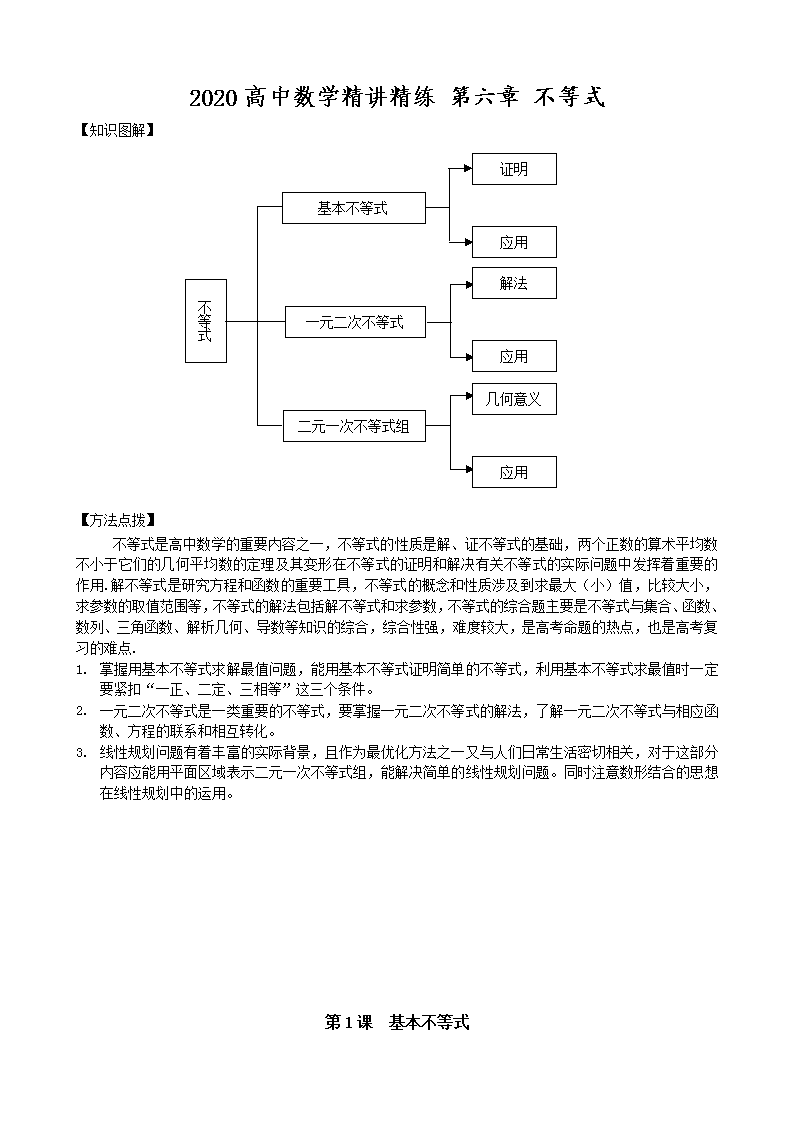
2020 高中数学精讲精练 第六章 不等式 【知识图解】 【方法点拨】 不等式是高中数学的重要内容之一，不等式的性质是解、证不等式的基础，两个正数的算术平均数 不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的 作用.解不等式是研究方程和函数的重要工具，不等式的概念和性质涉及到求最大（小）值，比较大小， 求参数的取值范围等，不等式的解法包括解不等式和求参数，不等式的综合题主要是不等式与集合、函数、 数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复 习的难点. 1. 掌握用基本不等式求解最值问题，能用基本不等式证明简单的不等式，利用基本不等式求最值时一定 要紧扣“一正、二定、三相等”这三个条件。 2. 一元二次不等式是一类重要的不等式，要掌握一元二次不等式的解法，了解一元二次不等式与相应函 数、方程的联系和相互转化。 3. 线性规划问题有着丰富的实际背景，且作为最优化方法之一又与人们日常生活密切相关，对于这部分 内容应能用平面区域表示二元一次不等式组，能解决简单的线性规划问题。同时注意数形结合的思想 在线性规划中的运用。 第 1 课　基本不等式 不 等 式 一元二次不等式 基本不等式 二元一次不等式组 应用 解法 应用 几何意义 应用 证明 【考点导读】 1. 能用基本不等式证明其他的不等式，能用基本不等式求解简单的最值问题。 2. 能用基本不等式解决综合形较强的问题。 【基础练习】 1.“a>b>0”是“ab< ”的充分而不必要条件(填写充分而不必要条件、必要而不充分条件、充分必 要条件、既不充分也不必要条件) 2. 的最小值为 3.已知 ，且 ，则 的最大值为 4.已知 ，则 的最小值是 2 【范例导析】 例 1.已知 ，求函数 的最大值. 分析：由于 ，所以首先要调整符号. 解：∵ ∴ ∴y=4x-2+ = ≤-2+3=1 当且仅当 ，即 x=1 时，上式成立，故当 x=1 时， . 例 2.（1）已知 a，b 为正常数，x、y 为正实数，且 ，求 x+y 的最小值。 （2） 已知 ，且 ，求 的最大值． 分析：问题（1）可以采用常数代换的方法也可以进行变量代换从而转化为一元函数再利用基本不等式求 解；问题（2）既可以直接利用基本不等式将题目中的等式转化为关于 的不等式，也可以采用变量代换 转换为一元函数再求解. 解:(1)法一：直接利用基本不等式： ≥ 当且仅当 ，即 时等号成立 法二： 2 2 2 a b+ cabcabaccbba ++=+=+=+ 则,2,2,1 222222 1 32 − ,x y R+∈ 4 1x y+ = x y⋅ 16 1 lg lg 1x y+ = 5 2 x y + 5 4x < 14 2 4 5y x x = − + − 4 5 0x − < 5 4x < 5 4 0x− > 1 4 5x − 15 4 35 4x x  − − + + −  15 4 5 4x x − = − max 1y = 1a b+ =x y 00 >> yx ， 302 =++ xyyx xy xy a b bx ayx+ y = (x+ y)( + )= a+b+ +x y y x a+b+ 2 ab ay bx=x y a b+ = 1x y     x = a+ ab y = b+ ab   由 得 ∵ x>0，y>0，a>0 ∴ 由 >0 得 y-b>0 ∴ x+y≥ 当且仅当 ，即 时，等号成立 （2）法一：由 ，可得， ． 注意到 ．可得， ． 当且仅当 ，即 时等号成立，代入 中得 ，故 的最大值为 18． 法二： ， ， 代入 中得： 解此不等式得 ．下面解法见解法一，下略． 点拨：求条件最值的问题，基本思想是借助条件化二元函数为一元函数，代入法是最基本的方法，也可考 虑通过变形直接利用基本不等式解决. 【反馈练习】 1.设 a＞1,且 ,则 的大小关系为 m＞p＞n 2.已知下列四个结论： ①若 则 ； ②若 ,则 ； ③若 则 ； ④若 则 。 其中正确的是④ a b+ = 1x y ayx = y - b ay a( y b ) abx y y yy b y b ab aba y ( y b ) a by b y b − ++ = + = +− − = + + = + − + +− − ∴ ay y - b 2 ab + a+b ab = y - by - b a b+ = 1x y     y = b+ ab x = a+ ab   302 =++ xyyx )300(2 30 <<+ −= xx xy x xx x xxxy + −+++−=+ −= 2 64)2(34)2( 2 30 22     +++−= 2 64)2(34 xx 162 64)2(22 64)2( =+⋅+≥+++ xxxx 18≤xy 2 642 +=+ xx 6=x 302 =++ xyyx 3=y xy +∈ Ryx, xyxyyx ⋅=≥+∴ 22222 302 =++ xyyx 3022 ≤+⋅ xyxy 180 ≤≤ xy 2log ( 1), log ( 1), log (2 )a a am a n a p a= + = − = pnm ,, ,, Rba ∈ 22 =⋅≥+ b a a b b a a b +∈ Ryx, yxyx lglg2lglg ≥+ ,−∈ Rx 4424 −=⋅−≥+ xxxx ,−∈ Rx 222222 =⋅≥+ −− xxxx 3.已知不等式 对任意正实数 恒成立，则正实数 的最小值为 6 4.（1）已知： ，且： ，求证： ，并且求等号成立的条件． （2）设实数 x，y 满足 y+x2=0，0 >x y 1=xy 22 22 ≥− + yx yx ( )x y alog a +a 1log 2 8 +a +∈ Ryx， yx − xyyx 2≥+ )( 1)( yxyx −+− ,1.0,0 =>−∴>> xyyxyx  又 yx xyyx yx yx − +−=− +∴ 2)( 222 yxyx −+−= 2)( .22)( 2)(2 =−⋅−≥ yxyx )( 2)( yxyx −=− .4,2,2)( 222 =+=−=−∴ yxyxyx ,6)(,1 2 =+∴= yxxy .6=+∴ yx 2 26,2 26 −=+= yx 2 26,2 26 −=+= yx yx aa + 8 1) 2 1x( 2 1 2 xx yx 2 2 a2a2a2 +−−− + == 8 1)2 1x(2 1 2 +−− 8 1 8 1) 2 1x( 2 1 2 a2 +−− 8 1 a2 yx aa + 8 1 a2 )aa(log yx a + 8 12log)a2(log a 8 1 a += 第 2 课　一元二次不等式 【考点导读】 1. 会解一元二次不等式，了解一元二次不等式与相应函数、方程之间的联系和转化。 2. 能运用一元二次不等式解决综合性较强的问题. 【基础练习】 1.解不等式： （1） （2） （3） （4） 解：（1）原不等式化为 ，解集为 （2）原不等式化为 ，解集为 R （3）原不等式化为 ，解集为 （4）由 得 点拨：解一元二次不等式要注意二次项系数的符号、对应方程 的判断、以及对应方程两根大小的比较. 2. 函数 的定义域为 3..二次函数 y=ax2+bx+c(x∈R)的部分对应值如下表： 则不等式 ax2+bx+c>0 的解集是 4.若不等式 的解集是 ，则 b=__-2____ c=__-3____. 【范例导析】 例.解关于ｘ的不等式 分析：本题可以转化为含参的一元二次不等式，要注意分类讨论. 解:原不等式等价于 ∵ ∴等价于： 23 4 4 0x x− + + > 21 3 02 2x x+ + > ( )( ) 21 3 2 2x x x x+ − > − − 22 3 2 14 2 −<−−−<− xx 23 4 4 0x x− − < 2 23 x− < < 2 2 3 0x x+ + > 2 1 0x x+ + < ∅ 2 2 2 2 2 1 3 4 2 1 01 3 2 22 4, ,1 32 2 2 5 022 2 x x x xx x x xx x  + + <  + − > < + + <   + − < + + > 得 得 2 1 2 1, 6 1 6 1 x x x  > − < − − − − < < − 或 ( 6 1, 2 1) ( 2 1, 6 1)x∴ ∈ − − − − − − ∆ )1(log 2 2 1 −= xy ) (2, 1 1, 2 − −  ),3()2,( +∞−−∞  02 >++ cbxx }13{ −<> xxx 或 )1(12 )1( ≠>− − ax xa 02 )2()1( >− −−− x axa 1≠a x -3 -2 -1 0 1 2 3 4 y 6 0 -4 -6 -6 -4 0 6 （*） a>１时，（*）式等价于 >0∵ <１∴x< 或 x>２ a<１时，（*）式等价于 <0 由２－ ＝ 知： 当 0２，∴２１时，原不等式的解集为（－∞， ）∪（2，＋∞）。 思维点拨:含参数不等式,应选择恰当的讨论标准对所含字母分类讨论,要做到不重不漏. 【反馈练习】 1.若关于 x 的不等式 的解集为 R，则 的取值范围是 2.不等式 解集为 ，则 ab 值分别为-12，-2 3.若函数 f(x) = 的定义域为 R，则 的取值范围为 4.已知 M 是关于 x 的不等式 2x2+(3a－7)x+3＋a－2a2<0 解集，且 M 中的一个元素是 0，求实数 a 的取值范 围，并用 a 表示出该不等式的解集. 解：原不等式即(2x－a－1)(x＋2a－3)<0， 由 适合不等式故得 ，所以 ，或 . 若 ，则 ，∴ ， 此时不等式的解集是 ； 若 ，由 ，∴ ， 此时不等式的解集是 。 第 3 课　线性规划 【考点导读】 1. 会在直角坐标系中表示二元一次不等式、二元一次不等式组对应的区域，能由给定的平面区域确定所 ( ) 02 1 21 >−      − −−− x a axa 2 1 2 − − −− x a ax 1 111 2 −−=− − aa a 1 2 − − a a 2 1 2 − − −− x a ax 1 2 − − a a 1−a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 1 2 − − a a 2 1 0,ax ax a+ + − < a ( ],0−∞ 2 2 0ax bx+ + > 1 1 2 3x− < < 2 22 1x ax a− − − a [ ]1 0− ， 0=x 0)32)(1( >−+ aa 1−a 1−+−=+−+− aaa 2 123 +>− aa }232 1|{ axax −<<+ 2 3>a 4 5)1(2 5 2 132 −<+−=+−+− aaa 2 123 +<− aa }2 123|{ +<<− axax 对应的二元一次不等式、二元一次不等式组. 2. 能利用图解法解决简单的线性规划问题，并从中体会线性规划所体现的用几何图形研究代数问题的思 想. 【基础练习】 1.原点（0,0）和点 P（1,1）在直线 的两侧，则 a 的取值范围是 0 ， (0 2)， ( 2 0)− ， (0 2)−， (2 0)， 2 0 2 1 0 2 1 0 x y x y x y + + >  + + <  + + <  +−≤ −≥ 13 1 xy xy 2 3    ≥ ≤+ −≤− 1 2553 34 x yx yx ABC∆ 5 22 例 1 图 当 L0 的平行线过 B 点时，可使 z=6x+10y 达到最小值 当 L0 的平行线过 A 点时，可使 z=6x+10y 达到最大值 所以 zmin=16;zmax=50 点拨：几个结论：(1)、线性目标函数的最大（小）值一般在可行域的顶点处取得，也可能在边界处取得。 （2）、求线性目标函数的最优解，要注意分析线性目标函数所表示的几何意义——在 y 轴上的截距或其相 反数。 例 2.已知 ， （1） 求 的最大和最小值。 （2） 求 的取值范围。 （3） 求 的最大和最小值。 解析：注意目标函数是代表的几何意义. 解：作出可行域。 （1） ，作一组平行线 l： ，解方程组 得最优解 B （3，1）， 。解 得最优解 C（7，9）， （2） 表示可行域内的点（x,y）与（0，0）的连线的斜率。从图中可得， ， 又 ， 。 （3） 表示可行域内的点（x,y）到（0，0）的距离的平方。从图中易 得 ， ，（ OF 为 O 到 直 线 AB 的 距 离 ）， 。 ， ， ， 。 点拨：关键要明确每一目标函数的几何意义，从而将目标函数的最值问题转化为某几何量的取值范围. 例 3．本公司计划 2008 年在甲、乙两个电视台做总时间不超过 300 分钟的广告，广告总费用不超过 9 万元， 甲、乙电视台的广告收费标准分别为 元/分钟和 200 元/分钟，规定甲、乙两个电视台为该公司所做的 每分钟广告，能给公司事来的收益分别为 0.3 万元和 0.2 万元．问该公司如何分配在甲、乙两个电视台的 广告时间，才能使公司的收益最大，最大收益是多少万元？ 分析：本例是线性规划的实际应用题，其解题步骤是：（1）设出变量，列出约束条件及目标函数；（2） 画出可行域（3）观察平行直线系 的运动，求出目标函数的最值. 解：设公司在甲电视台和乙电视台做广告的时间分别为 分钟和 分钟，总收益为 元，由题意得    ≤−− ≥−+ ≥+− 052 04 02 yx yx yx yxz 2+= x yz = 22 yxz += 12 2 2 zz x y y x= + ⇔ = − + 1 2 2 zy x= − + 04 052{ =−+ =−− yx yx 3 2 1 5minz∴ = + × = 02 052{ =+− =−− yx yx max 7 2 9 25z∴ = + × = 0 0 − −== x y x yz k z kOB OA ≤ ≤ 13, 3k kOA OB = = 1 33 z∴ ≤ ≤ 2 2 2 2( 0) ( 0)z x y x y= + = − + − 2 minz OF= 2 maxz OC= 0 0 4 2 2 2 OF + −= = 2 28, 130OF OC= = 130maxz∴ = 8minz = 500 3000 2000z x y= + x y z 目标函数为 ． 二元一次不等式组等价于 作出二元一次不等式组所表示的平面区域，即可行域． 如图： 作直线 ， 即 ． 平移直线 ，从图中可知，当直线 过 点时，目标函数取得最大值． 联立 解得 ． 点 的坐标为 ． （元） 答：该公司在甲电视台做 100 分钟广告，在乙电视台做 200 分钟广告，公司的收益最大，最大收益是 70 万元． 【反馈练习】 1.不等式组 表示的平面区域是一个三角形，则 的取值范围是 2.已知点 P（x，y）在不等式组 表示的平面区域上运动，则 z＝x－y 的取值范围是[－1，2] 3.设 、 满足约束条件 则使得目标函数 的最大的点 是（2,3）． 4.已知实数 满足 则 的取值范围是 5.画出以 A（3，－1）、B（－1，1）、C（1，3）为顶点的△ABC 的区域（包括各边），写出该区域所表示 300 500 200 90000 0 0. x y x y x y +  +  ≤ ， ≤ ， ≥ ， ≥ 3000 2000z x y= + 300 5 2 900 0 0. x y x y x y +  +  ≤ ， ≤ ， ≥ ， ≥ :3000 2000 0l x y+ = 3 2 0x y+ = l l M 300 5 2 900. x y x y + =  + = ， 100 200x y= =， ∴ M (100 200)， max 3000 2000 700000z x y∴ = + = 5 0 2 x y y a x − + 0   ≥ ， ≥ ， ≤ ≤ a 5 7a <≤    ≥−+ ≤− ≤− 022 ,01 ,02 yx y x x y 5, 3 2 12, 0 3, 0 4. x y x y x y + ≤  + ≤ ≤ ≤  ≤ ≤ 6 5z x y= + ( , )x y x y， 2 2 0 3 x y x y y +  −  ≥ ， ≤ ， ≤ ≤ ， 2z x y= − [ ]5 7− ， 0 100 200 300 100 200 300 400 500 y x l M 例 3 的二元一次不等式组，并求以该区域为可行域的目标函数 z=3x－2y 的最大值和最小值. 分析：本例含三个问题：①画指定区域；②写所画区域的代数表达式——不等式组；③求以所写不等式组 为约束条件的给定目标函数的最值 解：如图，连结点 A、B、C，则直线 AB、BC、CA 所围成的区域为所求△ABC 区域 直线 AB 的方程为 x+2y－1=0，BC 及 CA 的直线方程分别为 x－y+2=0，2x+y－5=0 在△ABC 内取一点 P（1，1）， 分别代入 x+2y－1，x－y+2，2x+y－5 得 x+2y－1>0，x－y+2>0，2x+y－5<0 因此所求区域的不等式组为 x+2y－1≥0，x－y+2≥0，2x+y－5≤0 作平行于直线 3x－2y=0 的直线系 3x－2y=t（t 为参数），即平移直线 y= x，观察图形可知：当直线 y= x － t 过 A（3，－1）时，纵截距－ t 最小此时 t 最大，tmax=3×3－2×（－1）=11；当直线 y= x－ t 经过点 B（－1，1）时，纵截距－ t 最大，此时 t 有最小值为 tmin= 3×（－1）－2×1=－5 因此，函数 z=3x－2y 在约束条件 x+2y－1≥0，x－y+2≥0，2x+y－5≤0 下的最大值为 11，最小值为－5 。 第 4 课　不等式综合 【考点导读】 能利用不等式性质、定理、不等式解法及证明解决有关数学问题和实际问题，如最值问题、恒成立问 题、最优化问题等. 【基础练习】 1. 若 函 数 ， 则 与 的 大 小 关 系 是 2 3 2 3 2 1 2 1 2 3 2 1 2 1 ( ) ( ) ( ) ( ) 2 21 12 , 02 2 x f x x x g x xx − = + > = ≠ −   ( )f x ( )g x ( ) ( )f x g x> 第 10 题 2.函数 在区间 上恒为正，则 的取值范围是 0＜a＜2 3.当点 在直线 上移动时， 的最小值是 7 4.对于 0≤m≤4 的 m，不等式 x2+mx＞4x+m－3 恒成立，则 x 的取值范围是 x＞3 或 x＜－1 【范例导析】 例 1、已知集合 ，函数 的定义域为 Q （1）若 ，求实数 a 的取值范围。 （2）若方程 在 内有解，求实数 a 的取值范围。 分析：问题（1）可转化为 在 内有有解；从而和问题（2）是同一类型的问题，既 可以直接构造函数角度分析，亦可以采用分离参数. 解：（1）若 ， 在 内有有解 令 当 时， 所以 a>-4,所以 a 的取值范围是 （2）方程 在 内有解， 则 在 内有解。 当 时， 所以 时， 在 内有解 点拨：本题用的是参数分离的思想. 例 2.甲、乙两地相距 ，汽车从甲地匀速行驶到乙地，速度不超过 ，已知汽车每小时的运输成 本（以元为单位）由可变部分和固定部分组成：可变部分与速度 的平方成正比，且比例系数为 ； 固定部分为 元． （1）把全程运输成本 元表示为速度 的函数，并指出这个函数的定义域； ( ) ( )22f x a x a= − + [ ]0,1 a ( ),x y 3 2 0x y+ − = 3 27 1x yz = + +    = 2,2 1P ( )22log 2 2 +−= xaxy φ≠QP  ( ) 222log 2 2 =+− xax     2,2 1 2 2 2 0ax x− + >     2,2 1 φ≠QP  0222 >+−∴ xax     2,2 1 xxa 22 2 +−>∴ 2 1 2 11222 2 2 +     −−=+−= xxxu    ∈ 2,2 1x    −∈ 2 1,4u { }4−>aa ( ) 222log 2 2 =+− xax     2,2 1 0222 =−− xax     2,2 1 2 1 2 11222 2 2 −     +=+=∴ xxxa    ∈ 2,2 1x    ∈ 12,2 3a    ∈ 12,2 3a ( ) 222log 2 2 =+− xax     2,2 1 kms km/hc km/hv b a y km/hv （2）为了使全程运输成本最小，汽车应以多大速度行驶？ 分析：需由实际问题构造函数模型，转化为函数问题求解 解：（1）依题意知汽车从甲地匀速行驶到乙地所用的时间为 ，全程运输成本为 ．故所求函数为 ，定义域为 ． （2）由于 都为正数， 故有 ，即 ． 当且仅当 ，即 时上式中等号成立． 若 时，则 时，全程运输成本 最小； 当 ，易证 ，函数 单调递减，即 时， ． 综上可知，为使全程运输成本 最小， 在 时，行驶速度应为 ； 在 时，行驶速度应为 ． 点拨：本题主要考查建立函数关系式、不等式性质（公式）的应用．也是综合应用数学知识、思想和 方法解决实际问题的一道优秀试题． 【反馈练习】 1.设 ，函数 ，则使 的 的取值范围是 2.如果函数 的单调递增区间是(-∞，a]，那么实数 a 的取值范围是____ a<-1____ 3.若关于 的不等式 对任意 恒成立，则实数 的取值范围为 4 已知二次函数 f (x)= ,设方程 f (x)=x 的两个实根为 x1 和 x2．如果 x1<2＜x2<4， 且函数 f (x)的对称轴为 x=x0，求证：x0＞—1． 证 明 ： 设 g(x)= f (x)—x= ， 且 g(4)>0 ， 即 hv s )(2 bvv asv sbvv say +=⋅+⋅= )( bvb asy += )0( cv ，∈ vbas 、、、 bvb asbvv as ⋅⋅≥+ 2)( absbvv as 2)( ≥+ bvv a = b av = cb a ≤ b av = y cb a ≤ cv <<0 )()( bvv asvfy +== cv = )(min bcc asy += y cb a ≤ b av = cb a ≤ cv = 10 << a )22(log)( 2 −−= xx a aaxf 0)( ∈++ aRbabxax 且 ( ) ( ) 0242.011 21 2 <<<<>+−+ gxxaxbax 得，由，且 ,8 1,22 144 3,22 144 3 ,03416 ,0124 >−<−−<<−∴    <−+ <−+ aaaababa ba 得由 ∴ .1 8 14 112,4 1128 32 −= ⋅ −>−=−>−>− a bxaa b a 故