- 508.30 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
云浮市2019~2020学年第二学期高二期末检测
数 学
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:人教A版选修2-2,2-3.
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数满足,则( )
A.1 B. C.2 D.4
2.已知函数,则( )
A. B. C.2 D.4
3.( )
A. B. C. D.
4.某演讲比赛候选人中高一学生5名,高二学生4名,高三学生3名,从每个年级中各选1人参加市团委组织的演讲比赛,则不同的选法有( )
A.60种 B.45种 C.30种 D.12种
5.若的展开式中第3项和第5项的二项式系数相等,则展开式中所有二项式系数和为( )
A.16 B.32 C.64 D.128
6.某中学有三栋教学楼,如图所示,若某学生要从处到达他所在的班级处(所有楼道间是连通的),则最短路程不同的走法数为( )
A.5 B.10 C.15 D.21
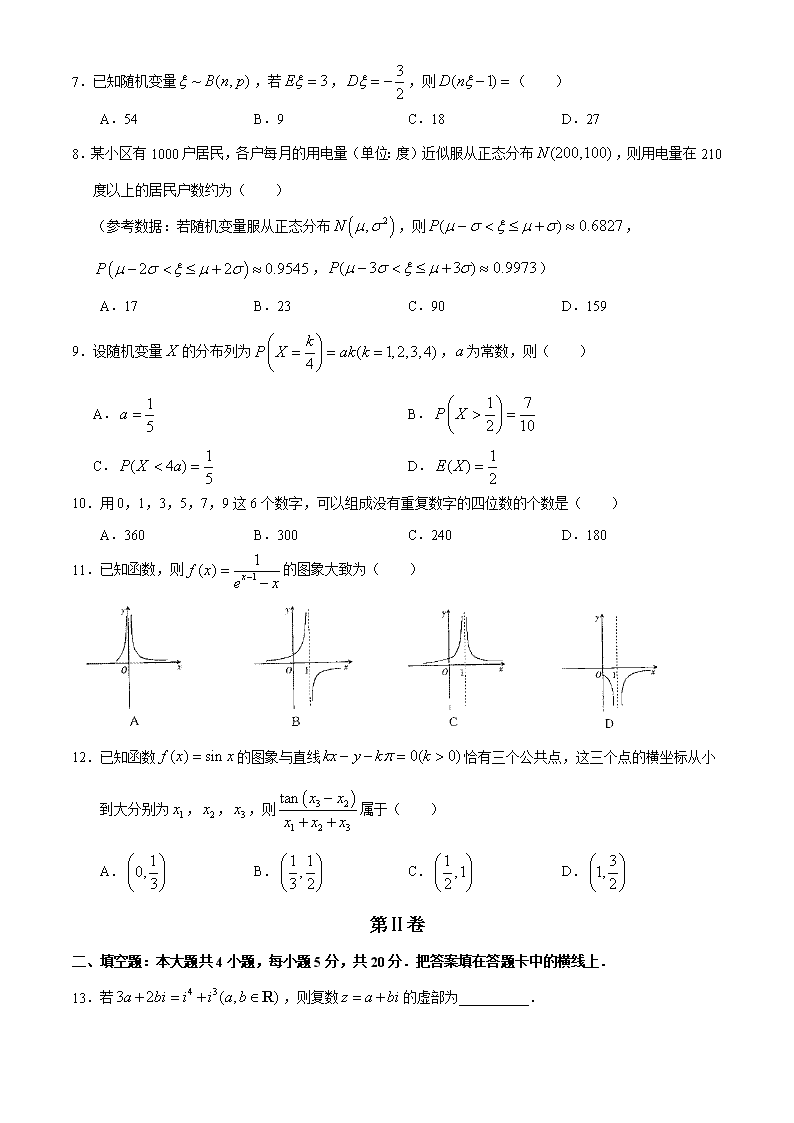
7.已知随机变量,若,,则( )
A.54 B.9 C.18 D.27
8.某小区有1000户居民,各户每月的用电量(单位:度)近似服从正态分布,则用电量在210度以上的居民户数约为( )
(参考数据:若随机变量服从正态分布,则,,)
A.17 B.23 C.90 D.159
9.设随机变量的分布列为,为常数,则( )
A. B.
C. D.
10.用0,1,3,5,7,9这6个数字,可以组成没有重复数字的四位数的个数是( )
A.360 B.300 C.240 D.180
11.已知函数,则的图象大致为( )
12.已知函数的图象与直线恰有三个公共点,这三个点的横坐标从小到大分别为,,,则属于( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.若,则复数的虚部为__________.
14.函数的极大值为__________.
15.根据某地区气象台统计,该地区下雨的概率是,刮风的概率为,既刮风又下雨的概率为,则在刮风天里,下雨的概率为__________,在下雨天里,刮风的概率为__________.(本题第一空2分第二空3分)
16.已知函数的定义域是,关于函数给出下列命题:
①对于任意,函数是上的增函数;
②对于任意,函数存在最小值;
③存在,使得对于任意的,都有成立;
④存在,使得函数有两个零点.
其中正确命题的序号是__________.(写出所有正确命题的序号)
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知函数.
(1)若曲线在点处的切线与直线平行,求的值;
(2)若函数在上是单调递增函数,求的取值范围.
18.(12分)
某大学读书协会为了解本校大学生网上阅读与传统纸质阅读的情况,调查了该大学1000名大学生(男、女各占一半),就偏向网上阅读和偏向传统纸质阅读的情况作了调查记录.记录显示,偏向网上阅读的男大学生比偏向传统纸质阅读的男大学生多300人,这1000名大学生中,偏向传统纸质阅读的大学生共有400人.
(2)根据题意,完成下列2×2列联表:
阅读方式
性别
偏向网上阅读
偏向传统纸质阅读
总计
男
女
总计
1000
(2)根据列联表,判断能否有99.9%的把握认为该大学的大学生的阅读方式与性别有关,说明你的理
由.
附:.
0.050
0.010
0.001
3.841
6.635
10.828
19.(12分)
(1)求的展开式的各项系数之和及展开式的常数项.
(2)4位男同学与3位女同学任意排成一排照相.
(i)求3位女同学站在一起的概率;
(ii)求4位男同学互不相邻的概率.
20.(12分)
某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大.
21.(12分)
为了解某企业生产的某产品的年利润与年广告投入的关系,该企业对最近一些相关数据进行了调查统计,得出相关数据见下表:
年广告投入(万元)
2
3
4
5
6
年利润(十万元)
3
4
6
8
11
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程:方程甲,;方程乙,.
(1)求(结果精确到0.01)与的值.
(2)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(备注:,称为相应于点的残差);
年广告投入(万元)
2
3
4
5
6
年利润(十万元)
3
4
6
8
11
模型甲
估计值
残差
模型乙
估计值
残差
②分别计算模型甲与模型乙的残差平方和及,并通过比较,的大小,判断哪一个模型拟合效果更好.
22.(12分)
已知函数.
(1)当时,证明:;
(2)若函数,证明:函数存在极小值.
云浮市2019~2020学年第二学期高二期末检测
数学参考答案
1.B ,则.
2.A 因为所以.
3.D .
4.A 由乘法计数原理可得共有种不同的选法.
5.C 因为的展开式中第3项和第5项的二项式系数相等,
所以,所以展开式中所有二项式系数和为.
6.D 从到共需走7步,其中横步(向右)有2步,竖直向上的有5步,
故最短路程的不同走法数为.
7.A 因为随机变量,,,
所以,解得,
因此.
8.D 由题得,,
所以,
所以,
所以用电量在210度以上的居民户数为.
9.B 因为,所以,
所以,,.
10.B 当四个数字中没有0时,没有重复数字的四位数有种;
当四个数字中有0时,没有重复数字的四位数有种,两类相加一共有300种.
11.C 令,则,
在上单调递减,在上单调递增,
又,所以当时,,即,故选C.
12.B 函数的图象关于对称,直线过,
作出函数的图象与直线恰有三个公共点的图象,
由图象可知,,且.
由于,,所以,
即,所以.
13. ,则,,
所以,虚部为.
14. 依题意得,
所以当时,;当时,.
所以当时,函数有极大值.
15.,
设“下雨”,“刮风”,“刮风又下雨”,
所以在刮风天里,下雨的概率为,
所以在下雨天里,刮风的概率为.
16.①②④
函数的定义域是,且,
当时,在上恒成立,
所以函数在上单调递增,故①对;
对于,存在,使,
则在上单调递减,在上单调递增,
所以对于任意,函数存在最小值,故②正确;
函数与,的图象在上有公共点,
所以对于任意,有零点,故③错误;
由②得函数存在最小值,且存在,
使,故④正确.
故填①②④.
17.解:(1)由题可知,则,
解得.
(2)∵在上是增函数,
∴对恒成立,所以,
只需,故的取值范围是.
18.解:列联表如下:
阅读方式
性别
偏向网上阅读
偏向传统纸质阅读
总计
男
400
100
500
女
200
300
500
总计
600
400
1000
(2)因为,
所以有99.9%的把握认为该大学的大学生的阅读方式与性别有关.
19.解:(1)令,得的展开式的各项系数之和为,
常数项为.
(2)(i)3位女同学站在一起的概率为.
(ii)4位男同学互不相邻的概率为.
20.解:(1)设甲正确完成面试的题数为,则的取值分别为1,2,3.
,,.
应聘者甲正确完成题数的分布列为
1
2
3
.
设乙正确完成的面试题数为,则的取值可能为0,1,2,3.
;;
;.
应聘者乙正确完成题数的分布列为
0
1
2
3
.
(或因为,所以)
(2)因为,
,所以.
综上所述,从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;从至少完成2道题的概率考查,甲获得面试通过的可能性大.
21.解:(1)设,则,
因为,
所以,解得.
又,所以,解得.
(2)①经计算,可得下表:
年广告投入(万元)
2
3
4
5
6
年利润(十万元)
3
4
6
8
11
模型甲
估计值
3.08
4.07
5.72
8.03
11
残差
0.28
0
模型乙
估计值
2.4
4.4
6.4
8.4
10.4
残差
0.6
0.6
②,
,
因为,所以模型甲的拟合效果更好.
22.解:(1)依题意,,
因为,且,故,
故函数在上单调递减,
故.
(2)依题意,,,
令,则.
而,可知当时,,
故函数在上单调递增,
故当时,.
当时,函数单调递增,而,
又,
故,使得,
故,使得,即函数单调递增,即单调递增,
故当时,,
故函数在上单调递减,在上单调递增,
故当时,函数有极小值.