高考数学复习专题练习第4讲 二元一次不等式（组）与简单的线性 8页

第4讲 二元一次不等式（组）与简单的线性 ‎ 规划问题 一、选择题 ‎1．不等式2x－y≥0表示的平面区域是(　　)‎ 解析 取测试点(1,0)，排除B、D，又边界应为实线，故排除C.‎ 答案 A ‎2．已知平面直角坐标系xOy上的区域D由不等式组给定．若M(x，y)为D上的动点，点A的坐标为(，1)则z＝·的最大值为(　　)．‎ A．4 B．‎3‎ C．4 D．3‎ 解析　如图作出区域D，目标函数z＝x＋y过点B(，2)时取最大值，故z的最大值为×＋2＝4，故选C.‎ 答案　C ‎3．若不等式组 ‎ 表示的平面区域是一个三角形，则a的取值范围是 (　　)．‎ A．(－∞，5) B．[7，＋∞)‎ C．[5,7) D．(－∞，5)∪[7，＋∞)‎ 解析　画出可行域，知当直线y＝a在x－y＋5＝0与y轴的交点(0,5)和x－y＋5＝0与x＝2的交点(2,7)之间移动时平面区域是三角形．故5≤a<7.‎ 答案　C ‎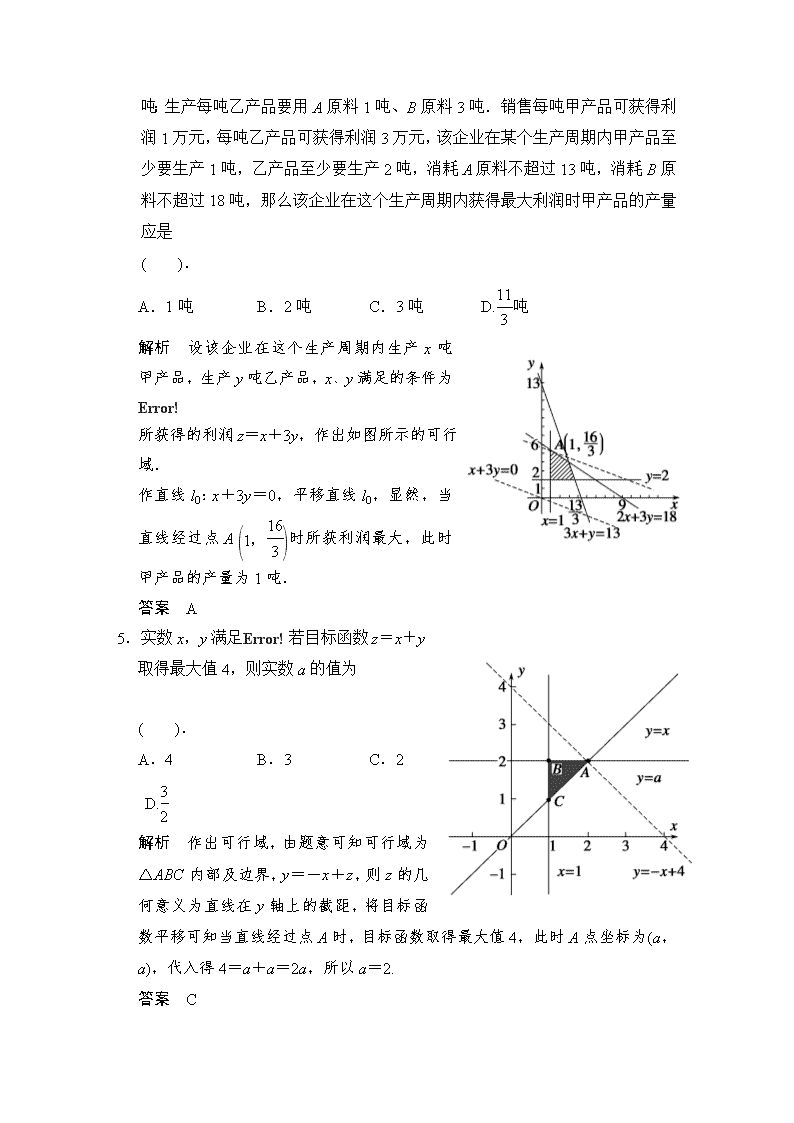4．某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨、B 原料2吨；生产每吨乙产品要用A原料1吨、B原料3吨．销售每吨甲产品可获得利润1万元，每吨乙产品可获得利润3万元，该企业在某个生产周期内甲产品至少要生产1吨，乙产品至少要生产2吨，消耗A原料不超过13吨，消耗B原料不超过18吨，那么该企业在这个生产周期内获得最大利润时甲产品的产量应是 (　　)．‎ A．1吨 B．2吨 C．3吨 D.吨 解析　设该企业在这个生产周期内生产x吨甲产品，生产y吨乙产品，x、y满足的条件为 所获得的利润z＝x＋3y，作出如图所示的可行域．‎ 作直线l0：x＋3y＝0，平移直线l0，显然，当直线经过点A时所获利润最大，此时甲产品的产量为1吨．‎ 答案　A ‎5．实数x，y满足若目标函数z＝x＋y取得最大值4，则实数a的值为 (　　)．　　　　　　　　　　　　　　　　　　　‎ A．4 B．‎3 ‎ C．2 D. 解析　作出可行域，由题意可知可行域为△ABC内部及边界，y＝－x＋z，则z的几何意义为直线在y轴上的截距，将目标函数平移可知当直线经过点A时，目标函数取得最大值4，此时A点坐标为(a，a)，代入得4＝a＋a＝‎2a，所以a＝2.‎ 答案　C ‎6．某公司生产甲、乙两种桶装产品．已知生产甲产品1桶需耗A原料‎1千克、B原料‎2千克；生产乙产品1桶需耗A原料‎2千克、B原料‎1千克．每桶甲产品的利润是300元，每桶乙产品的利润是400元．公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12千克．通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是 (　　)．‎ A．1 800元 B．2 400元 C．2 800元 D．3 100元 解析　设某公司生产甲产品x桶，生产乙产品y桶，获利为z元，则x，y满足的线性约束条件为目标函数z＝300x＋400y.‎ 作出可行域，如图中四边形OABC的边界及其内部整点．作直线l0：3x＋4y＝0，平移直线l0经可行域内点B时，z取最大值，由得B(4,4)，满足题意，所以zmax＝4×300＋4×400＝2 800.‎ 答案　C 二、填空题 ‎7．若x，y满足约束条件则z＝3x－y的最小值为________．‎ 解析　画出可行域，如图所示，将直线y＝3x－z移至点A(0,1)处直线在y轴上截距最大，zmin＝3×0－1＝－1.‎ 答案　－1‎ ‎8．若x，y满足约束条件则x－y的取值范围是________．‎ 解析　记z＝x－y，则y＝x－z，所以z为直线y＝x－z在y轴上的截距的相反数，画出不等式组表示的可行域如图中△ABC区域所示．结合图形可知，当直线经过点B(1,1)时，x－y取得最大值0，当直线经过点C(0,3)时，x－y取得最小值－3.‎ 答案　[－3,0]‎ ‎9．设实数x、y满足则的最大值是________．‎ 解析　不等式组确定的平面区域如图阴影部分．‎ 设＝t，则y＝tx，求的最大值，即求y＝tx的斜率的最大值．显然y＝tx过A点时，t最大．‎ 由解得A.‎ 代入y＝tx，得t＝.所以的最大值为.‎ 答案　 ‎10．设m>1，在约束条件下，目标函数z＝x＋my的最大值小于2，则m的取值范围为________．‎ 解析　目标函数z＝x＋my可变为y＝－x＋，‎ ‎∵m>1，∴－1<－<0，z与同时取到相应的最大值，如图，当目标函数经过点P时，取最大值，∴＋<2，又m>1，得1