- 247.50 KB
- 2021-06-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共10页。时量120分钟。满分150分。
得分:______________
第Ⅰ卷
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A=,B=,则∁AB=(B)
A. B.{x|2≤x<5}
C. D.
【解析】∵A={x|10,则方程x2+x-m=0有实根”的逆命题为真命题
D.命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
【解析】C项命题的逆命题为“若方程x2+x-m=0有实根,则m>0”.若方程有实根,则Δ=1+4m≥0,即m≥-,不能推出m>0.所以不是真命题.
3.用二分法求函数f=ln+x-1在区间上的零点,要求精确度为0.01时,所需二分区间的次数最少为(C)
A.5 B.6 C.7 D.8
【解析】开区间的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为,
∵精确度为0.01,∴<0.01,又n∈N*,∴n≥7,故所需二分区间的次数最少为7.选C.
4. △ABC的内角 A、B、C 的对边分别为a、b、c,已知A=,a=6,b=8,则c=(A)
A.4-2 或4+2 B.4-2
C.4+2 D.4
【解析】∵=,∴sin B=>sin,∴B>,故cos B=±,故sin C=,由=得:c=4±2.故选A.
5.已知表示的平面区域为D,若∀(x,y)∈D,2x+y≤a为真命题,则实数a的取值范围是(A)
A.[5,+∞) B.[2,+∞) C.[1,+∞) D.[0,+∞)
【解析】绘制不等式组表示的可行域如图所示,
结合目标函数的几何意义可得目标函数z=2x+y在点B处取得最大值,
联立直线方程可得即B,
则zmax=2×+=5.
结合恒成立的条件可知a≥5,即实数a的取值范围是 [5,+∞).故选A.
6.已知点(1,-2)和在直线l:ax-y-1=0(a≠0)的两侧,则直线l倾斜角的取值范围是(C)
A. B.
C.∪ D.
【解析】∵点(1,-2)和在直线l:ax-y-1=0(a≠0)的两侧,
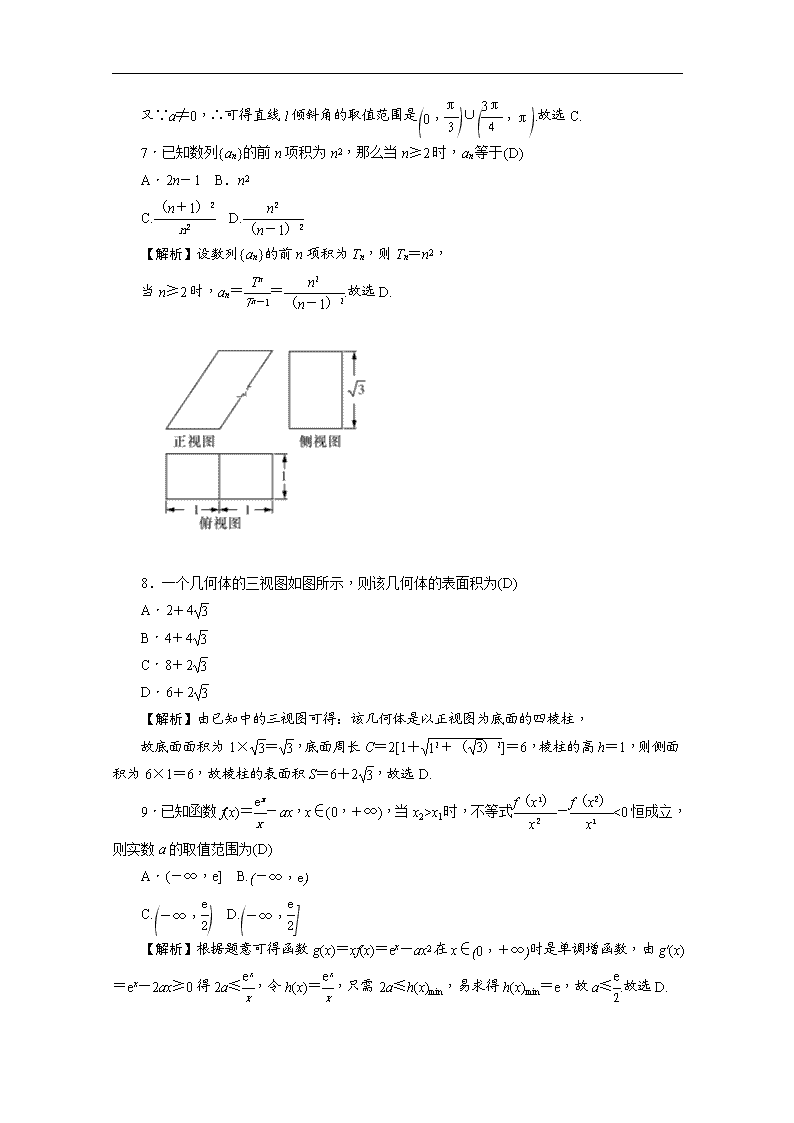
∴(a+2-1)<0,解得-1x1时,不等式-<0恒成立,则实数a的取值范围为(D)
A.(-∞,e] B.
C. D.
【解析】根据题意可得函数g(x)=xf(x)=ex-ax2在x∈时是单调增函数,由g′(x)=ex-2ax≥0得2a≤,令h(x)=,只需2a≤h(x)min,易求得h(x)min=e,故a≤.故选D.
10.如图所示,在
直角梯形ABCD中,AB∥CD,∠DAB=90°,AD =AB=4,CD=1,动点P在边BC上,且满足=m+n(m,n均为正实数),则+的最小值为(B)
A.5 B.+
C. D.
【解析】依题意得DC∥AB,∴=-=-,
∴=m+n=m+n=+n.
∵C,P,B三点共线,
∴+n=1,即m+n=1,
又∵m,n均是正实数,
∴+==++≥+2=+,
当且仅当=,即时,等号成立.选B.
11.定义在R上的偶函数f(x),满足f(x+2)=f(x),且在区间[-3,-2]上是减函数,若A,B是锐角三角形的两个内角,则(A)
A.f(sin A)>f(cos B) B.f(sin A)<f(cos B)
C.f(sin A)>f(sin B) D.f(cos A)>f(cos B)
【解析】因为f(x+2)=f(x),所以函数的周期为2.又因为f(x)在[-3,-2]上为减函数,所以f(x)在[-1,0]上为减函数.因为f(x)为偶函数,所以f(x)在[0,1]上为增函数.
因为在锐角三角形中,A+B>,所以>A>-B>0,所以sin A>sin=cos B.
因为f(x)在[0,1]上为增函数,所以f(sin A)>f(cos B).选A.
12.定义:对于函数y=f(x),x∈D.若存在常数c,对于任意x1∈D,存在唯一的x2∈D,
使得=c,则称函数f(x)在D上的“均值”为c.若f(x)=lg x,x∈[,100],则函数f(x)=lg x在[,100]上的“均值”为(C)
A. B. C. D.10
【解析】假设存在常数c,对于任意x1∈[,100],存在唯一x2∈[,100],
使得=c,即x1x2=102c,则x2=.
故当x1∈[, 100]时,x2∈,又x2∈[,100],
∴从而102c=100,即102c=10 ,
∴c=.故选C.
题 号
1
2
3
4
5
6
7
8
9
10
11
12
答 案
B
C
C
A
A
C
D
D
D
B
A
C
第Ⅱ卷
本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
二、填空题:本大题共4个小题,每小题5分,共20分.把答案填在答题卡中对应题号后的横线上.
13.观察下列式子:1+<,1++<,1+++<,…,根据以上式子可以猜想:1+++…+<____.
14.已知等差数列{an},{bn}的前n项和分别为Sn,Tn,且=,则=____.
【解析】在等差数列中,===,
∵=,
∴===.
15.如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
①MO∥平面PAC;
②PA∥平面MOB;
③OC⊥平面PAC;
④平面PAC⊥平面PBC.
其中正确的命题的序号是__①④__.
【解析】①因为MO∥PA,MO⊄平面PAC,PA⊂平面PAC,所以MO∥平面PAC,①正确;
②因为PA在平面MOB内,所以②错误;
③因为PA垂直于圆O所在的平面,所以PA⊥BC.
又BC⊥AC,AC∩PA=A,所以BC⊥平面PAC.
因为空间内过一点作已知平面的垂线有且只有一条,所以OC⊥平面PAC不成立,③错误;
④由③知BC⊥平面PAC,且BC⊂平面PBC,所以平面PAC⊥平面PBC.
正确命题的序号是①④.
16.已知关于x的方程xln x-a(x2-x)=0在上有两个实数根,则a的取值范围是__(0,1)∪(1,2ln__2)__.
【解析】当x=1时,方程等价为ln 1-a(1-1)=0,即x=1是方程的一个根,
方程xln x-a(x2-x)=0在上有两个实数根等价于函数g(x)=ln x与h(x)=a(x-1)在上有两个交点,显然(1,0)为一个交点,结合g(x)与h(x)的图象,
h(x)=a(x-1)经过点时,a=2ln 2.
h(x)=a(x-1)与g(x)=ln x相切时,a=1,
故当a∈(0,1)∪(1,2ln 2)时,有两个交点.
三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动
不喜好体育运动
男生
5
女生
10
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由;
(Ⅲ)在上述喜好体育运动的6人中随机抽取两人,求恰好抽到一男一女的概率.
参考公式:K2=(n=a+b+c+d).
独立性检验临界值表:
P(K2≥k0)
0.10
0.05
0.025
0.010
k0
2.706
3.841
5.024
6.635
【解析】(Ⅰ)喜好体育运动的人数为:50×=30,列联表补充如下:
喜好体育运动
不喜好体育运动
男生
20
5
女生
10
15
(2分)
(Ⅱ)∵K2=≈8.333>6.635.
∴可以在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关.(7分)
(Ⅲ)6人中有男生4人,设为A1,A2,A3,A4,女生2人,设为B1,B2,
随机抽取两人所有的情况为:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2), 共15种.
其中一男一女包含8种情况,故概率为P=.(12分)
18.(本小题满分12分)
已知数列{an}是公比为3的等比数列,且a2,a3+6,a4成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=an+log3an+1,求数列{bn}的前n项和Tn.
【解析】(Ⅰ)由题意可得2=a2+a4,
即2=3a1+27a1,解得:a1=1.(3分)
∴数列的通项公式为an=3n-1.(5分)
(Ⅱ)bn=an+log3an+1=3n-1+n.(7分)
Tn=b1+b2+b3+…+bn=+
=+=+.(12分)
19.(本小题满分12分)
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(Ⅰ)证明:B1C⊥AB;
(Ⅱ)若AC⊥AB1,∠CBB1=60°,BC=1,求B1到平面ABC的距离.
【解析】(Ⅰ)证明:连接BC1,则O为B1C与BC1的交点,
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,(2分)
∵AO⊥平面BB1C1C,
∴AO⊥B1C,(4分)
∵AO∩BC1=O,
∴B1C⊥平面ABO,
∵AB⊂平面ABO,
∴B1C⊥AB.(6分)
(Ⅱ)作OD⊥BC,垂足为D,连接AD,作OH⊥AD,垂足为H,
∵BC⊥AO,BC⊥OD,AO∩OD=O,
∴BC⊥平面AOD,
∴OH⊥BC,
∵OH⊥AD,BC∩AD=D,
∴OH⊥平面ABC.(8分)
∵∠CBB1=60°,
∴△CBB1为等边三角形,
∵BC=1,∴OD=,
∵AC⊥AB1,∴OA=B1C=,
∴AD==,由OH·AD=OD·OA,∴OH=,
∵O为B1C的中点,
∴B1到平面ABC的距离为.(12分)
20.(本小题满分12分)
已知椭圆C的对称中心为原点O,焦点在x轴上,焦距为2,点(2,1)在该椭圆上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,若为定值,求出此定值;若不为定值,请说明理由.
【解析】(Ⅰ)因为椭圆C的对称中心为原点O,焦点在x轴上,
所以设椭圆方程为+=1,
因为焦距为2,所以c=,
设焦点坐标F1 ,F2,
又因为点在该椭圆上,代入椭圆方程得+=1 ,即+=1,
解得a2=8,所以b2=2,
则椭圆C的方程为+=1.(4分)
(Ⅱ)将x=2代入椭圆方程可得+=1,解得y=±1,
则P,Q.
当点A,B运动时,满足∠APQ=∠BPQ,则直线PA与直线PB的斜率互为相反数,
不妨设kPA=k>0,则kPB=-k(k≠0),(6分)
所以直线PA的方程为y-1=k(x-2),
联立解得x2+x+16k2-16k-4=0,
设A(x1,y1),B(x2,y2),
因为2,x1是该方程的两根,
所以2x1=,即x1=,(8分)
同理直线PB的方程为y=-kx+2k+1,且x2=,
所以x1+x2=,x1-x2=-,
所以kAB===,
即直线AB的斜率为定值.(12分)
21.(本小题满分12分)
已知函数f(x)=mln x-x2(m∈R,m>0).
(Ⅰ)若m=2,求f(x)在(1,f(1))处的切线方程;
(Ⅱ)若y=f(x)在[,e]上有零点,求m的取值范围.
【解析】(Ⅰ)m=2时,f=-,f′=-x,
∴f′=1.故所求切线方程为y+=x-1,即2x-2y-3=0.(4分)
(Ⅱ)依题意f′=-x=,
①当00,此时函数y=f(x)无零点).(8分)
③当e0,f(x)单调递增,
若x∈(,e],f′(x)<0,f单调递减,
由m>e时,f()=>0.
故只需f(e)≤0,即m-e2≤0,又e≤,
故此时e0,t2>0,
由参数t的几何意义可知,=,=,
所以+=+=+ ==.(10分)
23.(本小题满分10分)选修4—5: 不等式选讲
已知函数f(x)=+.
(Ⅰ)若f(x)的最小值为3,求实数a的值;
(Ⅱ)若a=2时,不等式f(x)≤4的解集为A,当m,n∈A时,求证:≥2.
【解析】(Ⅰ)因为f=+≥ =,
当且仅当≤0时取“=”号,
所以=3,解得a=1或-5.(5分)
(Ⅱ)当a=2时,f=+=
当x<-2时,由f≤4,得-2x≤4,解得x≥-2,又x<-2,所以不等式无实数解;
当-2≤x<2时,f≤4恒成立,所以-2≤x<2;
当x≥2时,由f≤4,得2x≤4,解得x=2;
所以f≤4的解集为A={x|-2≤x≤2}.
-4=-4
=m2n2+16-4m2-4n2=+ =.
因为m,n∈,所以≤0,≤0,所以-4≥0,
即≥4,所以≥2.(10分)