2018年黑龙江省大庆市高考数学一模试卷（理科） 25页

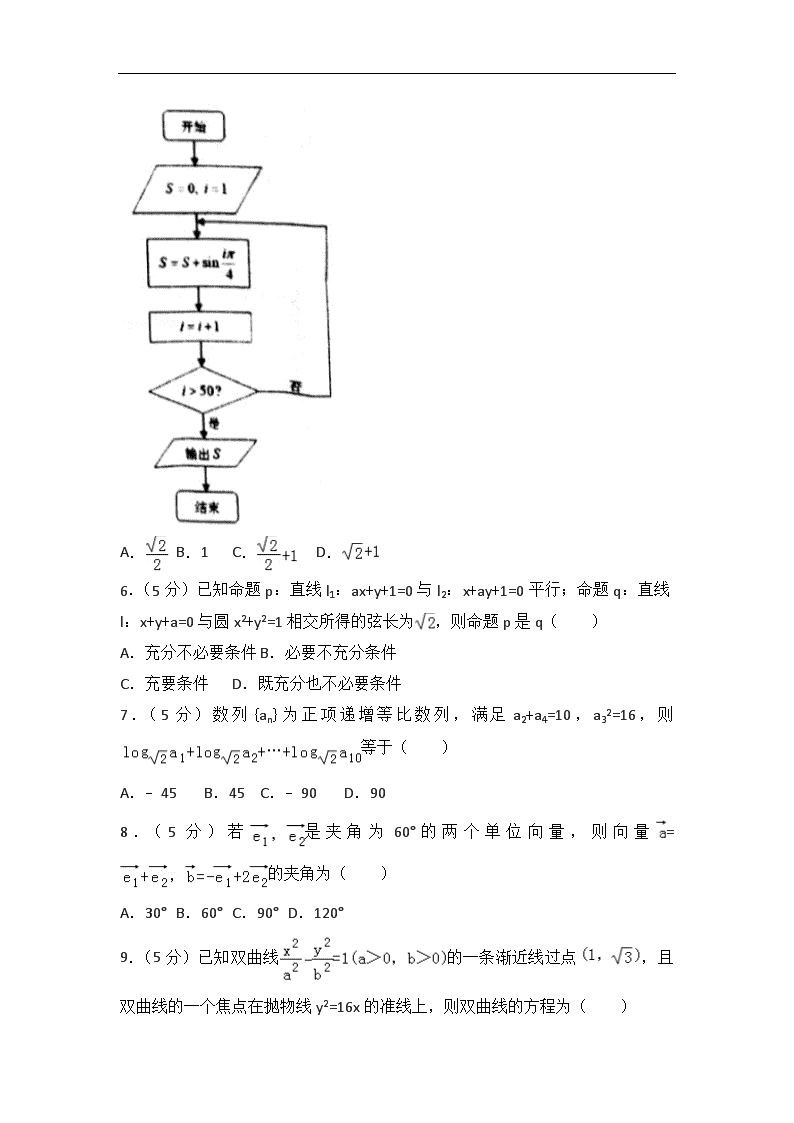
‎2018年黑龙江省大庆市高考数学一模试卷（理科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）设集合A={﹣1，0，1，2，3}，B={x||x|≤2}，则A∩B=的值为（　　）‎ A．{﹣1，0，1，2} B．{﹣2，﹣1，0，1，2} C．{0，1，2} D．{1，2}‎ ‎2．（5分）若复数，则z在复平面内所对应的点位于的（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3．（5分）若x，y满足，则2x+y的最大值为（　　）‎ A．2 B．5 C．6 D．7‎ ‎4．（5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几伺体的三视图，则此几何体的体积为（　　）‎ A．2 B．4 C．8 D．12‎ ‎5．（5分）执行如图所示的程序语句，则输出的s的值为（　　）‎ A． B．1 C． D．‎ ‎6．（5分）已知命题p：直线l1：ax+y+1=0与l2：x+ay+1=0平行；命题q：直线l：x+y+a=0与圆x2+y2=1相交所得的弦长为，则命题p是q（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既充分也不必要条件 ‎7．（5分）数列{an}为正项递增等比数列，满足a2+a4=10，a32=16，则等于（　　）‎ A．﹣45 B．45 C．﹣90 D．90‎ ‎8．（5分）若是夹角为60°的两个单位向量，则向量=的夹角为（　　）‎ A．30° B．60° C．90° D．120°‎ ‎9．（5分）已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线y2=16x的准线上，则双曲线的方程为（　　）‎ A． B． C． D．‎ ‎10．（5分）已知f（x）是定义在R上的奇函数，当x∈[0，+∞）时，f′（x）＜0．若，，则a，b，c的大小关系为（　　）‎ A．b＜a＜c B．b＜c＜a C．c＜a＜b D．a＜c＜b ‎11．（5分）函数f（x）=2sin（ωx+ϕ）的图象过点，相邻两个对称中心的距离是，则下列说法不正确的是（　　）‎ A．f（x）的最小正周期为 B．f（x）的一条对称轴为 C．f（x）的图象向左平移个单位所得图象关于y轴对称 D．f（x）在上是减函数 ‎12．（5分）已知函数，若关于x的方程f（x）﹣ax=0有两个解，则实数a的取值范围是（　　）‎ A． B．‎ C． D．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）　 　．‎ ‎14．（5分）一个圆柱的轴截面是正方形，在圆柱内有一个球O，该球与圆柱的上、下底面及母线均相切．记球O的体积为V1，圆柱内除了球之外的几何体体积记为V2，则的值为　 　．‎ ‎15．（5分）若f（x）=exlna+e﹣xlnb为奇函数，则的最小值为　 　．‎ ‎16．（5分）已知抛物线C：y2=4x，过其焦点F作一条斜率大于0的直线l，l与抛物线交于M，N两点，且|MF|=3|NF|，则直线l的斜率为　 　．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）设函数y=f（x）的图象由y=2sin2x+1的图象向左平移个单位得到．‎ ‎（1）求f（x）的最小正周期及单调递增区间：‎ ‎（2）在△ABC中，a，b，c，6分别是角A，B，C的对边，且f（A）=2，b=1，，求a的值．‎ ‎18．（12分）已知数列{an}的前n项和为sn，点（n，sn）在曲线，上数列{bn}满足bn+bn+2=2bn+1，b4=11，{bn}的前5项和为45．‎ ‎（1）求{an}，{bn}的通项公式；‎ ‎（2）设，数列{cn}的前n项和为Tn，求使不等式恒成立的最大正整数k的值．‎ ‎19．（12分）已知四棱锥P﹣ABCD的底面ABCD为正方形，PA⊥上面ABCD且PA=AB=2．E为PA的中点．‎ ‎（1）求证：PC∥面BDE；‎ ‎（2）求直线DE与平面PBC所成角的余弦值．‎ ‎20．（12分）已知椭圆（a＞b＞0），其焦距为2，离心率为 ‎（1）求椭圆C的方程；‎ ‎（2）设椭圆的右焦点为F，K为x轴上一点，满足 ‎，过点K作斜率不为0的直线l交椭圆于P，Q两点，求△FPQ面积s的最大值．‎ ‎21．（12分）已知函数f（x）=1﹣ax+lnx ‎（1）若不等式f（x）≤0恒成立，则实数a的取值范围；‎ ‎（2）在（1）中，a取最小值时，设函数g（x）=x（1﹣f（x））﹣k（x+2）+2．若函数g（x）在区间上恰有两个零点，求实数k的取值范围；‎ ‎（3）证明不等式：（n∈N*且n≥2）．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]‎ ‎22．（10分）在平面直角坐标系xoy中，以原点O为极点，x轴正半轴为极轴，取相同的单位长度建立极坐标系，已知曲线，直线l：ρ（cosθ﹣sinθ）=4．‎ ‎（1）将曲线C1上所有点的横坐标、纵坐标分别伸长为原来的2倍、倍后得到曲线C2，请写出直线l，和曲线C2的直角坐标方程；‎ ‎（2）若直线l1经过点P（1，2）且l1∥l，l1与曲线C2交于点M，N，求|PM|•|PN|的值．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知a，b是任意非零实数．‎ ‎（1）求的最小值 ‎（2）若不等式|3a+2b|+|3a﹣2b|≥|a|（|2+x|+|2﹣x|）恒成立，求实数x取值范圈．‎ ‎　‎ ‎2018年黑龙江省大庆市高考数学一模试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）设集合A={﹣1，0，1，2，3}，B={x||x|≤2}，则A∩B=的值为（　　）‎ A．{﹣1，0，1，2} B．{﹣2，﹣1，0，1，2} C．{0，1，2} D．{1，2}‎ ‎【解答】解：∵集合A={﹣1，0，1，2，3}，B={x||x|≤2}={x|﹣2≤x≤2}，‎ ‎∴A∩B={﹣1，0，1，2}．‎ 故选：A．‎ ‎　‎ ‎2．（5分）若复数，则z在复平面内所对应的点位于的（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【解答】解：∵=，‎ ‎∴复数z在复平面内所对应的点的坐标为（，﹣），位于第四象限．‎ 故选：D．‎ ‎　‎ ‎3．（5分）若x，y满足，则2x+y的最大值为（　　）‎ A．2 B．5 C．6 D．7‎ ‎【解答】解：作出x，y满足对应的平面区域如图：（阴影部分）．‎ 由z=2x+y得y=﹣2x+z，‎ 平移直线y=﹣2x+z，‎ 由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最大，‎ 此时z最大．‎ 由，解得A（2，1），‎ 代入目标函数z=2x+y得z=2×2+1=5．‎ 即目标函数z=2x+y的最大值为5．‎ 故选：B．‎ ‎　‎ ‎4．（5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几伺体的三视图，则此几何体的体积为（　　）‎ A．2 B．4 C．8 D．12‎ ‎【解答】解：由几何体的三视图得到该几何体是四棱锥S﹣ABCD，‎ 其中，四边形ABCD是边长为2的正方形，‎ PD⊥平面ABCD，PD=3，‎ ‎∴几何体的体积：‎ V=‎ ‎=‎ ‎=4．‎ 故选：B．‎ ‎　‎ ‎5．（5分）执行如图所示的程序语句，则输出的s的值为（　　）‎ A． B．1 C． D．‎ ‎【解答】解：模拟程序框图的运行过程，得出该程序运行后输出的是S=sin+sin ‎+sin+…+sin的值，‎ S=sin+sin+sin+…+sin ‎=（sin+sin+sin+…+sin）+…sin+sin ‎=sin+sin ‎=sin+sin ‎=1+．‎ 故选：C．‎ ‎　‎ ‎6．（5分）已知命题p：直线l1：ax+y+1=0与l2：x+ay+1=0平行；命题q：直线l：x+y+a=0与圆x2+y2=1相交所得的弦长为，则命题p是q（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既充分也不必要条件 ‎【解答】解：当a=0时，两直线方程分别为y+1=0，x+1=0，两直线不平行，‎ 当a≠0时，若两直线平行，则满足=≠，‎ 由=得a2=1，得a=±1，由≠，得a≠1，即a=﹣1，‎ 即p：a=﹣1，‎ 圆心到直线的距离d=，半径r=1，‎ ‎∵直线l：x+y+a=0与圆x2+y2=1相交所得的弦长为，‎ ‎∴r2=d2+（）2，‎ 即1=+，得a2=1，得a=±1，‎ 则命题p是q充分不必要条件，‎ 故选：A．‎ ‎　‎ ‎7．（5分）数列{an}为正项递增等比数列，满足a2+a4=10，a32=16，则等于（　　）‎ A．﹣45 B．45 C．﹣90 D．90‎ ‎【解答】解：因为{an}为正项递增等比数列，所以an＞an﹣1＞0，公比q＞1．‎ ‎ 因为a2+a4=10 ①，且=16=a3•a3=a2•a4②‎ ‎ 由①②解得a2=2，a4=8．又因为 a4=a2•q2，得q=2或q=﹣2（舍）．则得a5=16，a6=32，‎ ‎ 因为++…+==5=5=5×9=45×2=90，‎ 故选：D ‎　‎ ‎8．（5分）若是夹角为60°的两个单位向量，则向量=的夹角为（　　）‎ A．30° B．60° C．90° D．120°‎ ‎【解答】解：根据题意，设、的夹角为θ，‎ 又由是夹角为60°的两个单位向量，且=，‎ 则•=（+）（﹣+2）=﹣2+22+•=，‎ 又由=（+），则||==，‎ ‎=（﹣+2），则||==，‎ 则有cosθ==，‎ 则θ=60°；‎ 故选：B．‎ ‎　‎ ‎9．（5分）已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线y2=16x的准线上，则双曲线的方程为（　　）‎ A． B． C． D．‎ ‎【解答】解：双曲线的渐近线方程为y=±x，‎ 由一条渐近线过点，可得=，‎ 双曲线的一个焦点（﹣c，0）在抛物线y2=16x的准线x=﹣4上，‎ 可得c=4，‎ 即有a2+b2=16，‎ 解得a=2，b=2，‎ 则双曲线的方程为﹣=1．‎ 故选：A．‎ ‎　‎ ‎10．（5分）已知f（x）是定义在R上的奇函数，当x∈[0，+∞）时，f′（x）＜0．若，，则a，b，c的大小关系为（　　）‎ A．b＜a＜c B．b＜c＜a C．c＜a＜b D．a＜c＜b ‎【解答】解：∵当x∈[0，+∞）时，f′（x）＜0，‎ ‎∴当x∈[0，+∞）时，函数f（x）单调递减，‎ ‎∵f（x）是定义在R上的奇函数，∴函数在（﹣∞，+∞）上单调递减，‎ a=﹣f（ln）=﹣f（﹣ln2）=f（ln2），‎ ln（﹣）＞ln=﹣1，又ln（﹣）＜0，‎ 则﹣1＜ln（﹣）＜0，e0.1＞1，0＜ln2＜1，‎ 则﹣1＜ln（﹣）＜ln2＜e0.1，‎ 则f（ln（﹣））＞f（ln2）＞f（e0.1），‎ 即c＜a＜b，‎ 故选：C．‎ ‎　‎ ‎11．（5分）函数f（x）=2sin（ωx+ϕ）的图象过点，相邻两个对称中心的距离是，则下列说法不正确的是（　　）‎ A．f（x）的最小正周期为 B．f（x）的一条对称轴为 C．f（x）的图象向左平移个单位所得图象关于y轴对称 D．f（x）在上是减函数 ‎【解答】解：函数f（x）=2sin（ωx+φ）图象相邻两个对称中心的距离是，‎ ‎∴=，∴T==，解得ω=3；‎ 又f（x）的图象过点，‎ ‎∴2sin（ω+φ）=2，‎ ‎∴ω+φ=+2kπ，k∈Z；‎ 解得φ=+2kπ，k∈Z；‎ 令k=0，得φ=，‎ ‎∴f（x）=2sin（3x+）；‎ ‎∴f（x）的最小正周期为T=，A正确；‎ f（）=2sin（3×+）=﹣2为最小值，‎ ‎∴f（x）的一条对称轴为x=，B正确；‎ f（x）的图象向左平移个单位，‎ 得函数y=2sin[3（x+）+]=2sin（3x+）=2cos3x，‎ 其图象关于y轴对称，C正确；‎ x∈[﹣，]时，3x∈[﹣，]，‎ ‎∴3x+∈[﹣，]时，‎ ‎∴f（x）=2sin（3x+）在上是增函数，D错误．‎ 故选：D．‎ ‎　‎ ‎12．（5分）已知函数，若关于x的方程f（x）﹣ax=0有两个解，则实数a的取值范围是（　　）‎ A． B．‎ C． D．‎ ‎【解答】解：设函数y=f（x）和y=ax，‎ 作出函数f（x）的图象如图：‎ 要使方程f（x）﹣ax=0有2两个解，‎ 即函数y=f（x）和y=ax有2个不同的交点，‎ ‎∵f（﹣2）=5，f（5）=|5+﹣4|=，‎ 当y=ax经过点（5，）时，此时a=，‎ 当过点（﹣2，5）时，此时a=﹣，‎ 当直线y=ax与y=x2+1相切时，‎ ‎∵y′=2x，设切点为（x0，y0），﹣2≤x0≤0，‎ ‎∴=2x0，‎ 解得x0=﹣1，‎ 当x0=﹣1，此时a=﹣2，‎ 结合图象，综上所述a的取值范围为[﹣，﹣2）∪（0，]，‎ 故选：A ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）　6　．‎ ‎【解答】解：（2x﹣1）dx=（x2﹣x）=9﹣3=6，‎ ‎∴（2x﹣1）dx=6，‎ 故答案为：6‎ ‎　‎ ‎14．（5分）一个圆柱的轴截面是正方形，在圆柱内有一个球O，该球与圆柱的上、下底面及母线均相切．记球O的体积为V1，圆柱内除了球之外的几何体体积记为V2，则的值为　2　．‎ ‎【解答】解：设圆柱的底面半径为r，‎ 则圆柱的高为2r，球O的半径为r，‎ ‎∴球O的体积V1=，‎ 圆柱内除了球之外的几何体体积：‎ V2==，‎ ‎∴==2．‎ 故答案为：2．‎ ‎　‎ ‎15．（5分）若f（x）=exlna+e﹣xlnb为奇函数，则的最小值为　2　．‎ ‎【解答】解：f（x）=exlna+e﹣xlnb为奇函数，‎ 可得f（0）=0，‎ 即有e0lna+e0lnb=0，‎ 即有ln（ab）=0，‎ 可得ab=1，（a＞0，b＞0），‎ 则≥2=2，‎ 当且仅当b=2a=时，等号成立，‎ 则的最小值为2．‎ 故答案为：2．‎ ‎　‎ ‎16．（5分）已知抛物线C：y2=4x，过其焦点F作一条斜率大于0的直线l，l与抛物线交于M，N两点，且|MF|=3|NF|，则直线l的斜率为　　．‎ ‎【解答】解：抛物线C：y2=4x，焦点F（1，0），准线为x=﹣1，‎ 分别过M和N作准线的垂线，垂足分别为C和D，‎ 过NH⊥CM，垂足为H，‎ 设|NF|=x，则|MF|=3x，‎ 由抛物线的定义可知：|NF|=|DH|=x，|MF|=|CM|=3x，‎ ‎∴|HM|=2x，由|MN|=4x，‎ ‎∴∠HMF=60°，则直线MN的倾斜角为60°，‎ 则直线l的斜率k=tan60°=，‎ 故答案为：．‎ 方法二：抛物线C：y2=4x，焦点F（1，0），‎ 准线为x=﹣1，‎ 设直线MN的斜率为k，则直线MN的方程y=k（x﹣1），‎ 设M（x1，y1），N（x2，y2），‎ ‎，整理得：k2x2﹣2（k2+2）x+k2=0，则x1+x2=，x1x2=1，‎ 由|MF|=3|NF|，=3，即（1﹣x1，﹣y1）=3（x2﹣1，y2），‎ x1+3x2=4，整理得：3x2﹣4x2+1=0，解得：x2=，或x2=1（舍去），‎ 则x1=3，解得：k=±，‎ 由k＞0，则k=‎ 故答案为：．‎ 方法三：抛物线C：y2=4x，焦点F（1，0），准线为x=﹣1，‎ 设直线MN的方程x=mx+1，设M（x1，y1），N（x2，y2），‎ ‎，整理得：y2﹣4my﹣4=0，则y1+y2=4m，y1y2=﹣4，‎ 由|MF|=3|NF|，=3，即（1﹣x1，﹣y1）=3（x2﹣1，y2），‎ ‎﹣y1=3y2，即y1=﹣3y2，解得：y2=﹣，y1=2，‎ ‎∴4m=，则m=，‎ ‎∴直线l的斜率为，‎ 故答案为：．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）设函数y=f（x）的图象由y=2sin2x+1的图象向左平移个单位得到．‎ ‎（1）求f（x）的最小正周期及单调递增区间：‎ ‎（2）在△ABC中，a，b，c，6分别是角A，B，C的对边，且f（A）=2，b=1，，求a的值．‎ ‎【解答】解：（1）y=2sin2x+1的图象向左平移个单位得到的图象，‎ 即．‎ 函数最小正周期T=π．‎ 令 ，‎ 则 ，‎ 解得，‎ 所以y=f（x）的单调增区间是．‎ ‎（2）由题意得：，则有．‎ 因为0＜A＜π，所以，．‎ 由及b=1得，c=4．‎ 根据余弦定理，，‎ 所以．‎ ‎　‎ ‎18．（12分）已知数列{an}的前n项和为sn，点（n，sn）在曲线，上数列{bn}满足bn+bn+2=2bn+1，b4=11，{bn}的前5项和为45．‎ ‎（1）求{an}，{bn}的通项公式；‎ ‎（2）设，数列{cn}的前n项和为Tn，求使不等式恒成立的最大正整数k的值．‎ ‎【解答】解：（1）由已知得：，‎ 当n=1时，，‎ 当n≥2时，=n+2，‎ 当n=1时，符合上式．‎ 所以an=n+2．‎ 因为数列{bn}满足bn+bn+2=2bn+1，所以{bn}为等差数列．设其公差为d．‎ 则，解得，‎ 所以bn=2n+3．‎ ‎（2）由（1）得，=，=，‎ 因为，‎ 所以{Tn}是递增数列．‎ 所以，‎ 故恒成立只要恒成立．‎ 所以k＜9，最大正整数k的值为8．‎ ‎　‎ ‎19．（12分）已知四棱锥P﹣ABCD的底面ABCD为正方形，PA⊥上面ABCD且PA=AB=2．E为PA的中点．‎ ‎（1）求证：PC∥面BDE；‎ ‎（2）求直线DE与平面PBC所成角的余弦值．‎ ‎【解答】（1）解：连接CA交BD于O，连接OE，‎ 因为ABCD为正方形且AC，BD为对角线，‎ 所以O为CA的中点，‎ 又E为PA的中点，‎ 故OE为△PAC的中位线，‎ 所以OE∥PC，‎ 而OE⊂面BDE，PC⊄面BDE，‎ 故PC∥面BDE．‎ ‎（2）以A为原点，AB，AD，AP所在直线分别为x，y，z轴建立空间直角坐标系A﹣xyz．‎ 则B（2，0，0），D（0，2，0），C（2，2，0），E（0，0，1），P（0，0，2），‎ 所以，，，‎ 设平面PBC的法向量，则即，‎ 令z=1，则法向量，‎ 设直线DE与平面PBC所成角为θ，‎ 则，‎ 故直线DE与平面PBC所成角的余弦值．‎ ‎　‎ ‎20．（12分）已知椭圆（a＞b＞0），其焦距为2，离心率为 ‎（1）求椭圆C的方程；‎ ‎（2）设椭圆的右焦点为F，K为x轴上一点，满足，过点K作斜率不为0的直线l交椭圆于P，Q两点，求△FPQ面积s的最大值．‎ ‎【解答】解：（1）因为椭圆焦距为2，即2c=2，所以c=1，，所以a=，‎ 从而b2=a2﹣c2=1，‎ 所以，椭圆的方程为+y2=1．‎ ‎（2）椭圆右焦点F（1，0），由可知K（2，0），‎ 直线l过点K（2，0），设直线l的方程为y=k（x﹣2），k≠0，‎ 将直线方程与椭圆方程联立得（1+2k2）x2﹣8k2x+8k2﹣2=0．‎ 设P（x1，y1），Q（x2，y2），则，，‎ 由判别式△=（﹣8k2）2﹣4（2k2+1）（8k2﹣2）＞0解得k2＜．‎ 点F（1，0）到直线l的距离为h，则，‎ ‎，‎ ‎=••，‎ ‎=|k|•，‎ ‎=，‎ 令t=1+2k2，则1＜t＜2，‎ 则S=•=，‎ 当时，S取得最大值．‎ 此时，，‎ S取得最大值．‎ ‎　‎ ‎21．（12分）已知函数f（x）=1﹣ax+lnx ‎（1）若不等式f（x）≤0恒成立，则实数a的取值范围；‎ ‎（2）在（1）中，a取最小值时，设函数g（x）=x（1﹣f（x））﹣k（x+2）+2．若函数g（x）在区间上恰有两个零点，求实数k的取值范围；‎ ‎（3）证明不等式：（n∈N*且n≥2）．‎ ‎【解答】解：（1）由题意知，1﹣ax+lnx≤0恒成立．变形得：．‎ 设，则a≥h（x）max．‎ 由可知，h（x）在（0，1）上单调递增，在（1，+∞）上单调递减，‎ h（x）在x=1处取得最大值，且h（x）max=h（1）=1．‎ 所以a≥h（x）max=1，‎ 实数a的取值范围是[1，+∞）．‎ ‎（2）由（1）可知，a≥1，当a=1时，f（x）=1﹣x+lnx，‎ g（x）=x（x﹣lnx）﹣k（x+2）+2=x2﹣xlnx﹣k（x+2）+2，‎ g（x）在区间上恰有两个零点，‎ 即关于x的方程x2﹣xlnx﹣k（x+2）+2=0在区间上恰有两个实数根．‎ 整理方程得，，‎ 令，‎ ‎．‎ 令φ（x）=x2+3x﹣2lnx﹣4，，‎ 则，，‎ 于是φ'（x）≥0，φ（x）在上单调递增．‎ 因为φ（1）=0，当时，φ（x）＜0，从而s'（x）＜0，s（x）单调递减，‎ 当x∈（1，8]时，φ（x）＞0，从而s'（x）＞0，s（x）单调递增，‎ ‎，s（1）=1，，‎ 因为，‎ 所以实数k的取值范围是．‎ 证明（3）由（1）可知，当a=1时，有x﹣1≥lnx，‎ 当且仅当x=1时取等号．‎ 令，则有，其中k∈N*，k≥2．‎ 整理得：，‎ 当k=2，3，…，n时，，，…，，‎ 上面n﹣1个式子累加得：．n∈N*且n≥2，‎ 即．命题得证．‎ ‎　‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]‎ ‎22．（10分）在平面直角坐标系xoy中，以原点O为极点，x轴正半轴为极轴，取相同的单位长度建立极坐标系，已知曲线，直线l：ρ（cosθ﹣sinθ）=4．‎ ‎（1）将曲线C1上所有点的横坐标、纵坐标分别伸长为原来的2倍、倍后得到曲线C2，请写出直线l，和曲线C2的直角坐标方程；‎ ‎（2）若直线l1经过点P（1，2）且l1∥l，l1与曲线C2交于点M，N，求|PM|•|PN|的值．‎ ‎【解答】解：（1）因为l：ρ（cosθ﹣sinθ）=4，转化为直角坐标方程为：x﹣y=4；‎ 设曲线C2上任一点坐标为（x'，y'），‎ 则，‎ 所以，‎ 代入C1方程得：，‎ 所以C2的方程为．‎ ‎（2）直线l：x﹣y=4倾斜角为，由题意可知，‎ 直线l1的参数方程为（t为参数），‎ 联立直线l1和曲线C2的方程得，‎ ‎．‎ 设方程的两根为t1，t2，‎ 则t1t2=2．‎ 由直线参数t的几何意义可知，|PM|•|PN|=|t1t2|=2．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知a，b是任意非零实数．‎ ‎（1）求的最小值 ‎（2）若不等式|3a+2b|+|3a﹣2b|≥|a|（|2+x|+|2﹣x|）恒成立，求实数x取值范圈．‎ ‎【解答】解：（1）因为|3a+2b|+|3a﹣2b|≥|3a+2b+3a﹣2b|=6|a|，‎ 当且仅当（3a+2b）（3a﹣2b）≥0时取等号，‎ 所以的最小值为6．‎ ‎（2）由题意得：恒成立，‎ 结合（Ⅰ）得：|2+x|+|2﹣x|≤6．‎ 当x≤﹣2时，﹣x﹣2+2﹣x≤6，解得﹣3≤x≤﹣2；‎ 当﹣2＜x≤2时，x+2+2﹣x≤6成立，所以﹣2＜x≤2；‎ 当x＞2时，x+2+x﹣2≤6，解得2＜x≤3．‎ 综上，实数x的取值范围是[﹣3，3]．‎ ‎　‎