山东省济宁市嘉祥一中2019-2020学年高一6月月考数学试题 9页

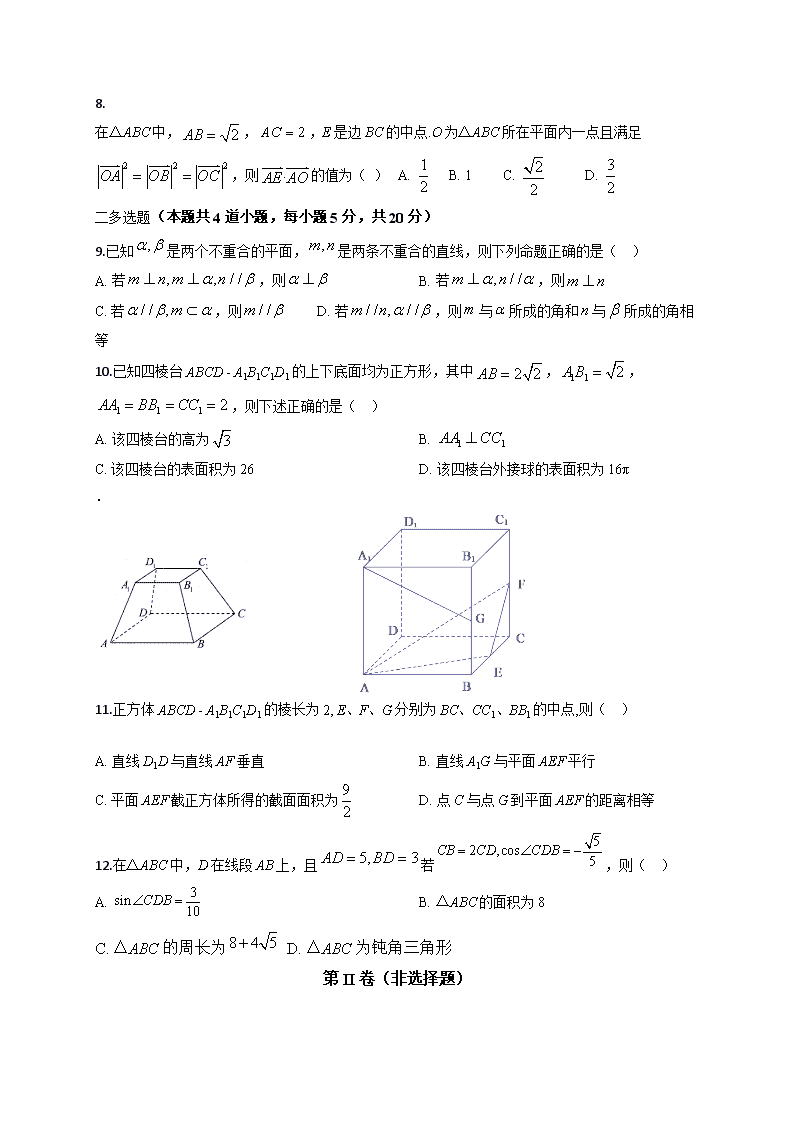
‎2019---2020学年度第二学期检测考试 高一数学试题 ‎ 第I卷（选择题）‎ 一、选择题（本题共8道小题，每小题5分，共40分）‎ ‎1.设向量 ＝（2，4）与向量 ＝（x，6）共线，则实数x＝（ ）‎ A. 2 B. ‎3 ‎C. 4 D. 6‎ ‎2.设向量，若，则实数（ ）‎ A. ±1 B. ‎0 ‎C. D. ±2‎ ‎3.已知直线l是平面的斜线，则内不存在与l（   ）‎ A. 相交的直线 B. 平行的直线 C. 异面的直线 D. 垂直的直线 ‎4.在△ABC中，点D满足，则（ ）‎ A. B. C. D. ‎ ‎5.在△ABC中，为BC的三等分点，则( )‎ A. B. C. D. ‎ ‎6.‎ 在如图的正方体中，M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )‎ A. 30° B. 45° C. 60° D. 90°‎ ‎7.在△ABC中，边a，b，c分别是角A，B，C的对边，且满足，若，则ac的值为 A. 12 B. ‎11 ‎ C. 10 D. 9‎ ‎8.‎ 在△ABC中，，，E是边BC的中点.O为△ABC所在平面内一点且满足，则的值为（ ） A. B. 1 C. D. ‎ 二多选题（本题共4道小题，每小题5分，共20分）‎ ‎9.已知是两个不重合的平面，是两条不重合的直线，则下列命题正确的是（ ）‎ A. 若，则 B. 若，则 C. 若，则 D. 若，则与所成的角和与所成的角相等 ‎10.已知四棱台ABCD - A1B‎1C1D1的上下底面均为正方形，其中，，，则下述正确的是（ ）‎ A. 该四棱台的高为 B. ‎ C. 该四棱台的表面积为26 D. 该四棱台外接球的表面积为16π ‎．‎ ‎ ‎ ‎11.正方体ABCD - A1B‎1C1D1的棱长为2, E、F、G分别为BC、CC1、BB1的中点,则（ ）‎ A. 直线D1D与直线AF垂直 B. 直线A‎1G与平面AEF平行 C. 平面AEF截正方体所得的截面面积为 D. 点C与点G到平面AEF的距离相等 ‎12.在△ABC中，D在线段AB上，且若，则（ ）‎ A. B. △ABC的面积为8‎ C. △ABC的周长为 D. △ABC为钝角三角形 第II卷（非选择题）‎ 三、填空题（本题共4道小题，每小题5分，共20分）‎ ‎13.已知，，若和的夹角为钝角，则的取值范围是______ .‎ ‎14.在《九章算术》中，将四个面都是直角三角形的四面体称之为鳖臑，在鳖臑A-BCD中，AB⊥平面BCD，且有，则此鳖臑的外接球O（A、B、C、D均在球O表面上）的直径为__________；过BD的平面截球O所得截面面积的最小值为__________.‎ ‎15.如图，P为△ABC内一点，且，延长BP交AC于点E，若，则实数的值为_______.‎ ‎16.已知，向量的夹角为，则的最大值为_____.　‎ 三、解答题（本题共6道小题,,共70分）‎ ‎17. 10分 ‎ 已知:‎ ‎（1）若，求的坐标；‎ ‎（2）若与的夹角为120°，求.‎ ‎18.12分 如图，在四棱锥P‐ABCD中，四边形ABCD为正方形，PA⊥平面ABCD，E为PD的中点．‎ ‎ 求证：（1）PB∥平面AEC；‎ ‎（2）平面PCD⊥平面PAD．‎ ‎19. 12分 已知△ABC的角A、B、C所对的边分别是a、b、c，设向量，‎ ‎，.‎ ‎（1）若，求证：△ABC为等腰三角形；‎ ‎（2）若，边长，角，求△ABC的面积.‎ ‎20. 12分 在△ABC中，，，且△ABC的面积为．‎ ‎（1）求a的值；‎ ‎（2）若D为BC上一点，且 ，求的值．‎ 从①，②这两个条件中任选一个，补充在上面问题中并作答．‎ ‎21. 12分 如图，在四棱锥P-ABCD中，PD⊥平面ABCD，，∠ABC=∠BCD=90°，E为PB的中点。‎ ‎（1）证明：CE∥面PAD ‎（2）若直线CE与底面ABCD所成的角为45°，求四棱锥P-ABCD的体积。‎ ‎22. 12分 如图半圆O的直径为4，A为直径MN延长线上一点，且，B为半圆周上任一点，以AB为边作等边△ABC（A、B、C按顺时针方向排列）‎ ‎（1）若等边△ABC边长为a，，试写出a关于的函数关系；‎ ‎（2）问为多少时，四边形的面积最大？这个最大面积为多少？‎ 试卷答案 ‎1.B 2.C 3 .B 4.D 5.B 6.C 7.A 8.D 9.BCD 10.AD 11.BC 12.BCD ‎13.且 14. 3 π 15 . 16.‎ ‎17. 解析：（1）∵，∴，与共线的单位向量为.‎ ‎∵，∴或.‎ ‎（2）∵，∴，‎ ‎∴，∴.‎ ‎18.【详解】（ 1）证明： 连交于O, ‎ 因为四边形是正方形 ,‎ 所以 ,‎ 连，则是三角形的中位线, ,‎ 平面，平面 ‎ 所以平面 . ‎ ‎（2）因为平面 ,‎ 所以 , ‎ 因为是正方形，所以, ‎ 所以平面, ‎ 所以平面平面.‎ ‎19.【详解】⑴因为，所以，即,其中是的外接圆半径， 所以，所以为等腰三角形.‎ ‎⑵因为，所以.‎ 由余弦定理可知，，即 解方程得：（舍去）‎ 所以.‎ ‎20.【详解】（1） 由于 ，，，‎ 所以，‎ 由余弦定理 ，‎ 解得．‎ ‎（2）①当时，‎ 在中，由正弦定理， ‎ 即，所以． ‎ 因为，所以． ‎ 所以， ‎ 即． ‎ ‎②当时，‎ 在中，由余弦定理知，‎ ‎． ‎ 因为，所以， ‎ 所以， ‎ 所以 ， ‎ 即．‎ ‎21.【详解】解法一:(1)取PA中点Q，连接QD，QE， ‎ 则QE∥AB，且QE=AB ‎∴QE∥CD，且QE=CD.‎ 即四边形CDQE为平行四边形，CE∥QD.‎ 又∵CE平面PAD，QD平面PAD，‎ ‎∴CE∥平面PAD.‎ ‎(2)连接BD，取BD中点O，连接EO，CO 则EO∥PD，且EO=PD. ‎ ‎∵PD⊥平面ABCD，‎ ‎∴EO⊥平面ABCD. ‎ 则CO为CE在平面ABCD上的射影，‎ 即∠ECO为直线CE与底面ABCD所成的角，∠ECO=45° ‎ 在等腰直角三角形BCD中，BC=CD=2，则BD=2，‎ 则在RtΔECO中，∠ECO=45°，EO=CO=BD=‎ ‎2PD=2E0=2，‎ ‎∴ ‎ ‎∴ ‎ ‎∴四棱锥P-ABCD的体积为.‎ 解法二：(1)取AB中点Q，连接QC，QE 则QE∥PA ‎∵PA平面PAD，QE平面PAD ‎∴QE∥平面PAD， ‎ 又∵AQ=AB=CD，AQ∥CD，‎ ‎∴四边形AQCDカ平行四迹形，‎ 则CQ∥DA ‎∵DA平面PAD，CQ平面PAD，‎ ‎∴CQ∥平面PAD， ‎ ‎ (QE∥平面PAD.CQ∥平面PAD，证明其中一个即给2分)‎ 又QE平面CEQ，CQ平面CEQ，QECQ=Q，‎ ‎∴平面CEQ∥平面PAD， ‎ 又CE平面CQ，‎ ‎∴CE∥平面PAD. (2)同解法一.‎ ‎22.‎ ‎【详解】（1）由余弦定理得 则 ‎ ‎（2）四边形OACB的面积＝△OAB的面积+△ABC的面积 则△ABC的面积 ‎△OAB的面积•OA•OB•sinθ•2•4•sinθ＝4sinθ 四边形OACB的面积4sinθ=‎ sin（θ﹣）‎ ‎∴当θ﹣＝，‎ 即θ＝时，四边形OACB的面积最大，其最大面积为．‎