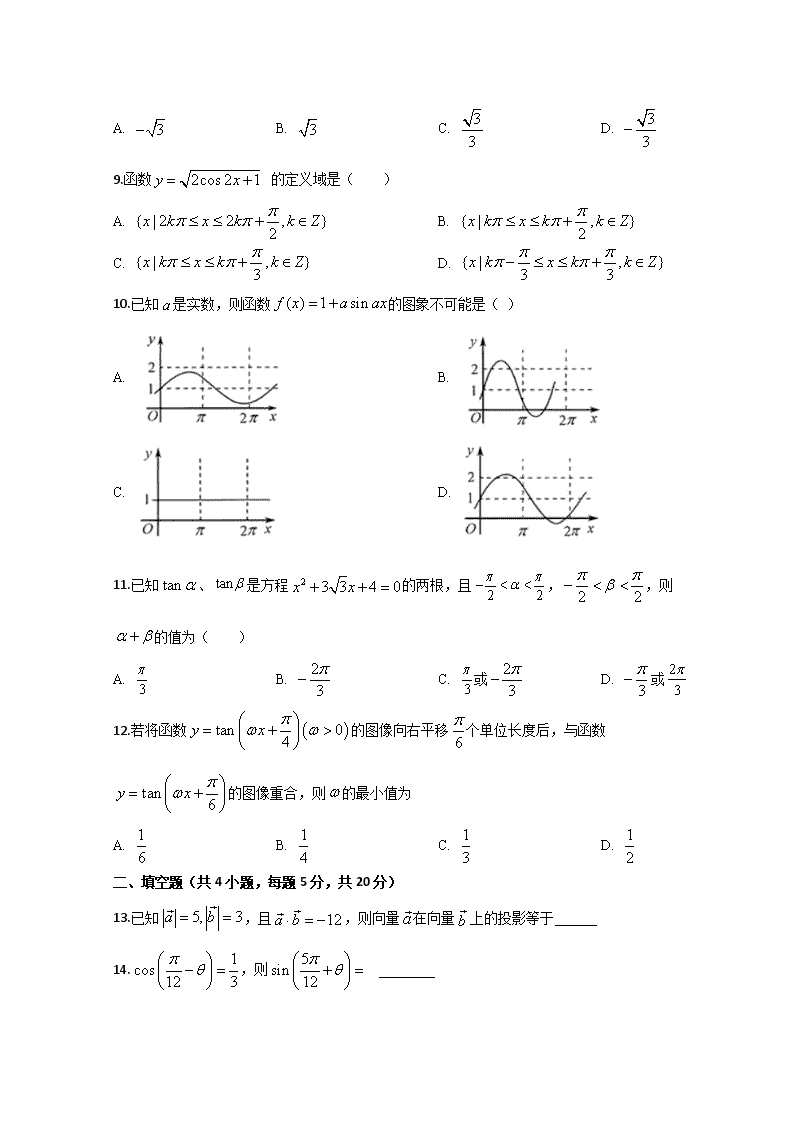- 1.19 MB
- 2021-06-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
绝密★启用前
线上教学检测试卷高一数学试卷
考试范围:必修三;考试时间:120分钟;分值:150分:命题人:
学校: 姓名: 班级: 考号:
注意事项:
1. 答题前填写好自己的姓名、班级、考号等信息
2. 请将答案正确填写在自己的答题纸上
一、选择题(共12小题,每题5分,共60分)
1.179°是()
A. 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
2.已知 且,则角的终边所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.已知向量,,若,则m=( )
A. -1 B. 1 C. 2 D. -2
4.若角的终边与单位圆交于点,则( )
A. B. C. D. 不存在
5.下列函数中,最小正周期为π的是( )
A. B.
C. D.
6.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )
A. 2 B. C. D.
7.已知,则( )
A. B. C. D.
8.( )
A. B. C. D.
9.函数 的定义域是( )
A. B.
C. D.
10.已知a是实数,则函数的图象不可能是( )
A. B.
C. D.
11.已知、是方程的两根,且,,则的值为( )
A. B. C. 或 D. 或
12.若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为
A. B. C. D.
二、填空题(共4小题,每题5分,共20分)
13.已知,且,则向量在向量上的投影等于______
14.,则 ________
15._____
16.已知函数的最小正周期为π,若将该函数的图像向左平移个单位后,所得图像关于原点对称,则m的最小值为________.
三、解答题(共6道解答题,满分70分)
17.(本题满分10分)
(1)已知,且为第三象限角,求,的值
(2)已知,求 的值.
18.(本题满分12分)
设向量,满足,且.
(1)求与的夹角;
(2)求的大小.
19.(本题满分12分)
已知,,.
(1)求;
(2)求.
20.(本题满分12分)
函数的部分图象如图所示.
(1)求的解析式.
(2)若不等式,对任意恒成立,求实数m的取值范围.
21.(本题满分12分)
已知函数,.
(1)求的最大值和最小值;
(2)若关于x的方程在上有两个不同的实根,求实数m的取值范围.
22.(本题满分12分)
已知O为坐标原点,, ,,
若.
⑴ 求函数的最小正周期和单调递增区间;
⑵ 将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求函数在上的最小值.
网课质量检测高一数学试卷
试卷参考答案
一选择题(共12小题,每题5分,共60分)
1.B2.B3.B4.B5.D6.C7.A8.D9.D10.D11.B12.D
二、填空题(共4小题,每题5分,满分20分)
13.-4
14.
15.1
16.
三、解答题
17.(本小题满分10分)
(1);(2)
解析:
(1) 且 为第三象限
…………5分
(2) ……………10分
18.(本小题满分12分)
(1)(2)
解:(1)设与的夹角为.由已知得,即,因此,于是,故,即与的夹角为.…………6分
(2)
.…………12分
19. (本小题满分12分)
(1);(2).
【详解】(1),,…………2分
,…………4分
因此,;…………6分
(2),则,且,,
,…………8分
因此,.…………12分
20. (本小题满分12分)
答案及解析:
(1)f (x)=2sin(2x-).
(2)(-3,2).
【详解】(1)因为,所以,…………3分
又因为,且,所以,
故.…………6分
(2)由(1)知,当时,,
,即,…………9分
又对任意,恒成立,…………10分
,即,
故的取值范围是.…………12分
19. (本小题满分12分)
(1)最大值为3,最小值为2;(2).
【详解】(1),…………4分
,,,…………5分
因此,函数在区间上的最大值为,最小值为
;…………6分
(2)由,即,得.
令,则直线与函数在区间上的图象有两个交点,……9分
如下图所示:
由图象可知,当时,即当时,直线与函数在区间上的图象有两个交点.
因此,实数的取值范围是.…………12分
22.(本小题满分12分)
(1)由题意,,
所以,----------------3分
∴的最小正周期为, ---------------------------------4分
令,得,
所以的单调递增区间为. --------------------------------------------6分
(2)由(1)得,
所以将函数的图象上各点的横坐标伸长为原来的倍(纵坐标不变),
得到函数;---------------------------------------------------------------------------7分
再将得到的图象向左平移个单位,
得到, -----------------------------------------8分
,,
当即时,,----------------------10分
即函数在上的最小值为2. ---------------------12分