2019学年高一数学下学期期中试题新 人教 8页

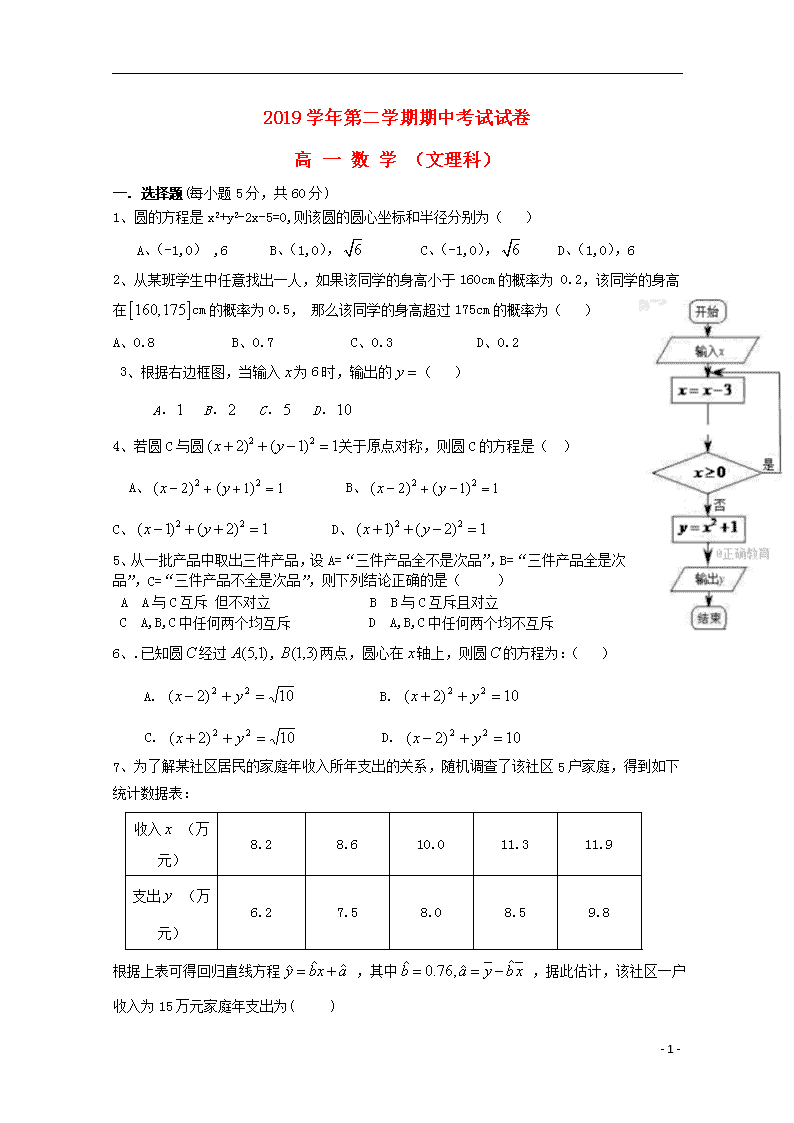
‎2019学年第二学期期中考试试卷 高 一 数 学 （文理科）‎ 一. 选择题(每小题5分，共60分)‎ ‎1、圆的方程是x2+y2-2x-5=0,则该圆的圆心坐标和半径分别为（ ）‎ A、（-1,0） ,6 B、（1,0）， C、（-1,0）， D、（1,0），6‎ ‎2、从某班学生中任意找出一人，如果该同学的身高小于160cm的概率为 0.2，该同学的身高在cm的概率为0.5， 那么该同学的身高超过175cm的概率为（ ）‎ A、0.8 B、0.7 C、0.3 D、0.2‎ ‎ 3、根据右边框图，当输入为6时，输出的（ ）‎ A． B． C． D．‎ ‎4、若圆C与圆关于原点对称，则圆C的方程是（ ）‎ A、 B、‎ C、 D、‎ ‎5、从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品不全是次品”，则下列结论正确的是（ ）‎ A A与C互斥 但不对立 B B与C互斥且对立 ‎ ‎ C A,B,C中任何两个均互斥 D A,B,C中任何两个均不互斥 ‎6、.已知圆经过,两点，圆心在轴上，则圆的方程为：（ ）‎ ‎ A. B. ‎ C. D. ‎ ‎7、为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：‎ 收入 （万元）‎ ‎8.2‎ ‎8.6‎ ‎10.0‎ ‎11.3‎ ‎11.9‎ 支出 （万元）‎ ‎6.2‎ ‎7.5‎ ‎8.0‎ ‎8.5‎ ‎9.8‎ 根据上表可得回归直线方程 ，其中 ，据此估计，该社区一户收入为15万元家庭年支出为( )‎ - 8 -‎ A．11.4万元 B．11.8万元 C．12.0万元 D．12.2万元 ‎8、在某次测量中得到的A样本数据如下：82,84,84,86,86,86,88,‎ ‎88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据，‎ 则A，B两样本的下列数字特征对应相同的是(　　)‎ A．众数 B．平均数 C．中位数 D．标准差 ‎9、给出如图程序框图，其功能是(　　)‎ A．求a－b的值 ‎ B．求b－a的值 C．求|a－b|的值 D．以上都不对 ‎10、为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一个花坛中的概率是（ ）‎ ‎（A） （B） （C） （D）‎ ‎11、 圆的圆心到直线的距离为1，则a＝（ ）‎ ‎（A）− （B）− （C） （D）—‎ ‎12、从区间随机抽取2n个数,，…，，，，…，，构成n个数对，，…，，其中两数的平方和小于1的数对共有m个，则用随机模拟的方法得到的圆周率 的近似值为（ ）‎ ‎（A） （B） （C） （D）‎ ‎ 二. 填空题(每小题5分，共20分)‎ ‎13、．如图甲乙两组数据的茎叶图，那么甲数据的中位数为________，乙数据的中位数为________。‎ ‎14、已知点A（6,0,1），点B（3,5,7），则=________。‎ ‎15、转化为十进制为 ，转化为二进制为 ；‎ ‎16、设直线与圆相交于两点，若，则圆的面积为 。‎ 三. 解答题(共70分) ‎ ‎17、（10分）已知直线l:x–2y–5=0与圆C:相交于A、B两点。求：‎ - 8 -‎ ‎（1）交点A、B的坐标；‎ ‎（2）⊿AOB的面积。‎ ‎18、(12分) 某工厂36名工人的年龄数据如下表。‎ 工人编号 年龄 工人编号 年龄 工人编号 年龄 工人编号 年龄 A. ‎ 40‎ B. ‎ 44‎ C. ‎ 40‎ D. ‎ 41‎ E. ‎ 33‎ F. ‎ 40‎ G. ‎ 45‎ H. ‎ 42‎ I. ‎ 43‎ J. ‎ 36‎ K. ‎ 31‎ L. ‎ 38‎ M. ‎ 39‎ N. ‎ 43‎ O. ‎ 45‎ P. ‎ 39‎ Q. ‎ 38‎ R. ‎ 36‎ S. ‎ 27‎ T. ‎ 43‎ U. ‎ 41‎ V. ‎ 37‎ W. ‎ 34‎ X. ‎ 42‎ Y. ‎ 37‎ Z. ‎ 44‎ AA. ‎ 42‎ BB. ‎ 34‎ CC. ‎ 39‎ DD. ‎ 43‎ EE. ‎ 38‎ FF. ‎ 42‎ GG. ‎ 53‎ HH. ‎ 37‎ II. ‎ 49‎ JJ. ‎ 39‎ ‎（1）用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；‎ ‎（2）计算（1）中样本的平均值和方差；‎ ‎（3）36名工人中年龄在与之间有多少人？所占的百分比是多少（精确到0.01％）？‎ ‎19、（12分）广场舞是现代城市群众文化、娱乐发展的产物，也是城市精神文明建设成果的一个重要象征．2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查，随机抽取了名广场舞者进行调查，将他们年龄分成6段：，，，，，后得到如图所示的频率分布直方图．‎ ‎（1）计算这40名广场舞者中年龄分布在的人数；‎ ‎（2）估计这40名广场舞者年龄的众数和中位数；‎ ‎（3）若从年龄在中的广场舞者中任取2名，求这两名广场舞者中恰有一人年龄在的概率．‎ ‎20、（12分）已知线段AB的两个端点A,B分别在x轴和y轴上滑动，且。‎ ‎（1）求线段AB的中点P的轨迹C的方程；‎ ‎（2）求过点M(1，2)且和轨迹C相切的直线方程。‎ ‎21、（12）某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：‎ - 8 -‎ 年份 ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均纯收入y ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎(1)求y关于t的线性回归方程；‎ ‎(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．‎ 附：回归直线的斜率和截距的最小二乘估计公式分别为：‎ ‎22（12分）已知点P(2,2)，圆C：x2＋y2－8y＝0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点．‎ ‎(1)求M的轨迹方程；‎ ‎(2)当|OP|＝|OM|时，求l的方程及△POM的面积．‎ - 8 -‎ 试卷类型 答案 满分 部分分 A B ‎5‎ ‎0‎ A C ‎5‎ ‎0‎ A D ‎5‎ ‎0‎ A A ‎5‎ ‎0‎ A B ‎5‎ ‎0‎ A D ‎5‎ ‎0‎ A B ‎5‎ ‎0‎ A D ‎5‎ ‎0‎ A C ‎5‎ ‎0‎ A C ‎5‎ ‎0‎ A A ‎5‎ ‎0‎ A C ‎5‎ ‎0‎ 数学客观题答案 - 8 -‎ 主观题答案 ‎13、27 28.5‎ ‎14、‎ ‎15、119 1110111‎ ‎16、‎ ‎17、(10)解：（1）解方程组 得 所以，直线x–2y–5=0与圆C:的交点是A（-5，-5），B（7,1）‎ ‎（2）过圆心O作直线的垂线，垂足为D，则圆心O到直线的距离 在直角三角形AOD中，‎ 所以 ‎⊿AOB的面积 ‎18‎ - 8 -‎ ‎19、解： （1）由表中数据知，这40名广场舞者中年龄分布在的人数为 ‎ 4分 ‎(2)由直方可知这组数据的众数为 6分 因为故位数为 8分 ‎ （3）由直方图可知，年龄在有2人，分别记为，在有4人，分别记为，现从这6人中任选两人，共有如下15种选法：‎ ‎ ‎ ‎ 其中恰有1人在有8种，故其概率为 12分 ‎20、（1）设线段AB的中点P的坐标为（x，y），因为线段AB的两个端点A,B分别在x轴和y轴上，所以点A的坐标为（2x，0），点B的坐标为（0，2y），又因为，则有，= 即 所以线段AB的中点P的轨迹C方程为 …………6分 ‎（2）由（1）知：轨迹C的方程为 ‎1）当过点M直线的斜率存在时，‎ 设其方程为，即 ‎，解得，即直线方程为：‎ ‎2）当过点M直线的斜率不存在时，‎ 其方程为：符合题意 综上所述，过点M且和轨迹C相切的直线方程为：或 ‎…………12分 ‎21、‎ ‎22、　(1)圆C的方程可化为x2＋(y－4)2＝16，所以圆心为C(0,4)，半径为4.‎ - 8 -‎ 设M(x，y)，则由题设知，故（x≠0,x≠2）即(x－1)2＋(y－3)2＝2.‎ 由于点P在圆C的内部，所以M的轨迹方程是(x－1)2＋(y－3)2＝2.‎ ‎(2)由(1)可知M的轨迹是以点N(1,3)为圆心，为半径的圆．‎ 由于|OP|＝|OM|，故O在线段PM的垂直平分线上．‎ 又P在圆N上，从而ON⊥PM.‎ 因为ON的斜率为3，所以l的斜率为－.‎ 故l的方程为y＝－x＋.‎ 又|OM|＝|OP|＝2，O到l的距离为，|PM|＝，所以△POM的面积为.‎ - 8 -‎