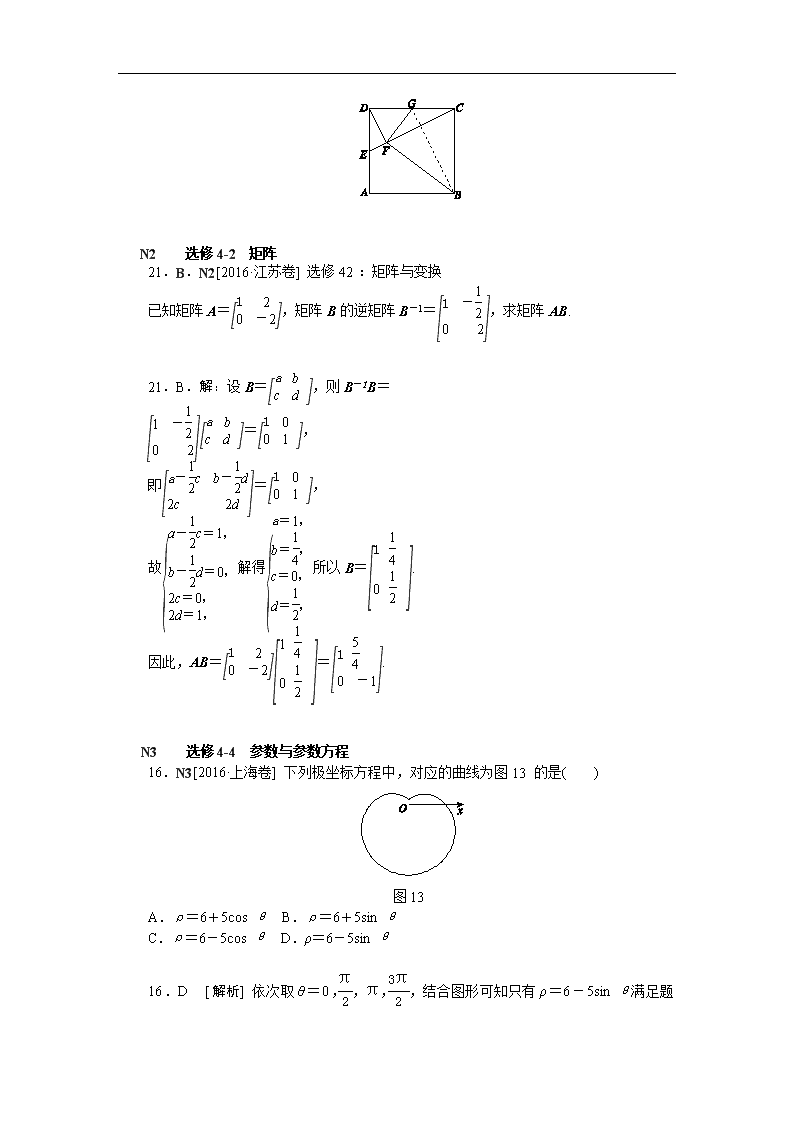2016年高考数学（理科）真题分类汇编N单元 选修4系列 7页

数 学 N单元 选修4系列 ‎ N1 选修4-1 几何证明选讲 ‎21．A.N1[2016·江苏卷] 选修41：几何证明选讲 如图17，在△ABC中，∠ABC＝90°，BD⊥AC，D为垂足，E是BC的中点，求证：∠EDC＝∠ABD.‎ 图17‎ ‎21．A.证明：在△ADB和△ABC中，‎ 因为∠ABC＝90°，BD⊥AC，∠A为公共角，‎ 所以△ADB∽△ABC，于是∠ABD＝∠C.‎ 在Rt△BDC中，因为E是BC的中点，‎ 所以ED＝EC，从而∠EDC＝∠C，‎ 所以∠EDC＝∠ABD.‎ ‎22．N1[2016·全国卷Ⅰ] 选修41：几何证明选讲 如图16所示，△OAB是等腰三角形，∠AOB＝120°.以O为圆心，OA为半径作圆．‎ ‎(1)证明：直线AB与⊙O相切；‎ ‎(2)点C，D在⊙O上，且A，B，C，D四点共圆，证明：AB∥CD.‎ 图16‎ ‎22．证明：(1)设E是AB的中点，连接OE.‎ 因为OA＝OB，∠AOB＝120°，‎ 所以OE⊥AB，∠AOE＝60°.‎ 在Rt△AOE中，OE＝AO，即O到直线AB的距离等于⊙O的半径，所以直线AB与⊙O相切．‎ ‎(2)因为OA＝2OD，所以O不是A，B，C，D四点所在圆的圆心．设O′是A，B，C，D四点所在圆的圆心，作直线OO′.‎ 由已知得O在线段AB的垂直平分线上，又O′在线段AB的垂直平分线上，所以OO′⊥AB.‎ 同理可证，OO′⊥CD，所以AB∥CD.‎ ‎22．N1[2016·全国卷Ⅲ] 选修41：几何证明选讲 如图16，⊙O中AB的中点为P，弦PC，PD分别交AB于E，F两点．‎ ‎(1)若∠PFB＝2∠PCD，求∠PCD的大小；‎ ‎(2)若EC的垂直平分线与FD的垂直平分线交于点G，证明：OG⊥CD.‎ 图16‎ ‎22．解：(1)连接PB，BC，则∠BFD＝∠PBA＋∠BPD，∠PCD＝∠PCB＋∠BCD.‎ 因为AP＝BP，所以∠PBA＝∠PCB，又∠BPD＝∠BCD，所以∠BFD＝∠PCD.‎ 又∠PFB＋∠BFD＝180°，∠PFB＝2∠PCD，所以3∠PCD＝180°，因此∠PCD＝60°.‎ ‎(2)证明：因为∠PCD＝∠BFD，所以∠PCD＋∠EFD＝180°，由此知C，D，F，E四点共圆，其圆心既在CE的垂直平分线上，又在DF的垂直平分线上，故G就是过C，D，F，E四点的圆的圆心，所以G在CD的垂直平分线上，又O也在CD的垂直平分线上，因此OG⊥CD.‎ ‎22．N1[2016·全国卷Ⅱ] 选修41：几何证明选讲 如图15，在正方形ABCD中，E，G分别在边DA，DC上(不与端点重合)，且DE＝DG，过D点作DF⊥CE，垂足为F.‎ ‎(1)证明：B，C，G，F四点共圆；‎ ‎(2)若AB＝1，E为DA的中点，求四边形BCGF的面积．‎ 图15‎ ‎22．解：(1)证明：因为DF⊥EC，所以△DEF∽△CDF，则有∠GDF＝∠DEF＝∠FCB，‎ ＝＝，‎ 所以△DGF∽△CBF，由此可得∠DGF＝∠CBF，‎ 因此∠CGF＋∠CBF＝180°，所以B，C，G，F四点共圆．‎ ‎(2)由B，C，G，F四点共圆，CG⊥CB知FG⊥FB，连接GB.‎ 由G为Rt△DFC斜边CD的中点，知GF＝GC，故Rt△BCG≌Rt△BFG ‎，因此，四边形BCGF的面积S是△GCB面积S△GCB的2倍，即S＝2S△GCB＝2×××1＝.‎ N2 选修4-2 矩阵 ‎21．B．N2[2016·江苏卷] 选修42：矩阵与变换 已知矩阵A＝，矩阵B的逆矩阵B－1＝，求矩阵AB.‎ ‎21．B．解：设B＝，则B－1B＝‎ ＝，‎ 即＝，‎ 故解得所以B＝.‎ 因此，AB＝＝.‎ N3 选修4-4 参数与参数方程 ‎16．N3[2016·上海卷] 下列极坐标方程中，对应的曲线为图13的是(　　)‎ 图13‎ A．ρ＝6＋5cos θ B．ρ＝6＋5sin θ C．ρ＝6－5cos θ D．ρ＝6－5sin θ ‎16．D　[解析] 依次取θ＝0，，π，，结合图形可知只有ρ＝6－5sin θ满足题意．‎ ‎11．N3[2016·北京卷] 在极坐标系中，直线ρcos θ－ρsin θ－1＝0与圆ρ＝2cos θ交于A，B两点，则|AB|＝________．‎ ‎11．2　[解析] 将极坐标方程转化为直角坐标方程进行运算．由x＝ρcos θ，y＝ρsin θ，得直线的直角坐标方程为x－y－1＝0，因为ρ＝2cos θ，ρ2(sin2θ＋cos2θ)＝2ρcos θ，所以圆的直角坐标方程为x2＋y2＝2x，即(x－1)2＋y2＝1，圆心(1，0)在直线上，因此AB为圆的直径，所以|AB|＝2.‎ ‎21．C．N3[2016·江苏卷] 选修44：坐标系与参数方程 在平面直角坐标系xOy中，已知直线l的参数方程为(t为参数)，椭圆C的参数方程为(θ为参数)．设直线l与椭圆C相交于A，B两点，求线段AB的长．‎ ‎21．C．解：椭圆C的普通方程为x2＋＝1.‎ 将直线l的参数方程代入x2＋＝1，得1＋t2＋＝1，即7t2＋16t＝0，解得t1＝0，t2＝－.‎ 所以AB＝|t1－t2|＝.‎ ‎23．N3[2016·全国卷Ⅰ] 选修44：坐标系与参数方程 在直角坐标系xOy中，曲线C1的参数方程为(t为参数，a>0)．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝4cos θ.‎ ‎(1)说明C1是哪一种曲线，并将C1的方程化为极坐标方程；‎ ‎(2)直线C3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C1与C2的公共点都在C3上，求a.‎ ‎23．解：(1)消去参数t得到C1的普通方程x2＋(y－1)2＝a2.C1是以(0，1)为圆心，a为半径的圆．‎ 将x＝ρcos θ，y＝ρsin θ代入C1的普通方程中，得到C1的极坐标方程为ρ2－2ρsin θ＋1－a2＝0.‎ ‎(2)曲线C1，C2的公共点的极坐标满足方程组 若ρ≠0，由方程组得16cos2θ－8sin θcos θ＋1－a2＝0，由已知得tan θ＝2，可得16cos2θ－8sin θcos θ＝0，从而1－a2＝0，解得a＝－1(舍去)或a＝1.‎ 当a＝1时，极点也为C1，C2的公共点，在C3上，‎ 所以a＝1.‎ ‎23．N3[2016·全国卷Ⅲ] 选修44：坐标系与参数方程 在直角坐标系xOy中，曲线C1的参数方程为(α为参数)．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρsinθ＋＝2.‎ ‎(1)写出C1的普通方程和C2的直角坐标方程；‎ ‎(2)设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P的直角坐标．‎ ‎23．解：(1)C1的普通方程为＋y2＝1，C2的直角坐标方程为x＋y－4＝0.‎ ‎(2)由题意，可设点P的直角坐标为(cos α，sin α)．因为C2是直线，所以|PQ|的最小值即为P到C2的距离d(α)的最小值，d(α)＝＝，‎ 当且仅当α＝2kπ＋(k∈Z)时，d(α)取得最小值，最小值为，此时P的直角坐标为(，).‎ ‎23．N3[2016·全国卷Ⅱ] 选修44：坐标系与参数方程 在直角坐标系xOy中，圆C的方程为(x＋6)2＋y2＝25.‎ ‎(1)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；‎ ‎(2)直线l的参数方程是(t为参数)，l与C交于A，B两点，|AB|＝，求l的斜率．‎ ‎23．解：(1)由x＝ρcos θ，y＝ρsin θ可得圆C的极坐标方程为ρ2＋12ρcos θ＋11＝0.‎ ‎(2)在(1)中建立的极坐标系中，直线l的极坐标方程为θ＝α(ρ∈R)．‎ 设A，B所对应的极径分别为ρ1，ρ2，将l的极坐标方程代入圆C的极坐标方程得ρ2＋12ρcos α＋11＝0，‎ 于是ρ1＋ρ2＝－12cos α，ρ1ρ2＝11，‎ 所以|AB|＝|ρ1－ρ2|＝＝.‎ 由|AB|＝得cos2α＝，则tan α＝±，‎ 所以l的斜率为或－.‎ N4 选修4-5 不等式选讲 ‎21．D．N4[2016·江苏卷] 选修45：不等式选讲 设a>0，|x－1|<，|y－2|<，求证：|2x＋y－4|1的解集．‎ 图17‎ ‎24．解：(1)f(x)＝ 则y＝f(x)的图像如图所示．‎ ‎(2)由f(x)的表达式及图像得，当f(x)＝1时，x＝1或x＝3；‎ 当f(x)＝－1时，x＝或x＝5.‎ 故f(x)>1的解集为{x|11的解集为{x或15}.‎ ‎24．N4[2016·全国卷Ⅲ] 选修45：不等式选讲 已知函数f(x)＝|2x－a|＋a.‎ ‎(1)当a＝2时，求不等式f(x)≤6的解集；‎ ‎(2)设函数g(x)＝|2x－1|，当x∈R时，f(x)＋g(x)≥3，求a的取值范围．‎ ‎24．解：(1)当a＝2时，f(x)＝|2x－2|＋2.‎ 解不等式|2x－2|＋2≤6，得－1≤x≤3.‎ 因此f(x)≤6的解集为{x|－1≤x≤3}．‎ ‎(2)当x∈R时，f(x)＋g(x)＝|2x－a|＋a＋|1－2x|≥|2x－a＋1－2x|＋a＝|1－a|＋a，‎ 当x＝时等号成立，‎ 所以当x∈R时，f(x)＋g(x)≥3等价于|1－a|＋a≥3.①‎ 当a≤1时，①等价于1－a＋a≥3，无解．‎ 当a>1时，①等价于a－1＋a≥3，解得a≥2.‎ 所以a的取值范围是[2，＋∞)．‎ ‎24．N4[2016·全国卷Ⅱ] 选修45：不等式选讲 已知函数f(x)＝＋，M为不等式f(x)<2的解集．‎ ‎(1)求M；‎ ‎(2)证明：当a，b∈M时，|a＋b|<|1＋ab|.‎ ‎24．解：(1)f(x)＝ 当x≤－时，由f(x)＜2得－2x＜2，解得x＞－1；‎ 当－＜x＜时，f(x)＜2；‎ 当x≥时，由f(x)＜2得2x＜2，解得x＜1.‎ 所以f(x)＜2的解集M＝{x|－1＜x＜1}．‎ ‎(2)证明：由(1)知，当a，b∈M时，－1＜a＜1，－1＜b＜1，从而(a＋b)2－(1＋ab)2＝a2＋b2－a2b2－1＝(a2－1)(1－b2)＜0，‎ 因此|a＋b|＜|1＋ab|.‎ N5 选修4-7 优选法与试验设计