- 151.16 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019年高考理科数学考前30天--填空题专训(一)
题组一
填空题:本大题共4小题,每小题5分.
1.等比数列各项均为正数,,则 __________.
【答案】20
【解析】由,得,所以 .
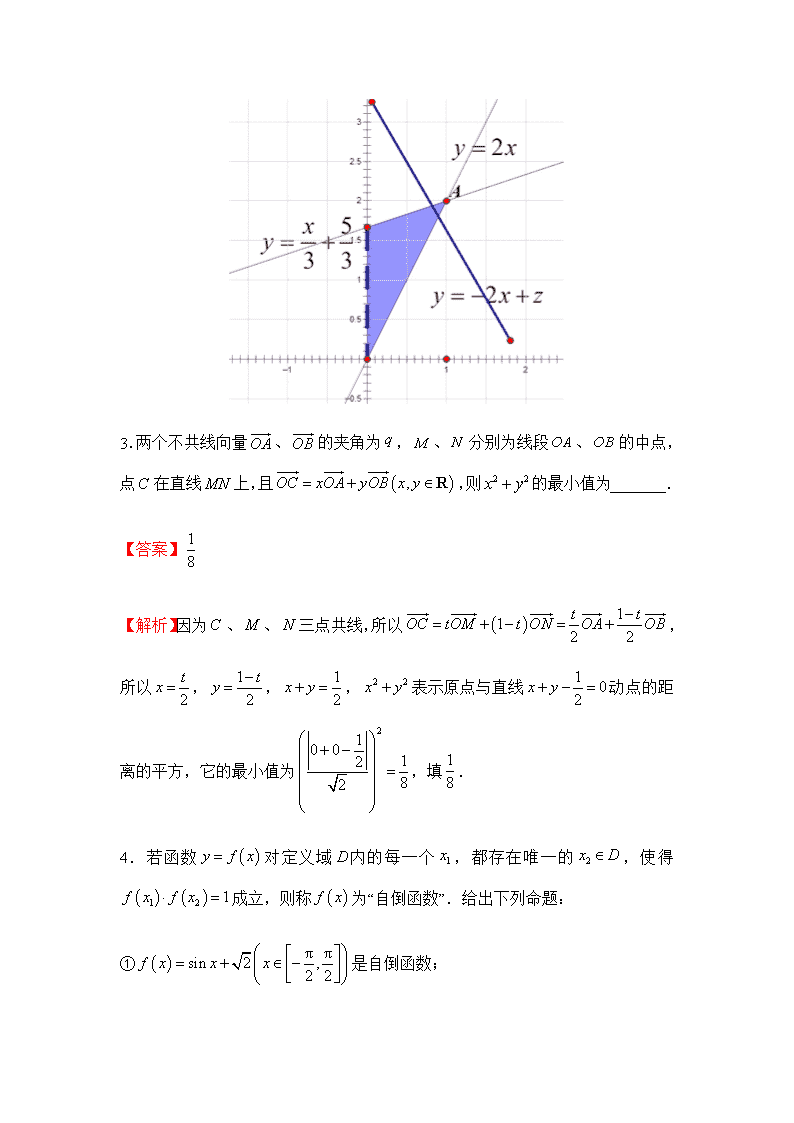
2.已知实数、满足,则的最大值为_______.
【答案】4
【解析】可行域如图所示,当动直线过点时,有最大值,又由得,故的最大值为4.故填4.
3.两个不共线向量、的夹角为,、分别为线段、的中点,点在直线上,且,则的最小值为_______.
【答案】
【解析】因为、、三点共线,所以,所以,,,表示原点与直线动点的距离的平方,它的最小值为,填.
4.若函数对定义域内的每一个,都存在唯一的,使得成立,则称为“自倒函数”.给出下列命题:
①是自倒函数;
②自倒函数可以是奇函数;
③自倒函数的值域可以是;
④若,都是自倒函数,且定义域相同,则也是自倒函数.
则以上命题正确的是________(写出所有正确命题的序号).
【答案】①②
【解析】为上的单调函数,否则方程不止一个实数解.对于①,在是单调增函数,且其值域为,对于任意的,则,故在有唯一解,①正确;对于②,取,,的值域为,因为在和都是单调减函数,故对于,有唯一解,,为“自倒函数”,②正确;对于③,如果的值域为,取,无解,③不正确;④取,,其中,它们都是“自倒函数”,但是,这是常数函数,它不是“自倒函数”.
题组二
1.在中,若,则 .
【解析】由正弦定理得,∴可设,,,
∴.
【答案】
2.若,则 .
【解析】∵,∴,,
∴,,∴.
【答案】593
3.若的展开式中的系数为20,则 .
【解析】∵的展开式中的系数为,∴.
【答案】
4.已知一个四面体的每个顶点都在表面积为的球的表面上,且,,则 .
【解析】由题可知四面体的对棱都相等,故该四面体可以通过补形补成一个长方体,如图所示,设,,,则,,∴,∴.
【答案】
相关文档
- 辽宁省大连市2020届高三第二次模拟2021-06-1624页
- 2017-2018学年湖北省沙市中学高二2021-06-169页
- 2017-2018学年湖北省长阳一中高二32021-06-168页
- 2013年普通高等学校招生全国统一考2021-06-169页
- 2018-2019学年河南省高二上学期期2021-06-1614页
- 2018-2019学年安徽省郎溪中学高一2021-06-169页
- 西藏自治区日喀则市南木林高级中学2021-06-1617页
- 2019-2020学年湖南省衡阳市第八中2021-06-1615页
- 广东省揭阳市2020届高三下学期线上2021-06-165页
- 2019-2020学年浙江省杭州市西湖高2021-06-1626页