新教材数学人教B版必修第二册教师用书（含习题测试）：6-2-1　向量的加法运算 13页

6.2 平面向量的运算 6.2.1 向量的加法运算 课 标 解 读 课标要求 核心素养 1.借助实例理解并掌握向量加法的概念. 2.掌握向量加法运算法则,并能熟练地进行 加法运算.(重点) 3.理解向量加法运算的几何意义.(难点) 1.通过向量加法的三角形法则、平行四边形法 则,培养直观想象核心素养. 2.借助向量加法的运算律进行相关运算,培养数 学运算核心素养. 俄罗斯著名寓言作家克雷洛夫在他所著的《克雷洛夫寓言》中有一篇《天鹅、 梭子鱼和虾》的故事,故事的大意是这样的:有一天,天鹅、梭子鱼和虾一起拉一车 货物,天鹅想,我的家在天上,应该把货物拉到我家,于是,天鹅伸长脖子拼命往天 上飞.梭子鱼想,我的家在河里,应该往河里拉,于是,梭子鱼使劲往河里拽.虾想, 我的家在池塘里,应该把货送到池塘,于是,虾弓着身子往池塘拉.他们三个累的精 疲力尽,车子却纹丝不动. 问题 1:车子为什么纹丝不动? 答案 天鹅、梭子鱼和虾用力的方向不一致. 问题 2:这则故事给我们的启示是什么? 答案 要想成功,就要好好合作,用力方向要合理. 1.向量的加法 (1)定义:求①两个向量和的运算,叫做向量的加法.这种求向量和的方法,称 为向量加法的三角形法则. 对于零向量与任意向量 a,规定 0+a=a+0=a. (2)向量求和的法则: 三角 形法 则 已知非零向量 a,b,在平面内任取一点 A,作 ′ =a, ′ =b,则向量 叫做 a 与 b 的和,记作 ②a+b,即 a+b= ′ + ′ = 平行 四边 形法 则 以同一点 O 为起点的两个已知向量 a,b,以 OA,OB 为邻边作③▱OACB,则以 O 为起点的向 量 (OC 是▱OACB 的对角线)就是向量 a 与 b 的和,即 =a+b 特别提醒 三角形法则与平行四边形法则的区别与联系 三角形法则 平行四边形法则 区别 满足条 件 两向量“首尾 相接” 两向量“共起点” 适用范 围 所有向量 不共线的两向量 联系 平行四边形法则与三角形法则在本质上是一致的.这两种求向量和的方法,通过向量平移能 相互转化,解决具体问题时视情况而定 2.向量加法的运算律 (1)交换律:a+b=④b+a. (2)结合律:(a+b)+c=⑤a+(b+c). 思考:向量加法的运算律与实数加法的运算律相同吗? 提示 相同. 3.|a|-|b|,|a±b|,|a|+|b|三者的关系 根据三角形的三边关系可得|a|-|b|≤|a+b|≤|a|+|b|,当且仅当向量 a,b 方向 相同时取“=”. 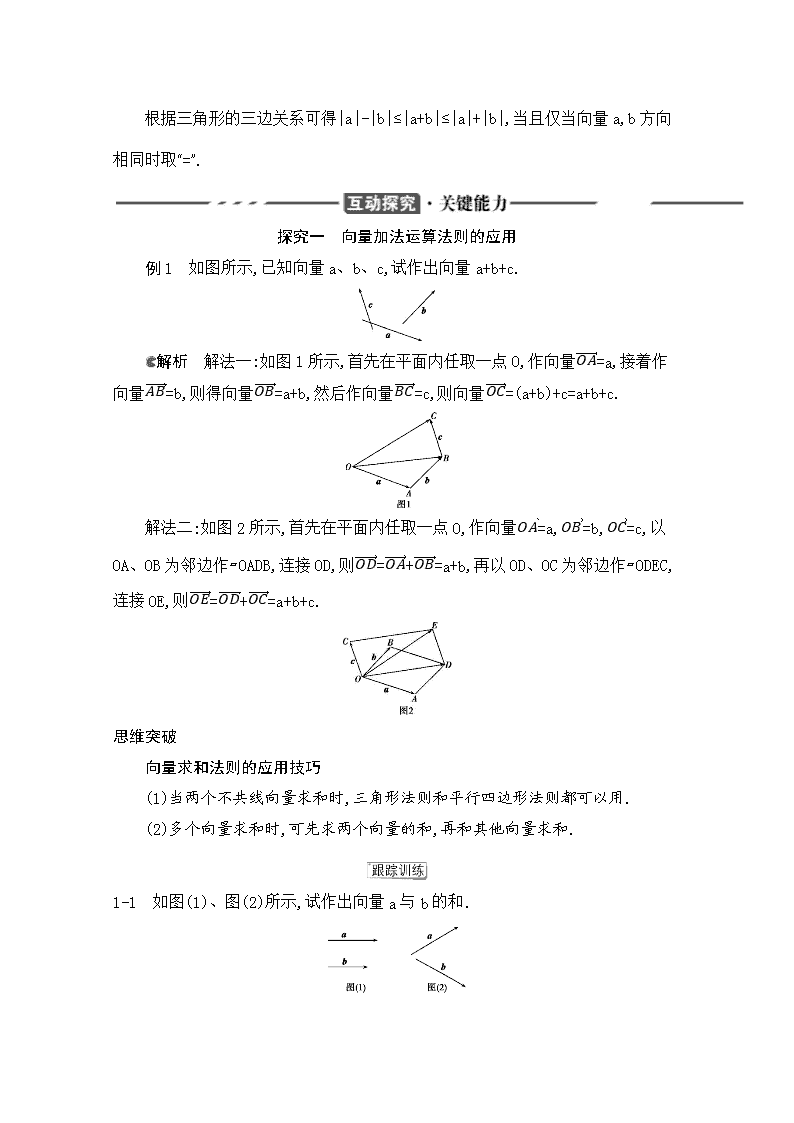探究一 向量加法运算法则的应用 例 1 如图所示,已知向量 a、b、c,试作出向量 a+b+c. 解析 解法一:如图 1 所示,首先在平面内任取一点 O,作向量 =a,接着作向 量 ′ =b,则得向量 ′ =a+b,然后作向量 ′ =c,则向量 =(a+b)+c=a+b+c. 解法二:如图 2 所示,首先在平面内任取一点 O,作向量 =a, ′ =b, =c,以 OA、OB 为邻边作▱OADB,连接 OD,则 = + ′ =a+b,再以 OD、OC 为邻边作▱ODEC, 连接 OE,则 = + =a+b+c. 思维突破 向量求和法则的应用技巧 (1)当两个不共线向量求和时,三角形法则和平行四边形法则都可以用. (2)多个向量求和时,可先求两个向量的和,再和其他向量求和. 1-1 如图(1)、图(2)所示,试作出向量 a 与 b 的和. 解析 如图①、图②所示. ′ 即为所求. 探究二 向量加法运算律的应用 例 2 化简下列各式: (1) ′ + + + ′ + ; (2)( ′ + )+ + ′ + . 解析 (1) ′ + + + ′ + = ′ + ′ + + + = + + + = + =0. (2)( ′ + )+ + ′ + =( ′ + ′ )+( + )+ = + + = + =0. 2-1 化简:( ′ + ′ )+( ′ + ′ )+ = . 答案 解析 ( ′ + ′ )+( ′ + ′ )+ =( ′ + ′ )+ ′ +( ′ + )= + ′ + ′ = . 探究三 向量加法的实际应用 例 3 在某地抗震救灾时,一架飞机先从 A 地按北偏东 35°方向飞行 800km 到 达 B 地接到受伤人员,然后从 B 地按南偏东 55°方向飞行 800km 将受伤人员送往 C 地医院,求这架飞机飞行的路程及两次飞行的位移的和. 解析 如图所示,设 ′ , ′ 分别表示飞机从 A 地按北偏东 35°方向飞行 800km 到达 B 地,从 B 地按南偏东 55°方向飞行 800km 到达 C 地. 则飞机飞行的路程是| ′ |+| ′ |,两次飞行的位移的和是 ′ + ′ = . 依题意,有| ′ |+| ′ |=800+800=1600(km),∠ABC=35°+55°=90°, 所以| |= |′ | 2 + |′ | 2 = 800 2 + 800 2 =800 2 (km). 其中∠BAC=45°,所以方向为北偏东 35°+45°=80°. 故飞机飞行的路程是 1600km,两次飞行的位移和的大小为 800 2 km,方向为北 偏东 80°. 思维突破 向量加法解决实际问题的应用技巧 (1)准确画出几何图形,将几何图形中的边转化为向量. (2)将所求问题转化为向量的加法运算,进而利用向量加法的几何意义进行求 解. 3-1 如图,用两根绳子把重 10N 的物体 W 吊在水平木杆 AB 上,∠ACW=150°,∠BCW=120°,求 A 处和 B 处所受力的大小(绳子的质量忽略不计). 解析 如图,设 , 分别表示 A,B 所受的力, 10N 的重力用 表示,则 + = . 易得∠ECG=180°-150°=30°,∠FCG=180°-120°=60°, ∴| |=| |×cos30° =10× 3 2 =5 3 (N). | |=| |×cos60°=10× 1 2 =5(N). 故 A 处所受的力的大小为 5 3 N,B 处所受的力的大小为 5N. 1.在四边形 ABCD 中,若 = ′ + ,则( ) A.四边形 ABCD 一定是矩形 B.四边形 ABCD 一定是菱形 C.四边形 ABCD 一定是正方形 D.四边形 ABCD 一定是平行四边形 答案 D 由向量加法的平行四边形法则可知,四边形 ABCD 必为平行四边形. 2.化简 + + + 的结果为( ) A. B. C. D. 答案 B + + + = +0= . 3.(多选题)在如图所示的▱ABCD 中,下列结论正确的是( ) A. ′ = B. + ′ = C. ′ = ′ + D. + ′ =0 答案 ABD 由▱ABCD 知 A,B,D 正确,因为 ′ = + ′ ≠ ′ + ,所以 C 错误. 4.若 a 表示“向东走 8km”,b 表示“向北走 8km”,则|a+b|= ,a+b 的方向 是 . 答案 8 2 km;东北方向 解析 如图所示,作 =a, ′ =b, 则 a+b= + ′ = ′ , 所以|a+b|=| ′ |= 8 2 + 8 2 =8 2 (km), 因为∠AOB=45°, 所以 a+b 的方向是东北方向. 5.如图,已知向量 a,b,c,求作向量 a+b+c. 解析 在平面内任取一点 O,作 =a, ′ =b, ′ =c,如图所示: 则由向量加法的三角形法则,得 ′ =a+b, =a+b+c,故 即为所求向量 a+b+c. 逻辑推理——向量加法的应用 如图,在正六边形 OABCDE 中, =a, =b,试用向量 a,b 将 ′ , , 表示出 来. 解析 如图,连接 BE,AD,设正六边形的中心为 P,则四边形 ABPO,AOEP,ABCP,OPDE 均为平行四边形. 由向量加法的平行四边形法则得 = + =a+b. ∵ ′ = = , ∴ ′ = =a+b. 在△AOB 中,根据向量加法的三角形法则, 得 ′ = + ′ =a+a+b. 同理,在△OBC 中, = ′ + ′ =a+a+b+b, 在△OED 中, = + = + =b+a+b. 素养探究:用已知向量表示待求向量,可以利用向量的平移性,根据三角形法 则、平行四边形法则,结合正六边形的几何性质转化求解,体现了逻辑推理的核心 素养. P,Q 是△ABC 的边 BC 上的两点,且 BP=QC.求证: ′ + = + . 证明 如图,取 BC 的中点 O,连接 AO 并延长至点 D,使 OD=AO,连接 BD,CD,则四边 形 ABDC 是平行四边形,所以 ′ + = ,又 BP=QC,BO=CO,所以 PO=QO,连接 PD,QD, 则四边形 APDQ 是平行四边形,所以 + = ,所以 ′ + = + . 1.(多选题)下列等式正确的有( ) A. ′ + ′ =0 B. = + ′ + ′ C. + + + =0 D. ′ + + ′ + =0 答案 ABD 由向量加法的三角形法则和零向量的定义可知 ′ + ′ =0,故 A 正 确. + ′ + ′ = ′ + ′ + = ,故 B 正确. + + + = + + = ,故 C 不正确. ′ + + ′ + = + ′ + ′ + =0,故 D 正确. 2.在▱ABCD 中,若| ′ + ′ |=| ′ + ′ |,则四边形 ABCD 是( ) A.菱形 B.矩形 C.正方形 D.不确定 答案 B 3.在▱ABCD 中,O 是对角线的交点,下列结论正确的是( ) A. ′ = , ′ = B. + = C. + = + D. ′ + ′ + = 答案 C 4.在矩形 ABCD 中,AB= 3 ,BC=1,则向量 ′ + + 的长度为( ) A.2 B.2 3 C.3 D.4 答案 D 在矩形 ABCD 中,AB= 3 ,BC=1, 所以 AC=2, 因为 ′ + + = ′ + ′ + = + =2 ,故其长度为 4. 5.根据图示填空,其中 a= ,b= ,c= ′ ,d= ′ . (1)a+b+c= ; (2)b+d+c= . 答案 (1) ′ (2) 解析 (1)a+b+c= + + ′ = ′ . (2)b+d+c= + ′ + ′ = + ′ + ′ = . 6.若 P 为△ABC 的外心,且 + ′ = ,则∠ACB= . 答案 120° 解析 由 + ′ = 知四边形 ACBP 为平行四边形, 又 P 为外心, 所以四边形 ACBP 为菱形, 且 PA=PC=AC,∠ACP=60°, 易得∠ACB=120°. 7.如图所示,已知在矩形 ABCD 中,| |=4 3 ,设 ′ =a, ′ =b, ′ =c,求|a+b+c|的大 小. 解析 如图所示,过点 D 作 AC 的平行线,交 BC 的延长线于点 E. ∵DE∥AC,AD∥BE, ∴四边形 ADEC 为平行四边形, ∴ = , = , 于是 a+b+c= ′ + ′ + ′ = + ′ = + ′ = ′ = + =2 , ∴|a+b+c|=2| |=8 3 . 8.(多选题)向量 a、b 均为非零向量,下列说法中正确的是( ) A.若向量 a 与 b 反向,且|a|>|b|,则向量 a+b 与 a 的方向相同 B.若向量 a 与 b 反向,且|a|<|b|,则向量 a+b 与 a 的方向相同 C.若向量 a 与 b 同向,则向量 a+b 与 a 的方向相同 D.若向量 a 与 b 同向,则向量 a+b 与 b 的方向相同 答案 ACD 当向量 a 与 b 反向,且|a|<|b|时,向量 a+b 与 b 的方向相同,只有 B 错误,A、C、D 都正确. 9.(多选题)如图,D,E,F 分别是△ABC 的边 AB,BC,CA 的中点,则下列等式中正确的是 ( ) A. + + =0B. + ′ + =0 C. + + = ′ D. + + = ′ 答案 ABC + + = + =0,故 A 正确; + ′ + = + + =0,故 B 正确; + + = + = + ′ = ′ ,故 C 正确; + + = +0= = ′ ≠ ′ ,故 D 错 误. 10.已知▱ABCD,设 ′ + + ′ + =a,且 b 是非零向量,则下列结论:①a∥b;②a+b=a; ③a+b=b;④|a+b|<|a|+|b|,其中正确的有 .(填序号) 答案 ①③ 解析 因为在平行四边形 ABCD 中, ′ + =0, ′ + =0,所以 a 为零向量,因为零 向量和任意向量都平行,零向量和任意向量的和等于这个向量本身,所以①③正确, ②④错误. 11.雨滴在下落一定时间后的运动是匀速的,无风时雨滴下落的速度是 4.0m/s,现 在有风,风使雨滴以 4 3 3 m/s 的速度水平向东移动,求雨滴着地时的速度和方向. 解析 如图,用 表示雨滴下落的速度, ′ 表示风使雨滴水平向东移动的速度. 以 , ′ 为邻边作四边形 OACB, 就是雨滴下落的实际速度. 在 Rt△OAC 中,| |=4,| |= 4 3 3 , ∴| |= | | 2 + | | 2 = 4 2 + 4 3 3 2 = 8 3 3 , ∴tan∠AOC= | | | | = 4 3 3 4 = 3 3 ,∴∠AOC=30°. 故雨滴着地时的速度大小是 8 3 3 m/s,方向为南偏东 30°. 12.过△ABC 内一点 M 任作一条直线 l,再分别过顶点 A,B,C 作 l 的垂线,垂足分别为 D,E,F,若 + ′ + =0 恒成立,则点 M 是△ABC 的( ) A.垂心 B.重心 C.外心 D.内心 答案 B 设直线 l 过点 A,则|AD|=0,有 ′ + =0. 则直线 AM 经过 BC 的中点,同理,直线 BM 经过 AC 的中点.直线 CM 经过 AB 的中点, 所以点 M 是△ABC 的重心. 13.设|a|=2,e 为单位向量,求|a+e|的最大值. 解析 在平面内任取一点 O,作 =a, ′ =e, 则 a+e= + ′ = ′ ,因为 e 为单位向量,所以点 B 在以 A 为圆心的单位圆上(如图所 示), 由图可知,当点 B 在点 B1 处时,O,A,B1 三点共线,此时| ′ |(即|a+e|)最大,最大值是 3.