【数学】四川省眉山市仁寿县文宫中学2019-2020学年高一上学期期中考试试题 （解析版） (1) 11页

www.ks5u.com 四川省眉山市仁寿县第二中学、华兴中学2019-2020学年高一上学期期末模拟数学试题 第Ⅰ卷（选择题，共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有且只有一项是符合题目要求的.‎ ‎1.已知集合，集合，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】，，故.‎ 故选：C.‎ ‎2.函数且的图象必经过点（ ）‎ A. (0，1) B. (2，1)‎ C. (-2，2) D. (2，2)‎ ‎【答案】D ‎【解析】令指数此时,故经过定点.‎ 故选D ‎3.已知函数，则函数定义域为 （ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】由题设有，故，所以函数的定义域为.‎ 故选：A.‎ ‎4.下列函数中，最小正周期为且图象关于原点对称的函数是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】y＝cos（2x）＝﹣sin2x，是奇函数，函数的周期为：π，满足题意，所以A正确 y＝sin（2x）＝cos2x，函数是偶函数，周期为：π，不满足题意，所以B不正确；‎ y＝sin2x+cos2xsin（2x），函数是非奇非偶函数，周期为π，所以C不正确；‎ y＝sinx+cosxsin（x），函数是非奇非偶函数，周期为2π，所以D不正确；‎ 故选A．‎ ‎5.幂函数在上为增函数，则实数的值为( )‎ A. 0 B. 1 C. 2 D. 1或2‎ ‎【答案】C ‎【解析】因为是幂函数，所以可得或，又当时在上为减函数，所以不合题意，时，在上为增函数，合题意，故选C.‎ ‎6.函数的零点所在的大致区间是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】因为,‎ 且,故的零点所在的大致区间是 故选C ‎7.已知，则的大小关系为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】因为为单调增函数且，‎ 所以，故，‎ 又为减函数且，所以即 ，故.‎ 故选：D.‎ ‎8.已知，则（ ）‎ A. B. C. D. 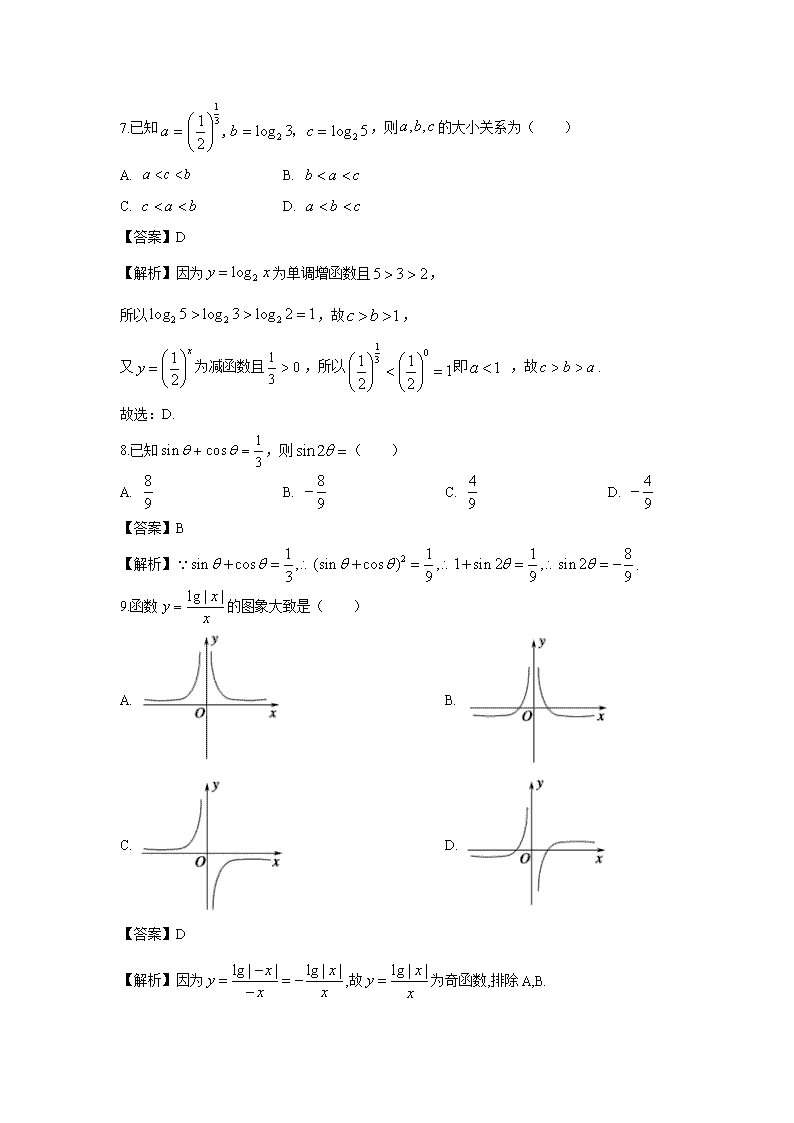‎ ‎【答案】B ‎【解析】.‎ ‎9.函数的图象大致是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】因为,故为奇函数,排除A,B.‎ 又当时,故有零点,排除C.‎ 故选D ‎10.已知函数是定义在R上的偶函数，在区间上递减，且，则不等式的解集为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】因为为偶函数，故.‎ 当时，等价于，‎ 因为在上递减，故在的解为， ‎ 当时，等价于，‎ 因为在上递减且为偶函数，故在上为增函数，‎ 故在的解为，‎ 综上，的解集为.‎ 故选：C.‎ ‎11.已知，则等于( )‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】＝-sin[]＝‎ 故选C．‎ ‎12.已知函数，的部分图象如图所示，下列说法正确的是（ ）‎ A. 的图象关于直线对称 B. 的图象关于点 对称 C. 将函数 的图象向左平移 个单位得到函数的图象 D. 若方程在上有两个不相等的实数根，则m的取值范围是 ‎【答案】D ‎【解析】由函数的图象可得，求得， ‎ 由五点法作图可得，求得，所以，‎ 当时，，不是最值，故A不成立；‎ 当时，，不是函数的对称中心，故B不成立；‎ 将函数的图象向左平移个单位得到函数 的图象，故C不成立；‎ 当时，，‎ 因为，‎ 故方程在上两个不相等的实数根时，则的取值范围是，所以D成立，故选D.‎ 第Ⅱ卷（非选择题，共90分）‎ 二、填空题:本大题共4小题，每小题5分，共20分. 请将答案填在答题卷中的相应位置.‎ ‎13.已知扇形的面积为，圆心角为，则该扇形半径为__________．‎ ‎【答案】2‎ ‎【解析】圆心角为 扇形的面积为 故答案为2‎ ‎14.在区间上单调递减，则a的取值范围是______．‎ ‎【答案】‎ ‎【解析】解：函数的图象是开口朝上，且以直线为对称轴的抛物线， 若在区间上单调递减， 则，解得：，故答案为．‎ ‎15.（1+tan17°）（1+tan28°）=______．‎ ‎【答案】2‎ ‎【解析】原式=1+tan17°+tan28°+tan17°•tan28°，又tan（17°+28°）==tan45°=1，‎ ‎∴tan17°+tan28°=1﹣tan17°•tan28°，‎ 故 （1+tan17°）（1+tan28°）=2，‎ 故答案为 2．‎ ‎16.已知函数若方程恰有4个不同的实根，则实数a的的取值范围为__________．‎ ‎【答案】‎ ‎【解析】作出函数作出函数的图象，根据直线与的图象有4个交点，‎ 所以有．故答案为．‎ 三、解答题：本大题共6小题，共70分. 解答应写出文字说明，证明过程或演算步骤.‎ ‎17.化简或计算下列各题：‎ ‎（Ⅰ）；‎ ‎（Ⅱ）已知，求 解：（Ⅰ）原式 ‎.‎ ‎（Ⅱ），，‎ 故.‎ ‎18.已知集合．‎ ‎（1）求；‎ ‎（2）若，求实数的取值范围．‎ 解：，‎ ‎（1）；‎ ‎（2）∵，∴，‎ ‎∵，∴，∴．‎ ‎19.已知函数的部分图象如图所示．‎ ‎（1）求的解析式；‎ ‎（2）将图象上所有点向左平行移动个单位长度，得到图象，求函数在上的单调递增区间．‎ 解：（1）由图象可知,周期, ‎ ‎∴ ， ‎ ‎∴，‎ 又点在函数的图象上，‎ ‎∴，‎ ‎∴‎ ‎∴，‎ 又，∴，∴ ．‎ ‎(2)由(1)知，‎ 因此.‎ 由，，‎ 又,∴‎ 故函数在上的单调递增区间为．‎ ‎20.已知函数．‎ ‎（Ⅰ）求的最小正周期及对称中心；‎ ‎（Ⅱ）若，求的最大值和最小值．‎ 解：（Ⅰ）‎ ‎∴的最小正周期为，‎ 令，则，‎ ‎∴的对称中心为；‎ ‎（Ⅱ）∵∴∴‎ ‎∴‎ ‎∴当时，的最小值为；‎ 当时，的最大值为．‎ ‎21.近年来，中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁，百般刁难，并不断加大对各国的施压，拉拢他们抵制华为5G，然而这并没有让华为却步.华为在2018年不仅净利润创下记录，海外增长同样强劲.今年，我国华为某一企业为了进一步增加市场竞争力，计划在2020年利用新技术生产某款新手机.通过市场分析，生产此款手机全年需投入固定成本250万，每生产（千部）手机，需另投入成本万元，且 ，由市场调研知，每部手机售价0.7万元，且全年内生产的手机当年能全部销售完.‎ ‎（Ⅰ）求出2020年的利润（万元）关于年产量（千部）的函数关系式，（利润=销售额—成本）；‎ ‎（Ⅱ）2020年产量为多少（千部）时，企业所获利润最大？最大利润是多少？‎ 解：（Ⅰ）当时，；‎ 当时，，‎ ‎ .‎ ‎（Ⅱ）若，，‎ 当时，万元 .‎ 若，，‎ 当且仅当时，即时，万元 .‎ ‎2020年产量为100（千部）时，企业所获利润最大，最大利润是9000万元.‎ ‎22.已知奇函数的定义域为.‎ ‎(1)求实数a，b的值；‎ ‎(2)判断函数的单调性，并用定义证明；‎ ‎(3)若实数m满足，求m的取值范围.‎ 解：（1）是奇函数,,得,‎ 定义域关于原点对称,故.‎ ‎（2）在递增 证明：设,且 则 ‎,又 ‎,即 在递增；‎ ‎（3）由题意可得 等价于,得.‎