【数学】甘肃省白银市会宁县第四中学2019-2020学年高一下学期期中考试试题 （解析版） 12页

甘肃省白银市会宁县第四中学2019-2020学年高一下学期期中考试数学试题 一、选择题（共12小题，注意：将你选的答案填在答题卡上）‎ ‎1.设集合，，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】∵，，‎ ‎∴‎ 故选：C.‎ ‎2.已知两个单元分别存放了变量和，试设计交换这两个变量值的语句正确的是（ ）.‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】，将的值赋值给，‎ ‎，将的值赋值给，此时已经将的值换给，‎ ‎，将的值赋值给，此时已经将的值换给，‎ 选项A，赋值后的值不存在；选项C，赋值后的值不存在；选项D，赋值后的值不存在.‎ 故选：B.‎ ‎3.下列说法正确的是（ ）‎ A. 第二象限角大于第一象限角 B. 不相等的角终边可以相同 C. 若是第二象限角，一定是第四象限角 D. 终边在轴正半轴上的角是零角 ‎【答案】B ‎【解析】A选项，第一象限角，而是第二象限角，∴该选项错误；‎ B选项，与终边相等，但它们不相等，∴该选项正确；‎ C选项，若是第二象限角，则，‎ ‎∴是第三象限角或第四象限角或终边在轴负半轴上的轴线角，∴该选项错误；‎ D选项，角的终边在轴正半轴上，但不是零角，∴该选项错误.‎ 故选：.‎ ‎4.《周易》历来被人们视作儒家群经之首，它表现了古代中华民族对万事万物的深刻而又朴素的认识，是中华人文文化的基础，它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为：把阳爻“”当作数字“‎1”‎，把阴爻“”当作数字“‎0”‎，则八卦所代表的数表示如下：‎ 依此类推，则六十四卦中的“井”卦，符号“”表示的十进制数是（ ）.‎ A. 11 B. ‎18 ‎C. 22 D. 26‎ ‎【答案】C ‎【解析】六十四卦中符号“”表示二进制数的010110，‎ 转化为十进制数的计算为.‎ 故选：C.‎ ‎5.某县共有300个村，现采用系统抽样方法，抽取15个村作为样本，调查农民的生活和生产状况，将300个村编上1到300的号码，求得间隔数，即每20个村抽取一个村，在1到20中随机抽取一个数，如果抽到的是7，则从41到60这20个数中应取的号码数是（ ）‎ A. 45 B. ‎46 ‎C. 47 D. 48‎ ‎【答案】C ‎【解析】根据题意，样本间隔数，‎ 在1到20中抽到的是7，‎ 则41到60为第3组，此时对应的数为7+2×20＝47.‎ 故选：C.‎ ‎6.如果数据的平均数为，方差为，则，，…，的平均数和方差分别为（ ）‎ A. ， B. ， ‎ C. ， D. 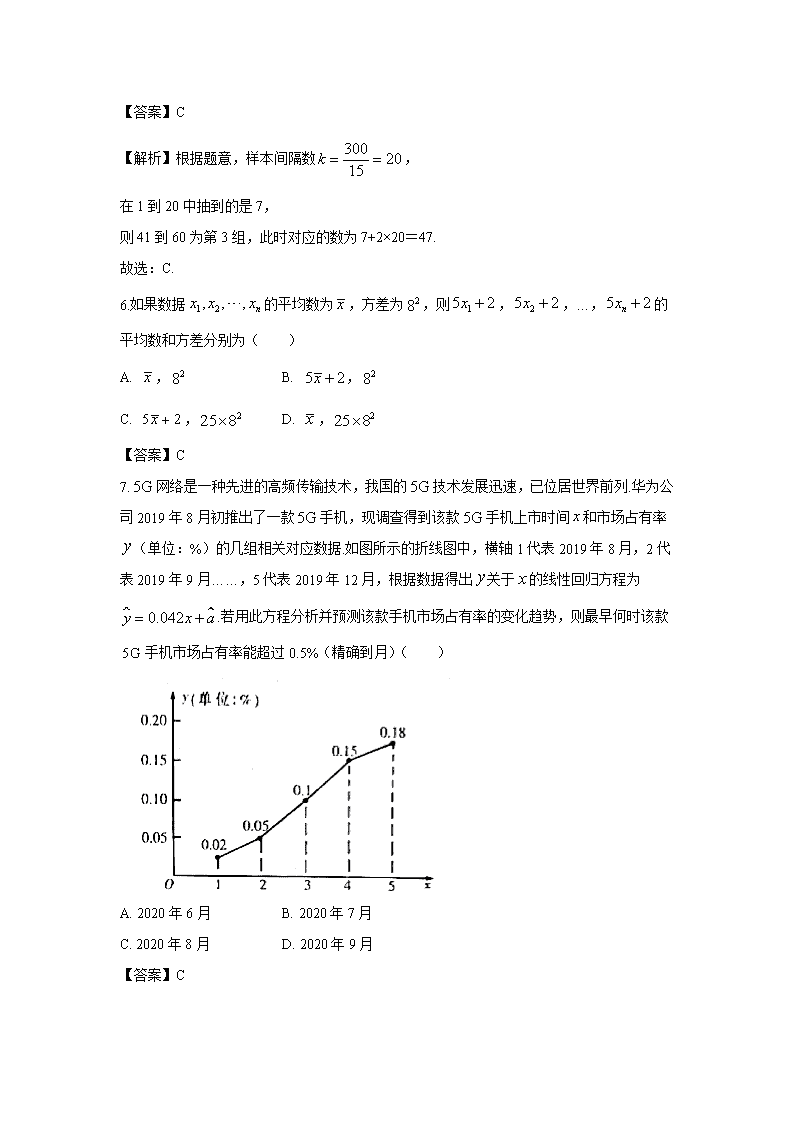，‎ ‎【答案】C ‎7.网络是一种先进的高频传输技术，我国的技术发展迅速，已位居世界前列.华为公司2019年8月初推出了一款手机，现调查得到该款手机上市时间和市场占有率（单位：%）的几组相关对应数据.如图所示的折线图中，横轴1代表2019年8月，2代表2019年9月……，5代表2019年12月，根据数据得出关于的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势，则最早何时该款手机市场占有率能超过0.5%（精确到月）（ ）‎ A. 2020年6月 B. 2020年7月 ‎ C. 2020年8月 D. 2020年9月 ‎【答案】C ‎【解析】，‎ 点在直线上 ‎，‎ 令 因为横轴1代表2019年8月，所以横轴13代表2020年8月，‎ 故选：C ‎8.从5个同类产品（其中3个正品，2个次品）中，任意抽取2个，下列事件发生概率为的是（ ）‎ A. 2个都是正品 B. 恰有1个是正品 ‎ C. 至少有1个正品 D. 至多有1个正品 ‎【答案】C ‎【解析】易得两个都是次品的概率是，故发生概率为的事件是“两个都是次品”的对立事件，即“至少有1个正品”‎ 故选：C.‎ ‎9.已知扇形的圆心角为，面积为，则该扇形的周长为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】，故，周长为：.‎ 故选：A ‎ ‎10.剪纸艺术是最古老的中国民间艺术之一，作为一种镂空艺术，它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术，通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1‎ 的正方形剪纸图案，中间黑色大圆与正方形的内切圆共圆心，圆与圆之间是相切的，且中间黑色大圆的半径是黑色小圆半径的2倍，若在正方形图案上随机取一点，则该点取自白色区域的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由题意，正方形的内切圆的半径为,‎ 设中间黑色的小圆的半径为，则中间黑色的大圆的半径为2.‎ 所以，则，‎ 即中间黑色的大圆的半径为，中间黑色的小圆的半径为.‎ 所以白色的区域的面积为 则该点取自白色区域的概率为 故选：D ‎11.已知角的顶点为坐标原点，始边与轴的非负半轴重合，终边上一点，则（ ）‎ A. B. ‎ C D. ‎ ‎【答案】A ‎【解析】‎ ‎【详解】由三角函数定义得tan，即,得3cos解得或（舍去）‎ 故选A ‎12. 某射手在一次射击中，射中10环，9环，8环的概率分别是0.20，0.30，0.10．则此射手在一次射击中不够8环的概率为（ ）‎ A. 0.90 B. ‎0.30 ‎C. 0.60 D. 0.40‎ ‎【答案】D ‎【解析】依题意,射中环及以上的概率为,故不够环的概率为.‎ 二、填空题（共4小题，将答案填在答题卡上）‎ ‎13.用辗转相除法求出153和119的最大公约数是 ．‎ ‎【答案】17‎ ‎【解析】153=119×1+34，119=34×3+17，34=17×2．‎ ‎∴153与119的最大公约数是17．‎ 故答案为17．‎ ‎14.如图是一个算法的程序框图，当输入的值x为8时，则其输出的结果是__________．‎ ‎【答案】2‎ ‎【解析】x=8＞0，不满足条件x≤0，则执行循环体，依此类推，当x=-1＜0，满足条件，退出循环体，从而求出最后的y值即可．解：x=8＞0，执行循环体，x=x-3=5-3=2＞0，继续执行循环体， x=x-3=2-3=-1＜0，满足条件，退出循环体，故输出y=0.5-1=（）-1=2．故答案为2‎ ‎15. 从一批产品中取出三件产品,设A={三件产品全不是次品},B ‎={三件产品全是次品},C={三件产品不全是次品},则下列结论正确的序号是________.‎ ‎①A与B互斥;②B与C互斥;③A与C互斥;④A与B对立;⑤B与C对立.‎ ‎【答案】①②⑤‎ ‎【解析】A为{三件产品全不是次品}，指的是三件产品都是正品，B为{三件产品全是次品}，C为{三件产品不全是次品}，它包括一件次品，两件次品，三件全是正品三个事件，由此知：A与B是互斥事件，但不对立；A与C是包含关系，不是互斥事件，更不是对立事件；B与C是互斥事件，也是对立事件．所以正确结论的序号为①②⑤．‎ 考点：互斥事件对立事件 ‎16.是半径为的圆周上一个定点，在圆周上等可能任取一点，连接，则弦的长度超过的概率是________.‎ ‎【答案】‎ ‎【解析】根据题意可转化为满足条件：“弦的长度超过”对应的弧的概率，‎ 弦的长度等于时，圆心角为，对应弧长,弦的长度超过时所对应圆弧的长为， ‎ 则弦的长度超过的概率是.‎ 故答案为：.‎ 三、解答题（共6小题，将答案填在答题卡上）‎ ‎17.用秦九韶算法求,当时的值.‎ 解：根据秦九韶算法,把多项式改写成如下形式:‎ ‎,‎ 当时.,‎ ‎,‎ ‎,‎ ‎,‎ ‎,‎ ‎,‎ 所以当时,多项式的值为.‎ ‎18.已知.‎ ‎（1）若，求、及的值；‎ ‎（2）求的值.‎ 解：（1）‎ 又因为，‎ ‎ ‎ ‎ ‎ ‎(2) ‎ ‎19.某网站举行“卫生防疫”的知识竞赛网上答题，共有120000人通过该网站参加了这次竞赛，为了解竞赛成绩情况，从中抽取了100人的成绩进行统计，其中成绩分组区间为，，，，，其频率分布直方图如图所示，请你解答下列问题：‎ ‎（1）求的值；‎ ‎（2）成绩不低于90分的人就能获得积分奖励，求所有参赛者中获得奖励的人数；‎ ‎（3）根据频率分布直方图，估计这次知识竞赛成绩的平均分（用组中值代替各组数据的平均值）.‎ 解：（1）由频率分布直方图的性质，可得，‎ 解得.‎ ‎（2）由频率分布直方图，可得成绩在之间的频率为，‎ 所以可估计所有参赛者中获得奖励的人数约为人.‎ ‎（3）根据频率分布直方图的平均数的计算公式，‎ 可得平均分的估计值为分.‎ ‎20.为了展示中华汉字的无穷魅力，传递传统文化，提高学习热情，某校开展《中国汉字听写大会》的活动．为响应学校号召，2（9）班组建了兴趣班，根据甲、乙两人近期8次成绩画出茎叶图，如图所示（把频率当作概率）．‎ ‎（1）求甲、乙两人成绩的平均数和中位数；‎ ‎（2）现要从甲、乙两人中选派一人参加比赛，从统计学的角度，你认为派哪位学生参加比较合适？‎ 解：（1）由茎叶图可知甲、乙两人成绩的平均数为 ‎，‎ ‎，‎ 甲、乙两人成绩的中位数为 ‎，．‎ ‎（2）派甲参加比较合适，理由如下：‎ ‎，‎ ‎ ，‎ ‎∵，，‎ ‎∴两人的平均成绩相等，但甲的成绩比较稳定，派甲参加比较合适．‎ ‎21.某贫困地区截至2018年底，按照农村家庭人均年纯收入8000元的小康标准，该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户，得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图.‎ ‎（1）补全频率分布直方图，并求出这50户家庭人均年纯收入的中位数和平均数（精确到元）；‎ ‎（2）2019年7月，为估计该地能否在2020年全面实现小康，统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如表：‎ 由散点图及相关性分析发现：家庭人均月纯收入与时间代码之间具有较强的线性相关关系，请求出回归直线方程；并由此估计该家庭2020年1月的家庭人均月纯收入.‎ ‎①可能用到的数据：；‎ ‎②参考公式：线性回归方程中，，.‎ 解：（1）由频率之和为1可得：家庭人均年纯收入在的频率为0.18，所以频率分布直方图如下：‎ 中位数为：（千元），‎ 平均数（千元）.‎ ‎（2）解：由题意得：，‎ ‎，‎ ‎，.‎ 所以：.‎ ‎，‎ 所以回归直线方程为：.‎ 估计2020年1月的家庭人均月纯收入：代入得.‎ ‎22.2020年寒假期间新冠肺炎肆虐，全国人民众志成城抗疫情.某市要求全体市民在家隔离，同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”，要求学校各科老师每天在网上授课辅导，每天共200分钟.教育局为了了解高三学生网上学习情况，上课几天后在全区高三学生中采取随机抽样的方法抽取了80名学生（其中男女生恰好各占一半）进行问卷调查，按男女生分为两组，再将每组学生在线学习时间（分钟）分为5组，，，，得到如图所示的频率分布直方图.全区高三学生有3000人（男女生人数大致相等），以频率估计概率回答下列问题：‎ ‎（1）估计全区高三学生中网上学习时间不超过40分钟的人数；‎ ‎（2）在调查的80名高三学生且学习时间不超过40分钟的学生中，男女生按分层抽样的方法抽取6人.若从这6人中随机抽取2人进行电话访谈，求至少抽到1名男生的概率.‎ 解：（1）男生自主学习不超过40分钟的人数：人，‎ 女生自主学习不超过40分钟的人数：人，‎ 所以估计全区高三学生网上学习时间不超过40分钟的人数为225人.‎ ‎（2）在80名学生中，男生网上学习不超过40分钟的人数：人，‎ 女生网上学习不超过40分钟的人数：人，‎ 所以选4名男生，2名女生.‎ ‎4名男生设为，，，，2名女生设为，任选2人有：，，，，，，，，，，，，，，，共15种.‎ 没有男生的有，共1种.‎ 所以至少有一名男生的概率.‎