【数学】宁夏六盘山高级中学2019-2020学年高一下学期期中考试试题 7页

宁夏六盘山高级中学2019-2020学年 高一下学期期中考试试题 第Ⅰ卷 选择题（共60分）‎ 一、选择题（本大题共12小题，每小题5分，满分60分.） ‎ ‎1．在下列各图中，两个变量具有线性相关关系的图是( ).‎ ‎(4)‎ ‎(3)‎ ‎(2)‎ ‎(1)‎ A．(1)(2) B．(1)(3) C．(2)(4) D．(2)(3) ‎ ‎2.要从已编号（1～55）的55枚最新研制的某型号导弹中随机抽取5枚来进行发射试验，用系统抽样方法，确定所选取的5枚导弹的编号可能是（　　）‎ A. B. ‎ C. D.‎ ‎3.掷一枚骰子，则掷得奇数点的概率是（ ）‎ ‎ A.　 B.　 C.　 D.　‎ ‎4.下列事件中是随机事件的个数有（ ）‎ ‎①连续两次抛掷两个骰子，两次都出现2点；②在地球上，树上掉下的雪梨不抓住就往下掉；③某人买彩票中奖；④在标准大气压下，水加热到‎90℃‎会沸腾。‎ ‎ A. B. C. D. 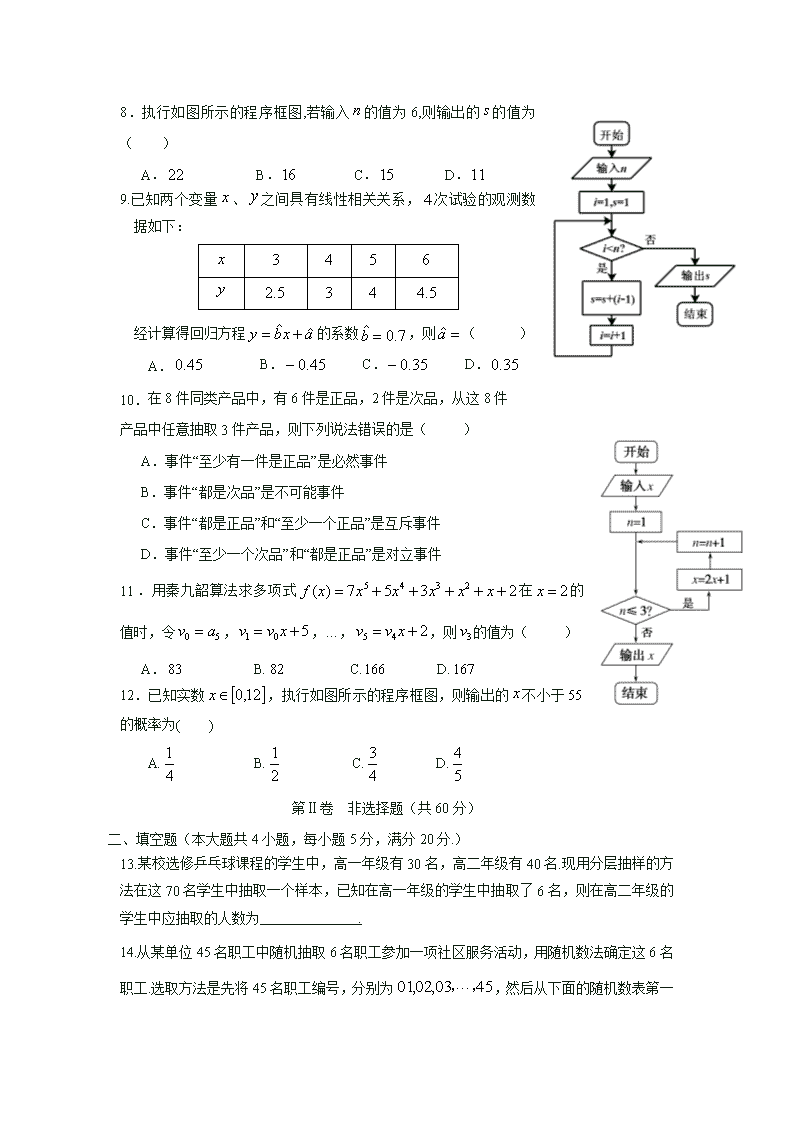‎ ‎5.把22化为二进制数为( ).‎ ‎ A． B． C． D．‎ ‎6.某产品分一、二、三级，其中只有一级品是正品.若生产中出现二级品的概率为，出现三级品的概率为，则出现正品的概率为( )‎ ‎ A． B． C． D．‎ ‎7．与的最大公约数为(　　)‎ ‎ A．　 B． C． D．‎ ‎8．执行如图所示的程序框图,若输入的值为6,则输出的的值为（ ）‎ ‎ A． B． C． D．‎ ‎9.已知两个变量、之间具有线性相关关系，次试验的观测数据如下：‎ 经计算得回归方程的系数，则（　 　）‎ A． ‎ B． C． D．‎ 10． 在8件同类产品中，有6件是正品，2件是次品，从这8件 ‎ 产品中任意抽取3件产品，则下列说法错误的是（ ）‎ ‎ A．事件“至少有一件是正品”是必然事件 ‎ ‎ B．事件“都是次品”是不可能事件 ‎ C．事件“都是正品”和“至少一个正品”是互斥事件 ‎ ‎ D．事件“至少一个次品”和“都是正品”是对立事件 ‎11．用秦九韶算法求多项式在的值时，令，，…，，则的值为（ ）‎ ‎ A． B. C. D.‎ ‎12．已知实数，执行如图所示的程序框图，则输出的不小于的概率为(　　)‎ A.　　　 B. C.　　　 D.‎ 第Ⅱ卷 非选择题（共60分）‎ 二、填空题（本大题共4小题，每小题5分，满分20分.）‎ ‎13.某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为 .‎ ‎14.从某单位45名职工中随机抽取6名职工参加一项社区服务活动，用随机数法确定这6名职工.选取方法是先将45名职工编号，分别为 ‎，然后从下面的随机数表第一行的第5列的数字7开始由左到右依次选取两个数字，从而确定6个个体的编号，则选出的第6个职工的编号为 .‎ ‎16 22 77 94 39　49 54 43 54 82　17 37 93 23 78　87 35 20 96 43‎ ‎84 42 17 53 31　57 24 55 06 88　77 04 74 47 67　21 76 33 50 25‎ ‎15．已知一组数据，，，，的方差为2，则数据，，，， 的方差为 ．‎ ‎16．若采用随机模拟的方法估计某运动员射击击中目标的概率．先由计算器给出0到9之间取整数的随机数，指定0,1,2,3表示没有击中目标，4,5,6,7,8,9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了20组如下的随机数：‎ ‎7327　0293　7140　9857　0347　4373　8636　6947　1417　4698‎ ‎0371　6133　2616　8045　6011　3661　9597　7424　7610　4281‎ 根据以上数据估计该运动员射击4次恰好击中3次的概率为________．‎ 三、解答题：（本大题共4小题，满分40分.解答须写出文字说明、证明过程和演算步骤.）‎ ‎17.（本题满分10分）从甲、乙两种玉米苗中各抽10株，分别测得它们株高如下(单位：cm)：‎ ‎ 问：（1）哪种玉米的苗长得高？‎ ‎（2）哪种玉米的苗长得整齐？‎ ‎18.（本题满分10分）某电脑公司有6名产品推销员，其中5名产品推销员工作年限与年推销金额数据如下表：‎ 推销员编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 工作年限/年 ‎3‎ ‎5‎ ‎6‎ ‎7‎ ‎9‎ 推销金额/万元 ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎ （1）求年推销金额关于工作年限的线性回归方程；‎ ‎ （2）若第6名推销员的工作年限为12年，试估计他的年推销金额．‎ 参考公式：==，‎ ‎19.（本题满分10分）为提高产品质量，某企业质量管理部门经常不定期地抽查产品进行检测，现在某条生产线上随机抽取100个产品进行相关数据的对比，并对每个产品进行综合评分（满分100分），将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品．‎ ‎（1）求图中的值；‎ ‎（2）求综合评分的中位数；‎ ‎（3）用样本估计总体，以频率作为概率，按分层抽样的思想，先在该条生产线中随机抽取5个产品，再从这5个产品中随机抽取2个产品记录有关数据，求这2个产品中至多有一个一等品的概率．‎ ‎20.（本题满分10分）某校举行运动会，其中三级跳远的成绩在‎8.0米 (四舍五入,精确到‎0.1米) 以上的进入决赛，把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30 ，第6小组的频数是7 .‎ ‎（1）求进入决赛的人数；‎ ‎（2）经过多次测试后发现，甲成绩均匀分布在8～10米之间，乙成绩均匀分布在8.5～10‎.5米之间，现甲,乙各跳一次，求甲比乙远的概率.‎ ‎ ‎ ‎ 参考答案 一、选择题 本大题共12小题，每小题5分，共60分．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎ D ‎ D ‎ ‎ B ‎ B ‎ C ‎ B ‎ D ‎ D D C A ‎ B 二、填空题 本大题共4小题，每小题5分，满分20分．‎ ‎13．8 14． 35 15． 8 16． ‎ ks5u 三、解答题 本题共4小题共40分．解答应写出文字说明、演算步骤或推证过程．‎ ‎17．（本小题满分10分）‎ 解：(1)甲＝18(cm)，乙＝19(cm)， ∴甲<乙，乙种玉米的苗长得高 …5分 ‎ ‎ ‎ ‎ (2)s＝10.2(cm2)，s＝8.8(cm2)， ∴s>s，故乙种玉米的苗长得更整齐． …10分 ‎ ‎18.（本小题满分10分）‎ ‎ 解：(1)设所求的线性回归方程为＝bx＋a，‎ 则b＝＝＝0.5， a＝－b＝0.4.‎ ‎∴年推销金额y关于工作年限x的线性回归方程为＝0.5x＋0.4.…5分 ‎(2)由(1)可知，当x＝12时，＝0.5x＋0.4＝0.5×12＋0.4＝6.4(万元)．‎ ‎∴可以估计第6名推销员的年推销金额为6.4万元．…………………10分 ‎19.（本小题满分10分）‎ 解：（1）由频率和为1，得，；…………2分 ‎ （2） 设综合评分的中位数为，则，‎ ‎ 解得 所以综合评分的中位数为82.5．………4分 ‎ ‎（3）由频率分布直方图知，一等品的频率为，即概率为0.6；‎ 所以100个产品中一等品有60个，非一等品有40个，则一等品与非一等品的抽样比为3：2；‎ 所以现抽取5个产品，一等品有3个，记为、、，非一等品2个，记为、；‎ 从这5个产品中随机抽取2个，基本事件为：、、、、、、、、、 共10种；‎ 抽取的这2个产品中恰有一个一等品的事件为：、、、、、共7种，所以所求的概率为. ……………10分 ‎20.（本小题满分10分）‎ ‎（1）第6小组的频率为1－(0.04＋0.10＋0.14＋0.28＋0.30)＝0.14，‎ ‎∴总人数为(人). ‎ ‎∴第4、5、6组成绩均进入决赛，人数为(0.28＋0.30＋0.14)×50＝36(人)‎ 即进入决赛的人数为 .……………………4分 ‎（2）设甲、乙各跳一次的成绩分别为米，则基本事件满足的区域为 事件“甲比乙远的概率”满足的区域为，如图所示. ‎ ‎∴由几何概型. 即甲比乙远的概率为.…………10分