北师大版高三数学复习专题-三角函数、三角恒等变形、解三角形基础达标-第4章第5节 9页

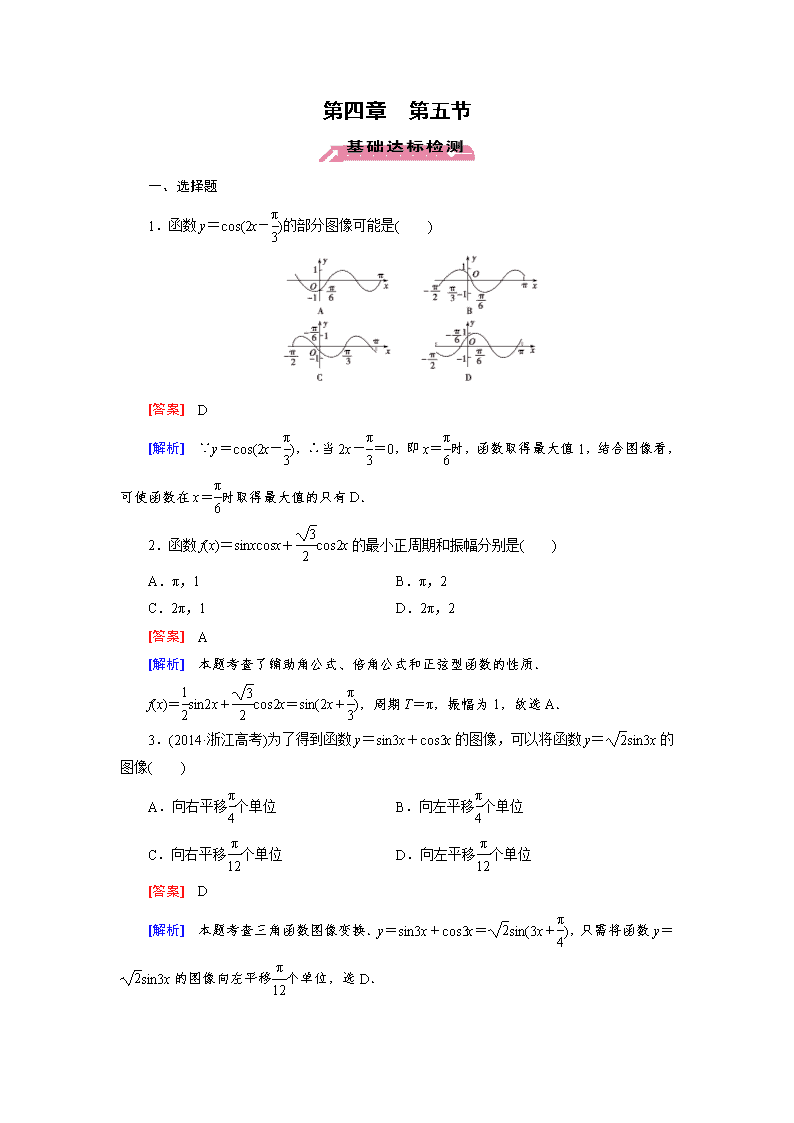
第四章 第五节 一、选择题 1．函数 y＝cos(2x－π 3)的部分图像可能是( ) [答案] D [解析] ∵y＝cos(2x－π 3)，∴当 2x－π 3 ＝0，即 x＝π 6 时，函数取得最大值 1，结合图像看， 可使函数在 x＝π 6 时取得最大值的只有 D． 2．函数 f(x)＝sinxcosx＋ 3 2 cos2x 的最小正周期和振幅分别是( ) A．π，1 B．π，2 C．2π，1 D．2π，2 [答案] A [解析] 本题考查了辅助角公式、倍角公式和正弦型函数的性质． f(x)＝1 2sin2x＋ 3 2 cos2x＝sin(2x＋π 3)，周期 T＝π，振幅为 1，故选 A． 3．(2014·浙江高考)为了得到函数 y＝sin3x＋cos3x 的图像，可以将函数 y＝ 2sin3x 的图 像( ) A．向右平移π 4 个单位 B．向左平移π 4 个单位 C．向右平移 π 12 个单位 D．向左平移 π 12 个单位 [答案] D [解析] 本题考查三角函数图像变换．y＝sin3x＋cos3x＝ 2sin(3x＋π 4)，只需将函数 y ＝ 2sin3x 的图像向左平移 π 12 个单位，选 D． 4．已知函数 y＝sin(ωx＋φ)(ω>0，|φ|<π 2)的部分图像如图所示，则( ) A．ω＝1，φ＝π 6 B．ω＝1，φ＝－π 6 C．ω＝2，φ＝π 6 D．ω＝2，φ＝－π 6 [答案] D [解析] 由图可知T 4 ＝ 7 12π－π 3 ＝π 4 ，T＝π， 即2π ω ＝π，∴ω＝2，又因为图像向右平移了π 2 －π 3 ＝π 6 ，∴φ＝－π 6.(或利用2π 3 ＋φ＝π 2 解也可) 5．已知函数 y＝2sin(ωx＋θ)为偶函数(0<θ<π)，其图像与直线 y＝2 的交点的横坐标为 x1、x2，若|x1－x2|的最小值为π，则( ) A．ω＝2，θ＝π 2 B．ω＝1 2 ，θ＝π 2 C．ω＝1 2 ，θ＝π 4 D．ω＝2，θ＝π 4 [答案] A [解析] y＝2sin(ωx＋θ)为偶函数且 0<θ<π， 所以θ＝π 2 ，y＝2cosωx， ∴y∈[－2,2]．又∵|x1－x2|min＝π， 故 y＝2 与 y＝2cosωx 的交点为最高点，于是最小正周期为π.即2π ω ＝π，所以ω＝2.故选 A． 6．(文)如图，在某点给单摆一个作用力后它开始来回摆动，离开平 衡位置 O 的距离 s(m/s)和时间 t(s)的函数关系为 s＝6sin 2πt＋π 6 ，单摆 摆动时，从最右边到最左边的距离为( ) A．6 3 B．3 3 C．3 D．6 [答案] A [解析] ∵s＝6sin 2πt＋π 6 ，∴T＝2π ω ＝1， 从最左边到平衡位置 O 需要的时间为T 4 ＝1 4s， 由 6sin 2π×1 4 ＋π 6 ＝3 3， 得从最右边到最左边的距离为 6 3. (理)车流量被定义为单位时间内通过十字路口的车辆数，上班高峰某十字路口的车流量 由函数 F(t)＝50＋4sint 2(0≤t≤20)给出，F(t)的单位是辆/分，t 的单位是分，则下列哪个时间 段内车流量是增加的( ) A．[0,5] B．[5,10] C．[10,15] D．[15,20] [答案] C [解析] F(t)的周期为 T＝2π 1 2 ＝4π， 当 2kπ－π 2 ≤t 2 ≤2kπ＋π 2 ，k∈Z 时递增， 即增区间是[4kπ－π，4kπ＋π]，k∈Z，又 0≤t≤20， 故函数 F(t)在[0，π]和[3π，5π]上递增，故选 C． 二、填空题 7．(2014·重庆高考)将函数 f(x)＝sin(ωx＋φ)(ω>0，－π 2 ≤φ<π 2)图像上每一点的横坐标缩 短为原来的一半，纵坐标不变，再向右平移π 6 个单位长度得到 y＝sinx 的图像，则 f(π 6)＝ ________. [答案] 2 2 [解析] 此题考查三角函数图像变换． ∴ω＝1 2 ，φ＝π 6 ∴f(x)＝sin(1 2x＋π 6)，∴f(π 6)＝sinπ 4 ＝ 2 2 . 8．若将函数 y＝2sin(3x＋φ)的图像向右平移π 4 个单位后得到图像关于点(π 3 ，0)对称，则|φ| 的最小值是________． [答案] π 4 [解析] 将函数 y＝2sin(3x＋φ)的图像向右平移π 4 个单位后得到 2sin[3(x－π 4)＋φ]＝ 2sin(3x－3π 4 ＋φ)的图像． 因为该函数的图像关于点(π 3 ，0)对称， 所以 2sin(3×π 3 －3π 4 ＋φ)＝2sin(π 4 ＋φ)＝0， 故有π 4 ＋φ＝kπ(k∈Z)． 解得φ＝kπ－π 4(k∈Z)．当 k＝0 时，|φ|取得最小值π 4. 9．(2014·北京高考)设函数 f(x)＝Asin(ωx＋φ)(A，ω，φ是常数，A>0，ω>0)．若 f(x)在区 间[π 6 ，π 2]上具有单调性，且 f(π 2)＝f(2π 3 )＝－f(π 6)，则 f(x)的最小正周期为________． [答案] π [解析] 本题考查了正弦型函数的单调性对称性以及周期的概念． 由 f(x)在区间[π 6 ，π 2]上具有单调性，且 f(π 2)＝－f(π 6)知，f(x)有对称中心(π 3 ，0)，由 f(π 2)＝f(2 3π) 知 f(x)有对称轴 x＝1 2(π 2 ＋2π 3 )＝7π 12 ，记 T 为最小正周期，则 1 2T≥π 2 －π 6 ⇒T≥2π 3 ，从而7π 12 －π 3 ＝T 4 ⇒T＝π. 三、解答题 10．(文)设函数 f(x)＝sinx＋sin(x＋π 3)． (1)求 f(x)的最小值，并求使 f(x)取得最小值的 x 的集合； (2)不画图，说明函数 y＝f(x)的图像可由 y＝sinx 的图像经过怎样的变化得到． [解析] (1)因为 f(x)＝sinx＋1 2sinx＋ 3 2 cosx＝3 2sinx＋ 3 2 cosx＝ 3sin(x＋π 6)． 所以当 x＋π 6 ＝2kπ－π 2 ，即 x＝2kπ－2π 3 (k∈Z)时，f(x)取最小值－ 3. 此时 x 的取值集合为{x|x＝2kπ－2π 3 ，k∈Z}． (2)先将 y＝sinx 的图像上所有点的纵坐标伸长到原来的 3倍(横坐标不变)，得 y＝ 3sinx 的图像；再将 y＝ 3sinx 的图像上所有的点向左平移π 6 个单位，得 y＝f(x)的图像． (理)已知函数 f(x)＝4cosωx·sin(ωx＋π 4)(ω>0)的最小正周期为π (1)求ω的值； (2)讨论 f(x)在区间[0，π 2]上的单调性． [解析] (1)f(x)＝4cosωx·sin(ωx＋π 4)＝2 2sinxω·cosωx＋2 2cos2ωx ＝ 2(sin2ωx＋cos2ωx)＋ 2＝2sin(2ωx＋π 4)＋ 2. 因为 f(x)的最小正周期为π，且ω>0， 从而有2π 2ω ＝π，故ω＝1. (2)由(1)知 f(x)＝2sin(2x＋π 4)＋ 2. 若 0≤x≤π 2 ，则π 4 ≤2x＋π 4 ≤5π 4 . 当π 4 ≤2x＋π 4 ≤π 2 ，即 0≤x≤π 8 时，f(x)单调递增； 当π 2 ≤2x＋π 4 ≤5π 4 ，即π 8 ≤x≤π 2 时，f(x)单调递减． 综上可知，f(x)在区间[0，π 8]上单调递增， 在区间[π 8 ，π 2]上单调递减. 一、选择题 1．若函数 y＝sin(ωx＋φ)(ω>0)的部分图像如图，则ω＝( ) A．5 B．4 C．3 D．2 [答案] B [解析] 本题考查正弦型函数的图像性质．由图像知，函数周期为 2×(x0＋π 4 －x0)＝π 2 ， ∴2π ω ＝π 2 ，∴ω＝4. 2．(文)定义行列式运算|a1 a2 a3 a4|＝a1a4－a2a3.将函数 f(x)＝|sin2x 3 cos2x 1 |的图像向左平移π 6 个单位，以下是所得函数图像的一个对称中心的是( ) A．(π 4 ，0) B．(π 2 ，0) C．(π 3 ，0) D．( π 12 ，0) [答案] B [解析] 根据行列式的定义可知 f(x)＝sin2x－ 3cos2x＝2sin(2x－π 3)，向左平移π 6 个单位 得到 g(x)＝2sin[2(x＋π 6)－π 3]＝2sin2x，所以 g(π 2)＝2sin(2×π 2)＝2sinπ＝0，所以(π 2 ，0)是函数的 一个对称中心，选 B． (理)动点 A(x，y)在圆 x2＋y2＝1 上绕坐标原点沿逆时针方向匀速旋转，12 秒旋转一周， 已知时间 t＝0 时，点 A 的坐标是(1 2 ， 3 2 )，则当 0≤t≤12 时，动点 A 的纵坐标 y 关于 t(单位： 秒)的函数的单调递增区间是( ) A．[0,1] B．[1,7] C．[7,12] D．[0,1]和[7,12] [答案] D [解析] ∵T＝12，∴ω＝2π 12 ＝π 6 ， 从而设 y 关于 t 的函数为 y＝sin(π 6t＋φ)． 又∵t＝0 时，y＝ 3 2 ，∴φ＝π 3 ，∴y＝sin(π 6t＋π 3)， ∴2kπ－π 2 ≤π 6t＋π 3 ≤2kπ＋π 2 ， 即 12k－5≤t≤12k＋1，k∈Z 时，y 递增． ∵0≤t≤12，∴函数 y 的单调递增区间为[0,1]和[7,12]． 二、填空题 3．(文)已知函数 f(x)＝－ 3sin2x＋sinxcosx，则 f 25π 6 ＝________. [答案] 0 [解析] 解法 1：f(x)＝－ 3×1－cos2x 2 ＋1 2sin2x＝－ 3 2 ＋1 2sin2x＋ 3 2 cos2x ＝－ 3 2 ＋sin 2x＋π 3 ， ∴f 25 6 π ＝－ 3 2 ＋sin26 3 π＝－ 3 2 ＋sin2π 3 ＝－ 3 2 ＋ 3 2 ＝0. 解法 2：当 x＝25π 6 时，f 25 6 π ＝－ 3sin225π 6 ＋sin25π 6 cos25π 6 ＝－ 3sin2π 6 ＋sinπ 6cosπ 6 ＝－ 3 4 ＋1 2 × 3 2 ＝0. (理)函数 y＝3sin x 2 －π 6 的对称中心是____________． [答案] π 3 ＋2kπ，0 ，k∈Z [解析] 由x 2 －π 6 ＝kπ，k∈Z 得x 2 ＝π 6 ＋kπ. ∴x＝π 3 ＋2kπ，k∈Z. ∴对称中心是 π 3 ＋2kπ，0 (k∈Z)． 4．如图所示为函数 y＝Asin(ωx＋φ)的图像上的一段，则这个函数的解析式为 ______________． [答案] y＝2sin 3x 2 －3π 4 [解析] A＝2，T 2 ＝5π 6 －π 6 ＝2π 3 ，T＝4π 3 ， ∵2π ω ＝4 3π，∴ω＝3 2 ，∴y＝2sin 3 2x＋φ . ∵当 x＝5 6π时，y＝2，∴2＝2sin 3 2 ×5 6π＋φ ， 即 sin φ＋5 4π ＝1，∴φ＋5 4π＝π 2 ，φ＝－3π 4 ， ∴y＝2sin 3 2x－3π 4 . 三、解答题 5．(文)(2015·广东联考)已知函数 f(x)＝sin(2x＋π 6)＋sin(2x－π 6)－cos2x＋a(a∈R，a 为常 数)． (1)求函数 f(x)的最小正周期和单调增区间； (2)若函数 f(x)的图像向左平移 m(m>0)个单位后，得到函数 g(x)的图像关于 y 轴对称，求 实数 m 的最小值． [解析] (1)f(x)＝sin(2x＋π 6)＋sin(2x－π 6)－cos2x＋a＝ 3sin2x－cos2x＋a＝2sin(2x－π 6)＋ A． ∴f(x)的最小正周期为2π 2 ＝π， 当 2kπ－π 2 ≤2x－π 6 ≤2kπ＋π 2(k∈Z)， 即 kπ－π 6 ≤x≤kπ＋π 3(k∈Z)时，函数 f(x)单调递增， 故所求函数 f(x)的单调增区间为[kπ－π 6 ，kπ＋π 3](k∈Z)． (2)函数 f(x)的图像向左平移 m(m>0)个单位后得 g(x)＝2sin[2(x＋m)－π 6]＋a 要使 g(x)的图 像关于 y 轴对称，只需 2m－π 6 ＝kπ＋π 2(k∈Z)． 即 m＝kπ 2 ＋π 3(k∈Z)，所以 m 的最小值为π 3. (理)已知函数 f(x)＝ 3sinωx·cosωx－cos2ωx(ω>0)的周期为 π 2. (1)求ω的值和函数 f(x)的单调递增区间； (2)设△ABC 的三边 a、b、c 满足 b2＝ac，且边 b 所对的角为 x，求此时函数 f(x)的值域． [解析] (1)f(x)＝ 3 2 sin2ωx－1 2(cos2ωx＋1)＝sin(2ωx－π 6)－1 2 ， 由 f(x)的周期 T＝2π 2ω ＝π 2 ，得ω＝2， ∴f(x)＝sin(4x－π 6)－1 2 ， 由 2kπ－π 2 ≤4x－π 6 ≤2kπ＋π 2(k∈Z)， 得－ π 12 ＋kπ 2 ≤x≤π 6 ＋kπ 2 (k∈Z)， 即 f(x)的单调递增区间是[－ π 12 ＋kπ 2 ，π 6 ＋kπ 2 ](k∈Z)． (2)由题意，得 cosx＝a2＋c2－b2 2ac ≥2ac－ac 2ac ＝1 2 ， 又∵011 时，实验室需要降温． 由(1)得 f(t)＝10－2sin( π 12t＋π 3)， 故有 10－2sin( π 12t＋π 3)>11，即 sin( π 12t＋π 3)<－1 2. 又 0≤t<24，因此7π 6 < π 12t＋π 3<11π 6 ，即 10