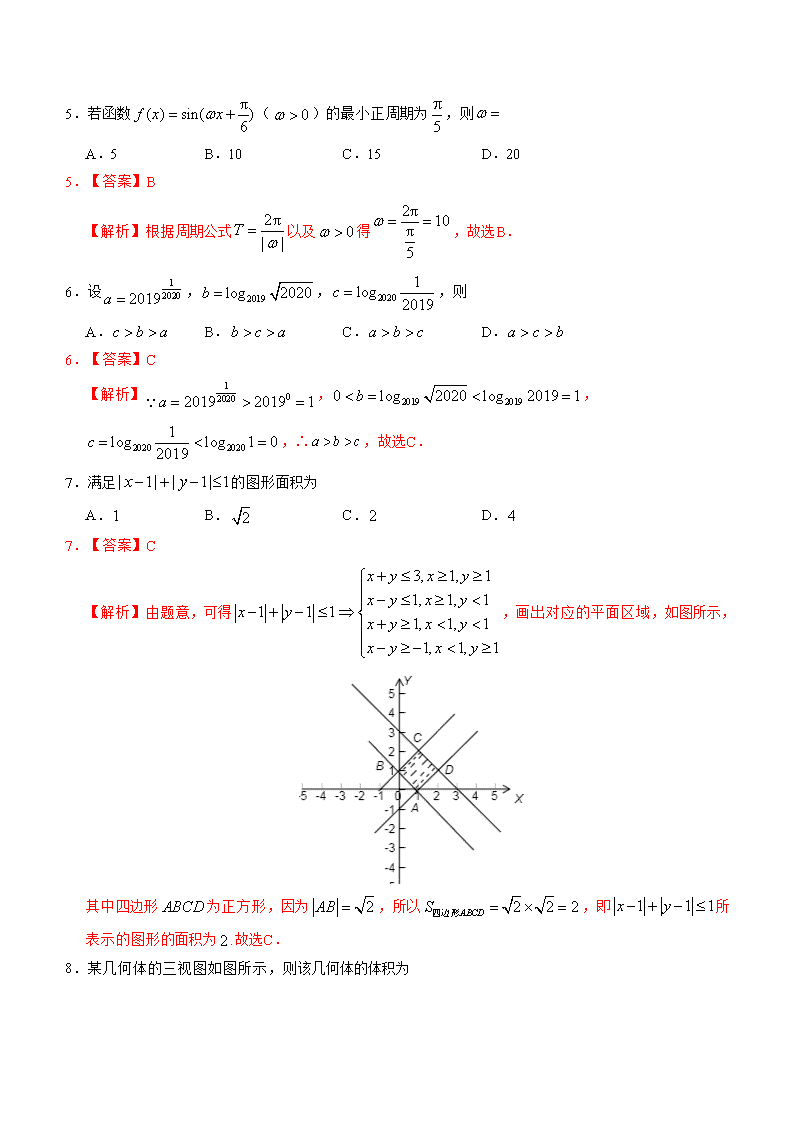2020年1月浙江省普通高中学业水平考试数学模拟试题B 解析版 11页

‎2020年1月浙江省普通高中学业水平考试 数学仿真模拟试题B· 解析版 选择题部分 一、选择题（本大题共18小题，每小题3分，共54分，每小题列出的四个选项中只有一个是符合题目要求的，不选、多选、错选均不得分）‎ ‎1．已知集合，，则 A． B． C． D．‎ ‎1．【答案】C ‎【解析】易得，，‎ 所以.故选C．‎ ‎2．已知，是实数，则“”是“”的 A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既非充分也不必要条件 ‎2．【答案】B ‎【解析】当，时，，但不满足，故不是充分条件；‎ 由不等式的性质可知， 由可得，故是必要条件.故选B．‎ ‎3．设函数，则 A．−1 B．0 C．1 D．3‎ ‎3．【答案】B ‎【解析】因为，所以，故选B．‎ ‎4．设是双曲线上的动点，则到该双曲线两个焦点的距离之差的绝对值为 A．4 B． C． D．‎ ‎4．【答案】A ‎【解析】由题得.由双曲线的定义可知到该双曲线两个焦点的距离之差的绝对值为.故选A.‎ ‎5．若函数（）的最小正周期为，则 A．5 B．10 C．15 D．20‎ ‎5．【答案】B ‎【解析】根据周期公式以及得，故选B．‎ ‎6．设，，，则 A． B． C． D．‎ ‎6．【答案】C ‎【解析】，，‎ ‎，∴，故选C．‎ ‎7．满足的图形面积为 A． B． C． D．‎ ‎7．【答案】C ‎【解析】由题意，可得，画出对应的平面区域，如图所示，‎ 其中四边形为正方形，因为，所以，即所表示的图形的面积为.故选C． ‎ ‎8．某几何体的三视图如图所示，则该几何体的体积为 A． B． C． D．‎ ‎8．【答案】A ‎【解析】由题意，根据给定的几何体的三视图可知，该几何体的左侧是一个底面半径为1，母线长为2的半圆柱，右侧是一个底面半径为1，高为1的半圆锥，所以该几何体的体积为，故选A．‎ ‎9．已知是等差数列，且，，则=‎ A．−12 B．−11 C．−6 D．−5‎ ‎9．【答案】C ‎【解析】因为数列是等差数列，所以公差，‎ 所以，解得，故选C．‎ ‎10．若向量，，则 A． B． C．3 D．‎ ‎10．【答案】D ‎【解析】由题得，则=，故选D．‎ ‎11．已知、为两条不同的直线，、为两个不同的平面，，，则下列结论不可能成立的是 A．，且 B．，且 C．，且 D．与、都相交 ‎11．【答案】D ‎【解析】如图，正方体中，令平面为平面，平面为平面，则为直线，，不妨设为直线，‎ 平面平面，平面，且，即A项成立；‎ 同理满足，且，即B项成立；‎ 平面，平面，平面，即，，且成立，即C选项成立.‎ 故排除A，B，C．‎ 对于D，若，且，则或， 所以不可能与相交，同理，不可能与相交，故D不可能成立.‎ 故选D．‎ ‎12．已知圆的圆心在轴的正半轴上，点在圆上，且圆被直线截得的弦长为，则圆的方程为 A． B．‎ C． D．‎ ‎12．【答案】B ‎【解析】由题意，设圆心坐标为（），因为在圆上，所以圆的半径为，又圆心到直线的距离为，且圆被直线截得的弦长为，所以，解得，所以，因此，所求圆的方程为.故选B．‎ ‎13．若两个非零向量、，满足，则向量与的夹角为 A． B． C． D．‎ ‎13．【答案】C ‎【解析】由得：，又，所以向量与的夹角满足，解得，故选C．‎ ‎14．在中，角，，的对边分别为，，，，，则的值为 A．2 B．3 C．4 D．5‎ ‎14．【答案】C ‎【解析】由，及正弦定理得，‎ 由余弦定理得，，即，‎ 又，所以，即，又，所以.故选C．‎ ‎15．已知函数有三个零点，则 A．4 B．6 C．8 D．12‎ ‎15．【答案】C ‎【解析】画出与的图象如下图所示：‎ ‎，‎ 由有三个零点，得当时方程在区间内有两个相等的实根，所以，得或，‎ 若，，舍去；若，满足条件，所以；‎ 当时，的两根之积为，所以，‎ 所以，故选C．‎ ‎16．设二次函数，若对任意的实数，都存在实数使得不等式成立，则实数的取值范围是 A． B．‎ C． D．‎ ‎16．【答案】D ‎【解析】问题条件的反面为“若存在实数，对任意实数使得不等式成立”，即 只要在上的最大值与最小值之差小于2即可.‎ 当，得；当，得；当.‎ 所以.‎ 综上可得，所求实数的取值范围是，故选D．‎ ‎17．平面直角坐标系中，是抛物线的焦点，点在抛物线上，且满足，，则为 A． B． C． D．‎ ‎17．【答案】A ‎【解析】设，则，‎ 由得，‎ 因为，所以结合，，得，‎ 因此，‎ 从而，‎ 故选A．‎ ‎18．如图，在菱形ABCD中，，线段AD，BD，BC的中点分别为E，F，K，连接EF，FK ‎．现将绕对角线BD旋转，令二面角A－BD－C的平面角为，则在旋转过程中有 A． B． C． D．‎ ‎18．【答案】B ‎【解析】如图，绕旋转形成以圆为底面的两个圆锥(为圆心，为半径，为的中点)，，，‎ 当且时，与等腰中，为公共边，且，，.‎ 当时，，‎ 当时，，‎ 综上，，即.‎ C、D选项比较与的大小关系，由图可知即比较与的大小关系，根据特殊值验证：当时，，当时，，∴C、D都不正确.‎ 故选B．‎ 非选择题部分 二、填空题（本大题共4小题，每空3分，共15分）‎ ‎19．已知，若，则______；______.‎ ‎19．【答案】;‎ ‎【解析】，‎ ‎，所以，.‎ ‎20．已知直线，若，则______.‎ ‎20．【答案】1或−3‎ ‎【解析】因为l1⊥l2，所以k·（k﹣1）+（1﹣k）·（2k+3）＝0，解得 k＝1或k＝﹣3，故答案为1或﹣3.‎ ‎21．已知向量，，，，若，则的最小值为______.‎ ‎21．【答案】‎ ‎【解析】∵，∴，即，‎ ‎∵，，∴，​当且仅当时取等号，‎ ‎∴的最小值是．故答案为．‎ ‎22．已知数列满足，，为数列的前项和，则满足不等式的的最大值为______.‎ ‎22．【答案】8‎ ‎【解析】对变形得：，即，故可以分析得到数列是首项为12，公比为的等比数列.‎ 所以，，‎ 所以，‎ 故，解得最大正整数.‎ 三、解答题（本大题共3小题，共31分）‎ ‎23．（本小题满分10分）‎ 在中，内角、、所对的边分别为、、，已知，.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）设，解不等式.‎ ‎23．（本小题满分10分）‎ ‎【解析】（Ⅰ）因为，所以，‎ 又，所以.（3分）‎ 所以.（5分）‎ ‎（Ⅱ）因为，，所以.（6分）‎ 所以，（8分）‎ 解得，.（10分）‎ ‎24．（本小题满分10分）‎ 已知椭圆的焦距为4，点P（2，3）在椭圆上．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过点P引圆的两条切线PA，PB，切线PA，PB与椭圆C的另一个交点分别为A，B，试问直线AB的斜率是否为定值？若是，求出其定值；若不是，请说明理由．‎ ‎24．（本小题满分10分）‎ ‎【解析】（Ⅰ）因为椭圆C的焦距为4，所以c＝2，则左焦点为F1（﹣2，0），右焦点为F2（2，0），‎ 所以|PF1|＝5，|PF2|＝3，所以2a＝|PF1|+|PF2|＝5+3＝8，即，（2分）‎ 所以b2=a2−c2=12，‎ 故椭圆C的方程为．（4分）‎ ‎（Ⅱ）设PA： ，则，所以；‎ 设PB：，则，所以，‎ 所以，为方程的两根，即．（6分）‎ 设，，联立， ‎ 有，‎ ‎，．‎ 同理联立，可得：，（8分）‎ 则．‎ 故直线AB的斜率是定值，且定值为.（10分）‎ ‎25．（本小题满分11分）‎ 已知函数.‎ ‎（Ⅰ）当时，求在时的值域；‎ ‎（Ⅱ）若对任意，，均有，求的取值范围.‎ ‎25．（本小题满分11分）‎ ‎【解析】（Ⅰ）当时，，‎ 因为，所以，则，‎ 所以在时的值域为.（3分）‎ ‎（Ⅱ）依题意对任意，，恒成立，‎ 所以在时恒成立，则.（5分）‎ 对任意，函数在区间上单调递减，‎ 由已知，均有，‎ 所以在时恒成立，‎ 即在时恒成立.（7分）‎ ‎①当，时，，则符合题意.（8分）‎ ‎②当时，在时恒成立，则在时恒成立，‎ 令，所以则.（10分）‎ 由①、②可得的取值范围为.（11分）‎