- 136.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时分层作业(十一) 基本不等式的应用
(建议用时:40分钟)
一、选择题
1.若a>1,则a+的最小值是( )
A.2 B.a
C. D.3
D [∵a>1,∴a-1>0,∴a+=a-1++1≥
2+1=3.]
2.已知f(x)=x+-2(x<0),则f(x)有( )
A.最大值为0 B.最小值为0
C.最大值为-4 D.最小值为-4
C [∵x<0,∴f(x)=--2≤-2-2=-4,当且仅当-x=,即x=-1时取等号.]
3.已知a>0,b>0,ab=1,且m=b+,n=a+,则m+n的最小值是( )
A.3 B.4
C.5 D.6
B [由题意知ab=1,∴m=b+=2b,n=a+=2a,∴m+n=2(a+b)≥4=4,当且仅当a=b=1时取等号.]
4.若x>0,y>0,且+=1,则x+y的最小值是( )
A.3 B.6
C.9 D.12
C [x+y=(x+y)=1+++4
=5++≥5+2=5+4=9.
当且仅当即时等号成立,故x+y的最小值为9.]
5.已知x>0,y>0,且x+y=8,则(1+x)(1+y)的最大值为( )
- 5 -
A.16 B.25
C.9 D.36
B [(1+x)(1+y)≤
===25,
因此当且仅当1+x=1+y,即x=y=4时,
(1+x)(1+y)取最大值25,故选B.]
二、填空题
6.函数y=x+(x≥0)的最小值为___________.
[答案] 1
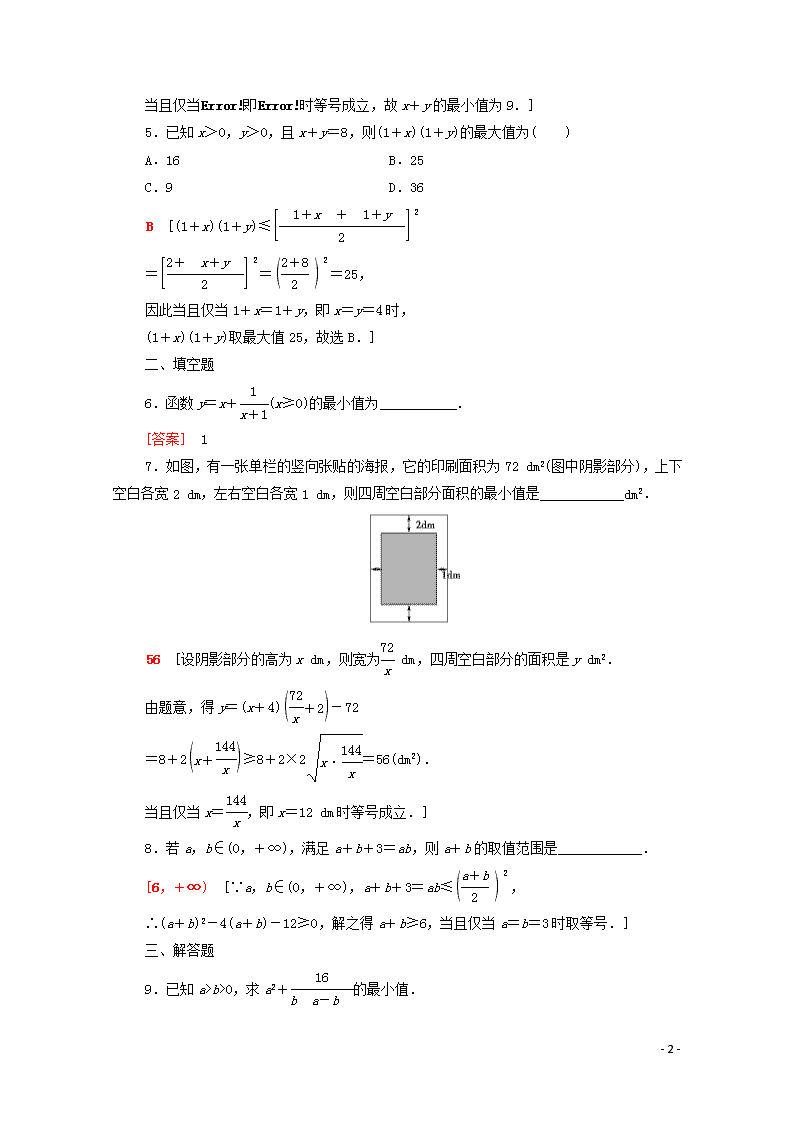
7.如图,有一张单栏的竖向张贴的海报,它的印刷面积为72 dm2(图中阴影部分),上下空白各宽2 dm,左右空白各宽1 dm,则四周空白部分面积的最小值是____________dm2.
56 [设阴影部分的高为x dm,则宽为 dm,四周空白部分的面积是y dm2.
由题意,得y=(x+4)-72
=8+2≥8+2×2=56(dm2).
当且仅当x=,即x=12 dm时等号成立.]
8.若a,b∈(0,+∞),满足a+b+3=ab,则a+b的取值范围是____________.
[6,+∞) [∵a,b∈(0,+∞),a+b+3=ab≤,
∴(a+b)2-4(a+b)-12≥0,解之得a+b≥6,当且仅当a=b=3时取等号.]
三、解答题
9.已知a>b>0,求a2+的最小值.
[解] ∵a>b>0,
所以b(a-b)≤=,
- 5 -
∴a2+≥a2+≥16.
当且仅当即时取等号.
故a2+的最小值为16.
10.为了改善居民的居住条件,某城建公司承包了棚户区改造工程,按合同规定在4个月内完成.若提前完成,则每提前一天可获2 000元奖金,但要追加投入费用;若延期完成,则每延期一天将被罚款5 000元.追加投入的费用按以下关系计算:6x+-118(千元),其中x表示提前完工的天数,试问提前多少天,才能使公司获得最大附加效益?(附加效益=所获奖金-追加费用)
[解] 设城建公司获得的附加效益为y千元,由题意得
y=2x-=118-
=118-
=130-
≤130-2=130-112=18(千元),
当且仅当4(x+3)=,即x=11时取等号.
所以提前11天,能使公司获得最大附加效益.
1.若-40.
故f(x)=-≤-1.
当且仅当x-1=,即x=0时等号成立.]
2.已知x>0,y>0,且+=1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
A.(-∞,-2]∪[4,+∞) B.(-∞,-4]∪[2,+∞)
C.(-2,4) D.(-4,2)
- 5 -
D [∵x>0,y>0且+=1,
∴x+2y=(x+2y)=4++
≥4+2=8,当且仅当=,
即x=4,y=2时取等号,∴(x+2y)min=8,要使x+2y>m2+2m恒成立,只需(x+2y)min>m2+2m恒成立,
即8>m2+2m,解得-4
相关文档
- 【数学】2021届一轮复习人教版(文)第2021-06-1611页
- 【数学】2018届一轮复习人教A版不2021-06-166页
- 2018届二轮复习 不等式 课件(全2021-06-1628页
- 2019届二轮复习第3练 不等式与合2021-06-1643页
- 【数学】2018届一轮复习人教A版二2021-06-1613页
- 高中数学人教a必修5学业分层测评172021-06-166页
- 2020届 二轮复习 集合、简易逻2021-06-161页
- 2018届二轮复习 不等式学案(全国通2021-06-1613页
- 【数学】2020届一轮复习(理)江苏专版2021-06-165页
- 高中数学人教a版选修4-5同步辅导与2021-06-1632页