2020届四川泸县一中高三下学期第一次在线月考数学（文）试题（原卷版） 6页

‎2020年春四川省泸县第一中学高三第一学月考试 文科数学 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上.‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.‎ ‎3．考试结束后，将本试卷和答题卡一并交回.‎ 一、选择题：本题共12小题，每小题5分，共60分.在每小题给的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合A＝{﹣1，0，1，2}，B＝{x|（x+1）（x﹣2）＜0}，则A∩B＝（　　）‎ A. {0，1} B. {﹣1，0} C. {﹣1，0，1} D. {0，1，2}‎ ‎2.若，均为实数，且，则（ ）‎ A. B. C. D. ‎ ‎3.已知四边形是平行四边形，点为边的中点，则 A. B. ‎ C. D. ‎ ‎4.已知等差数列{an}的前n项和为Sn，且a2=4，a4=2，则S6=（　　）‎ A. 0 B. 10 C. 15 D. 30‎ ‎5.函数的图象大致为（ ）‎ A. B. ‎ C. D. ‎ ‎6.已知向量，满足，，且，则向量与的夹角的余弦值为（ ）‎ A. B. C. D. ‎ ‎7.已知角的终边经过点，则 A. B. C. D. 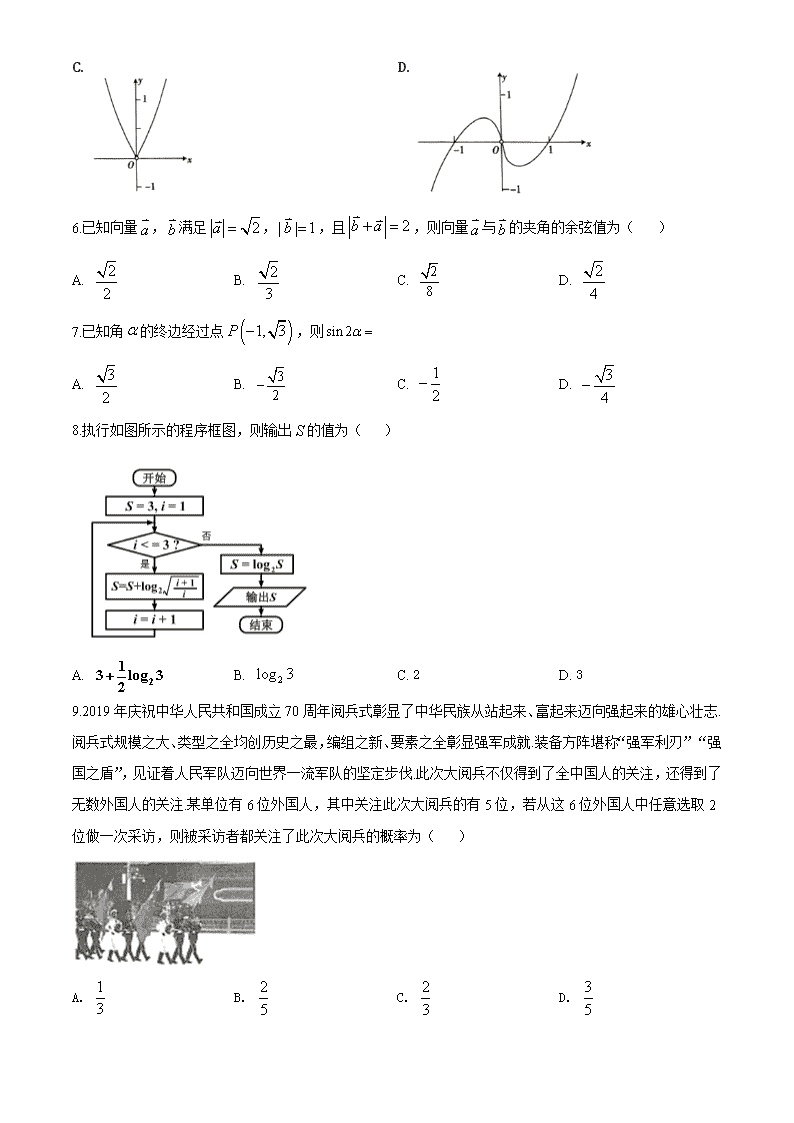‎ ‎8.执行如图所示的程序框图，则输出的值为（ ）‎ A. B. C. 2 D. 3‎ ‎9.2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最，编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”，见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注，还得到了无数外国人的关注.某单位有6位外国人，其中关注此次大阅兵的有5位，若从这6位外国人中任意选取2位做一次采访，则被采访者都关注了此次大阅兵的概率为（ ）‎ A. B. C. D. ‎ ‎10.将函数图像向右平移个周期后，所得图像对应的函数为，则函数的单调递增区间为（ ）‎ A. B. ‎ C. D. ‎ ‎11.若直线是曲线的一条切线，则实数( )‎ A. B. C. D. ‎ ‎12.已知函数是定义在上的函数，且满足，其中为的导数，设，，，则、、的大小关系是　　‎ A. B. C. D. ‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13.已知实数满足条件，则的最大值是__________．‎ ‎14.已知向量，的夹角为，且，，则__________．‎ ‎15.已知矩形 ABCD，AB= 4 ，BC =3，以 A, B 为焦点，且 过 C, D 两点的双曲线的离心率为____________.‎ ‎16.三棱锥中，底面是边长为的等边三角形， 面， ,则三棱锥外接球的表面积是_____________ .‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.‎ ‎（一）必考题：共60分.‎ ‎17.已知某产品的历史收益率的频率分布直方图如图所示.‎ ‎（1）试估计该产品收益率的中位数；‎ ‎（2）若该产品的售价（元）与销量（万份）之间有较强线性相关关系，从历史销售记录中抽样得到如表5组与的对应数据：‎ 售价（元）‎ ‎25‎ ‎30‎ ‎38‎ ‎45‎ ‎52‎ 销量（万份）‎ ‎7.5‎ ‎7.1‎ ‎60‎ ‎5.6‎ ‎4.8‎ 根据表中数据算出关于线性回归方程为，求的值；‎ ‎18.在中，角所对的边分别是满足：，且成等比数列.‎ ‎(Ⅰ)求角的大小；‎ ‎(Ⅱ)若,判断三角形的形状.‎ ‎19.在四棱柱中，底面为平行四边形，平面．，‎ ‎ ‎ ‎（1）证明：平面平面；‎ ‎（2）若直线与底面所成角为， ，，分别为，，的中点，求三棱锥的体积．‎ ‎20.已知椭圆：的离心率为，焦距为．‎ ‎（1）求方程；‎ ‎（2）若斜率为的直线与椭圆交于，两点（点，均在第一象限），为坐标原点，证明：直线，，的斜率依次成等比数列．‎ ‎21.设函数，‎ ‎(1)当时，求函数的单调区间；‎ ‎(2)若在内有极值点，当，，求证：.‎ ‎（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.‎ ‎22.在直角坐标系中，曲线的参数方程为（为参数）,以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求曲线普通方程与曲线的的直角坐标方程；‎ ‎（2）若与交于两点，点的极坐标为，求的值.‎ ‎23.已知函数．‎ ‎（1）求不等式的解集；‎ ‎（2）设函数的最小值为m，当a，b，，且时，求的最大值．‎