浙江专用2021届高考数学一轮复习第八章立体几何8-4直线平面垂直的判定与性质课件 18页

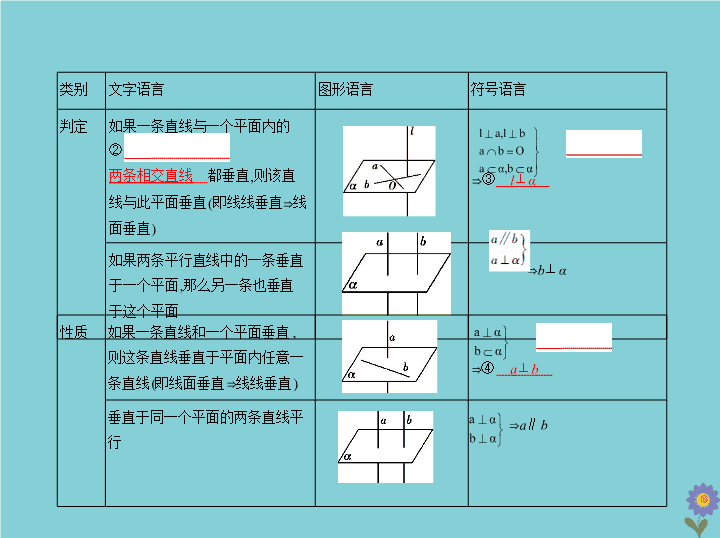
§8.4 直线、平面垂直的判定与性质 高考数学 考点一　直线与平面垂直的判定与性质 　　1.直线与平面垂直 (1)直线与平面垂直的定义 如果直线 l 和平面 α 内的① 　任意一条     直线都垂直,我们就说直线 l 与平面 α 垂直,记作 l ⊥ α . (2)直线与平面垂直的判定和性质 考点 清单 类别 文字语言 图形语言 符号语言 判定 如果一条直线与一个平面内的 ② 　两条相交直线     都垂直,则该直线与此平面垂直(即线线垂直 ⇒ 线面垂直)     ⇒ ③      l ⊥ α      如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面     ⇒ b ⊥ α 性质 如果一条直线和一个平面垂直,则这条直线垂直于平面内任意一条直线(即线面垂直 ⇒ 线线垂直)     ⇒ ④      a ⊥ b      垂直于同一个平面的两条直线平行     ⇒ a ∥ b 2.直线与平面所成的角 (1)定义:平面的一条斜线和它在平面上的射影所成的⑤ 　锐角     叫做这条 直线和这个平面所成的角.一条直线垂直于平面,我们说它们所成的角是直 角;一条直线和平面平行,或在平面内,我们说它们所成的角是0 ° 的角. (2)线面角 θ 的取值范围:0 ° ≤ θ ≤ 90 ° . 常用结论　(1)过一点有且只有一条直线与已知平面垂直. (2)过一点有且只有一个平面与已知直线垂直. 直线 l 和平面 α 的位置关系 l ⊂ α 或 l ∥ α l ⊥ α l 和 α 斜交 θ (直线 l 与平面 α 所成的角)的取值范围 θ =0 ° θ =90 ° 0 ° < θ <90 ° 考点二　平面与平面垂直的判定与性质 　　1.二面角的平面角 从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二 面角的棱,这两个半平面叫做二面角的面.如果记棱为 l ,那么两个面分别为 α 、 β 的二面角记作 α - l - β . 在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱 的射线,则两射线所构成的角叫做二面角的平面角. 类别 文字语言 图形语言 符号语言 判定 两个平面相交,如果它 们所成的二面角是直 二面角,就说这两个平 面互相垂直   ∠ AOB 是二面角 α - l - β 的 平面角,且∠ AOB =90 ° , 则 α ⊥ β 如果一个平面过另一 个平面的垂线,则这两 个平面互相垂直(即线 面垂直 ⇒ 面面垂直)     ⇒ ⑥      β ⊥ α      2.面面垂直的判定和性质 性质 如果两个平面垂直,则 其中一个平面内垂直 于交线的直线垂直于 另一个平面     ⇒ l ⊥ α 如果两个相交平面同 时垂直于第三个平面, 那么它们的交线垂直 于第三个平面     ⇒ l ⊥ γ 知识拓展    垂直问题的转化方向图   在垂直关系中,线面垂直是核心,已知线面垂直,既可为证明线线垂直提供 依据,又可为利用判定定理证明面面垂直做好铺垫.应用面面垂直的性质定 理时,一般需作辅助线,基本作法是过其中一个平面内一点作交线的垂线, 从而把面面垂直问题转化为线面垂直问题,进而可转化为线线垂直问题. 考法一 　证明直线与平面垂直的方法 知能拓展 例1 　如图,在四棱锥 P - ABCD 中, PA ⊥底面 ABCD , AB ⊥ AD , AC ⊥ CD ,∠ ABC =60 ° , PA = AB = BC , E 是 PC 的中点.求证: (1) CD ⊥ AE ; (2) PD ⊥平面 ABE .   解题导引 　(1)结合已知条件分析可知,欲证 CD ⊥ AE ,只需证 CD ⊥平面 PAC . (2)欲证 PD ⊥平面 ABE ,只需证 PD 垂直于平面 ABE 内的两条交线即可,结合 条件分别证明 PD ⊥ AE , PD ⊥ AB . 证明　 (1)因为 PA ⊥平面 ABCD , CD ⊂ 平面 ABCD , 所以 PA ⊥ CD . 因为 AC ⊥ CD , PA ∩ AC = A ,所以 CD ⊥平面 PAC . 又 AE ⊂ 平面 PAC ,所以 CD ⊥ AE . (2)由 AB = BC ,∠ ABC =60 ° ,可得△ ABC 是等边三角形,所以 AB = AC ,所以 AC = PA . 因为 E 是 PC 的中点,所以 AE ⊥ PC .由(1)知, AE ⊥ CD ,又 PC ∩ CD = C , 所以 AE ⊥平面 PCD .又 PD ⊂ 平面 PCD ,所以 AE ⊥ PD . 因为 PA ⊥平面 ABCD , AB ⊂ 平面 ABCD ,所以 PA ⊥ AB . 又 AB ⊥ AD , PA ∩ AD = A ,所以 AB ⊥平面 PAD , 又 PD ⊂ 平面 PAD ,所以 AB ⊥ PD . 又 AE ∩ AB = A ,所以 PD ⊥平面 ABE . 方法总结 　证明线面垂直的常用方法及关键 (1)证明直线和平面垂直的常用方法:①判定定理;②垂直于平面的传递性 ( a ∥ b , a ⊥ α ⇒ b ⊥ α );③面面平行的性质( a ⊥ α , α ∥ β ⇒ a ⊥ β );④面面垂直的性 质. (2)证明线面垂直的关键是证线线垂直,而证明线线垂直需借助线面垂直的 性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想. 考法二 　平面与平面垂直的判定与性质问题 例2　 如图,在四棱锥 P - ABCD 中, O 为 AB 的中点,平面 POC ⊥平面 ABCD , AD ∥ BC , AB ⊥ BC , PA = PB = BC = AB =2, AD =3. (1)求证:平面 PAB ⊥平面 ABCD ; (2)求二面角 O - PD - C 的余弦值.   解题导引 　(1)要证平面 PAB ⊥平面 ABCD ,需在其中一个平面内找一条直 线,证其与另一个平面垂直,结合已知,考虑证 PO ⊥平面 ABCD ( PO ⊂ 平面 PAB ),而 PO ⊥ AB 易证,关键证 PO ⊥ CD ;再由已知平面 POC ⊥平面 ABCD ,考 虑两平面垂直的性质.若用性质,需找出其交线 OC ,再找出与 OC 垂直的直线 CD ,此时 CD ⊥平面 POC ,证得 CD ⊥ OP , OP ⊥平面 ABCD 即证. (2)寻找特殊点作出二面角 O - PD - C 的平面角,作出与 PD 垂直的平面是关键, 取 OD 的中点 F ,过 F 作 FG ⊥ PD 于 G ,连接 CG , CF ,易证 PD ⊥平面 CFG ,则∠ CGF 即为二面角 O - PD - C 的平面角,求解直角三角形即得余弦值;当然本问 也可用向量法求解. 解析 　(1)证明:∵ PA = PB , O 为 AB 的中点, AB =2, ∴ PO ⊥ AB , AO = BO =1.过点 C 作 CE ∥ AB 交 AD 于 E ,∵ AD ∥ BC , AB ⊥ BC ,∴四 边形 ABCE 是矩形,∴ AE = BC =2, CE = AB =2,又∵ AD =3,∴ DE =1,∴ CD =   =   ,∵ AD ∥ BC , AB ⊥ BC ,∴ AD ⊥ AB ,在Rt△ BOC 中,由勾股定 理得 OC =   =   =   .在Rt△ AOD 中,由勾股定理得 OD = =   =   ,显然 OD 2 = OC 2 + CD 2 =10,∴ CD ⊥ OC ,∵平面 POC ⊥平面 ABCD ,平面 POC ∩ 平面 ABCD = OC ,∴ CD ⊥平面 POC ,又 PO ⊂ 平面 POC ,∴ CD ⊥ PO ,易知 AB 与 CD 相交,∴ PO ⊥平面 ABCD ,∵ PO ⊂ 平面 PAB ,∴平面 PAB ⊥平面 ABCD . (2)解法一:取 OD 的中点 F ,过 F 作 FG ⊥ PD 于 G ,连接 CG , CF . ∵ OC = CD =   ,∴ CF ⊥ OD .∵ PO ⊥平面 ABCD ,∴ CF ⊥ PO ,又 OD ∩ PO = O ,∴ CF ⊥平面 POD ,∴ CF ⊥ PD ,又∵ FG ⊥ PD , CF ∩ FG = F ,∴ PD ⊥平面 CFG ,∴ PD ⊥ CG ,∴∠ CGF 为二面角 O - PD - C 的平面角. ∵ OP =   =   , OD =   ,∠ POD =90 ° , ∴ PD =   ,又∵ DF =   OD =   , ∴ FG = DF ·sin∠ PDO =   ×   =   , 又∵ CF =   =   =   , ∴ CG =   =   =   =   , ∴cos∠ CGF =   =   ÷   =   ×   =   . 故二面角 O - PD - C 的余弦值为   . 解法二:如图,建立空间直角坐标系 O - xyz ,   则 P (0,0,   ), D (-1,3,0), C (1,2,0),∴   =(0,0,   ),   =(-1,3,0),   =(-1,-2,   ),   =(-2,1,0). 设平面 OPD 的法向量为 n 1 =( x 1 , y 1 , z 1 ), 平面 PCD 的法向量为 n 2 =( x 2 , y 2 , z 2 ). 由   可得   取 y 1 =1,得 x 1 =3,即 n 1 =(3,1,0). 由   可得   取 x 2 =   ,得 y 2 =2   , z 2 =5,即 n 2 =(   ,2   ,5), ∴cos< n 1 , n 2 >=   =   =   , 故二面角 O - PD - C 的余弦值为   . 方法总结     证明面面垂直的常用方法 1.利用面面垂直的定义(作出两平面构成的二面角的平面角,计算平面角为 90 ° ); 2.利用面面垂直的判定定理: a ⊥ β , a ⊂ α ⇒ α ⊥ β . 3.证明两个平面垂直,通常是通过证明线线垂直→线面垂直→面面垂直来 实现的,因此,在关于垂直问题的论证中要注意线线垂直、线面垂直、面面 垂直的相互转化.