- 908.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
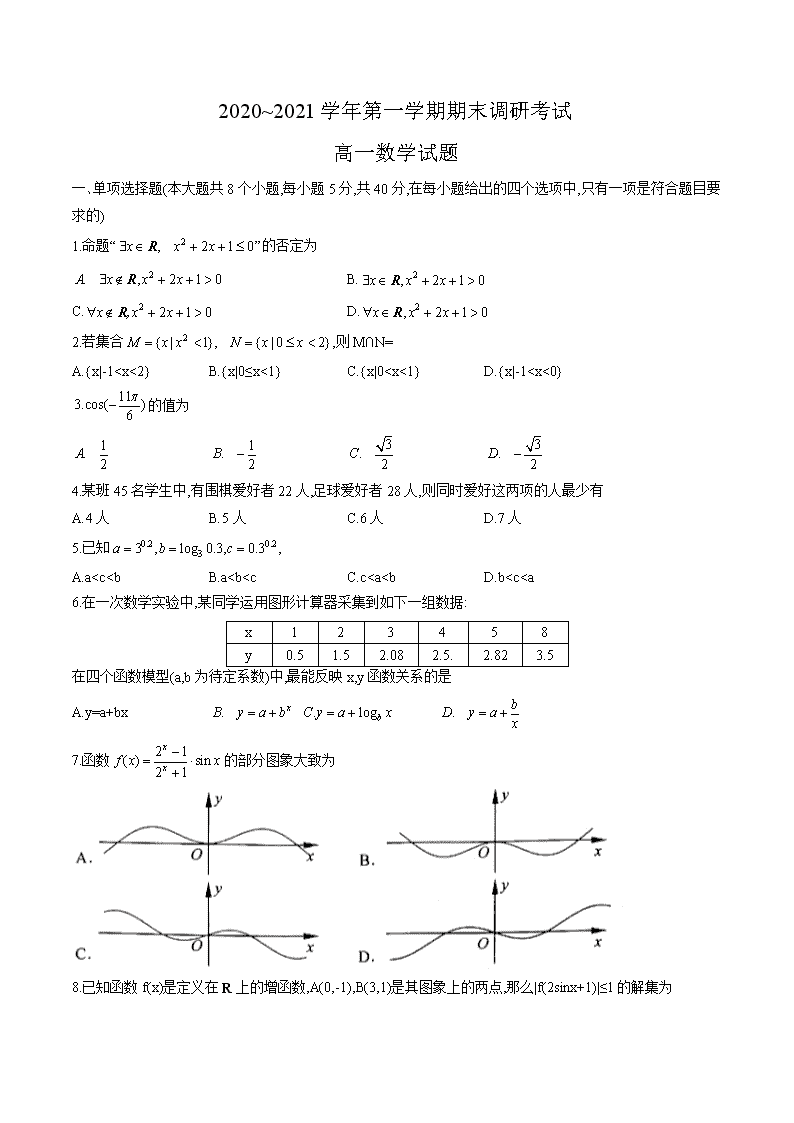
2020~2021学年第一学期期末调研考试
高一数学试题
一、单项选择题(本大题共 8个小题,每小题 5分,共 40分,在每小题给出的四个选项中,只有一项是符合题目要
求的)
1.命题“ 2, 2 1 0x x x R ”的否定为
2. , 2 1 0A x x x R B. 2, 2 1 0x x x R
C. 2 2 1 0x x x R, D. 2, 2 1 0x x x R
2.若集合 2{ | 1}, 0 2{ | }M x x N x x ,则M∩N=
A.{x|-1bc,则 a>b B.若 a>|b|,则 2 2a b
C.若 a>b>0,则 1
1
b b
a a
D.若 a<|b|;则 2 2a b
10.若 x>0,y>0,n≠0,m∈R,则下列各式中,恒等的是
A.lgx+lgy=lg(x+y) .lg lg lgxB x y
y
. log logn
m
xx
mC y y
n
1 lg. lg n xD x
n
11.一半径为 4米的水轮如图所示,水轮圆心 O距离水面 2米,已知水轮每 60秒逆时针转动一圈,如果当水轮上
点 P从水中浮现时(图中点 0P )开始计时,则
A.点 P第一次到达最高点需要 20秒
B.当水轮转动 155秒时,3.点 P距离水面 2米
C.当水轮转动 50秒时,点 P在水面下方,距离水面 2米
D.点 P距离水面的高度 h (米)与 t(秒)的函数解析式为 4sin( ) 2
30 6
h t
12.已知函数 f(x),x∈(-∞,0)∪(0,+∞),对于任意的 x,y∈(-∞,0)∪(0,+∞),f(xy)=f(x)+f(y),则
A.f(x)的图象过点(1,0)和(-1,0)
B.f(x)在定义域上为奇函数
C.若当 x>1时,有 f(x)>0,则当-10的解集(1,∞)
三、填空题(本大题共 4个小题,每小题 5分,共 20分)
13.已知函数
1
2
2 2, 1
( ) log , 1,
x x
f x x x
则 f(f(1))=___.
14.函数 ( ) 3sin(2 )
3
f x x
的减区间是___.
15.若函数 2( ) 2f x x ax 在区间(-1,1)上有两个不同的零点,则实数 a的取值范围是___.
16.某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的 0.25%.
已知在过滤过程中的污染物的残留数量 P(单位:毫克/升)与过滤时间 t(单位:小时)之间的函数关系为
0
ktP P e 其中 e是自然对数的底数,k为常数, 0P 为原污染物总量).若前 4个小时废气中的污染物被过滤掉了
80%,则 k=____;
要能够按规定排放废气,还需要过滤 n小时,则正整数 n的最小值为__.
(参考数据: 5log 2 0.43 )
四、解答题(本大题共 6个小题,共 70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分 10分)
在①角α的终边经过点 P(4m,- 3m)(m≠0); 3tan( )
2 4
② ③3sinα+4cosα=0这三个条件中任选一个,
求 2 2sin sin cos 2cos 的值.
注:如果选择多个条件分别作答,按第一个解答计分.
18.(本小题满分 12分)
已知集合 2{ | log ( 1) 2}A x x ,集合. 2 2{ | 2 1 0}B x x ax a .,其中 a∈R.
(1)若 a=1,求 A∪B;
(2)若“x∈A”是“x∈B”的必要条件,求 a的取值范围.
19.(本小题满分 12分)
受疫情的影响及互联网经济的不断深化,网上购物已经逐渐成为居民购物的新时尚,为迎接 2021年“庆元旦”
网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销,经调查测算,该促销产品在“庆元旦”网购
狂欢节的销售量 p (万件)与促销费用 x(万元)满足
43
2
p
x
(其中 0≤x≤10),已知生产该产品还需投入成本
(10+2p)万元(不含促销费用),每一件产品的销售价格定为
20(6 )
p
元,假定厂家的生产能力能满足市场的销售
需求.
(1)将该产品的利润 y(万元)表示为促销费用 x(万元).的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润.
20.(本小题满分 12分)
已知函数 2( ) 2cos sin 1( )f x x a x a a R 的最小值为 g(a),且 1(
2
) .g a
(1)求实数 a的值;
(2)求函数 f(x)的最大值,并求此时 x的取值集合.
21.(本小题满分 12分)
已知函数 f(x)=2cos(ωx+φ)(ω>0,0 <φ<π)的部分图象如图所示.
(1)求函数 f(x)的解析式;
(2)将函数 f(x)图象上每个点的横坐标变为原来的 2倍(纵坐标不变),再将得到的图象向右平移 4个单位长度,
所得图象的函数为 g(x),若不等式 g(x)-m≤0在 x∈[0,6]恒成立,求实数 m的取值范围.
22.(本小题满分 12分)
已知 a∈R,函数 2
1( ) log ( ).f x a
x
(1)设 a>0,若对任意
1[ ,1],
4
t 函数 f(x)在区间[t,t+1]上的最大值与最小值的差不超过 2,求 a的最小值;
(2)若关于 x的方程 2( ) log [( 2) 3 5] 0
2
xf a x a 的解集中恰好只有一个元素,求 a的取值范围.
相关文档
- 2012年江苏高考试题(数学解析版)2021-06-1520页
- 2019年江苏高考数学考试说明-22021-06-1526页
- 2020江苏高考名篇默写44篇(修订版)2021-06-078页
- 2021版江苏高考物理一轮复习讲义:第2021-06-0126页
- 2008年江苏高考物理试题+全解全析2021-05-2419页
- 2021版江苏高考物理一轮复习课后限2021-05-2214页
- 2020届江苏高考英语二轮培优新方案2021-05-2113页
- 2020届江苏高考英语二轮培优新方案2021-05-2028页
- 2020届江苏高考英语二轮培优新方案2021-05-1931页
- 江苏高考生物模拟试题2021-05-1410页