高中数学（人教版a版必修三）配套单元检测：第三章 单元检测 a卷 word版含答案 9页

第三章 概 率(A) (时间：120 分钟 满分：150 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分) 1．下列事件中不是随机事件的是( ) A．某人购买福利彩票中奖 B．从 10 个杯子(8 个正品，2 个次品)中任取 2 个，2 个均为次品 C．在标准大气压下，水加热到 100℃沸腾 D．某人投篮 10 次，投中 8 次 2．某班有男生 25 人，其中 1 人为班长，女生 15 人，现从该班选出 1 人，作为该班的代 表参加座谈会，下列说法中正确的是( ) ①选出 1 人是班长的概率为 1 40 ； ②选出 1 人是男生的概率是 1 25 ； ③选出 1 人是女生的概率是 1 15 ； ④在女生中选出 1 人是班长的概率是 0. A．①② B．①③ C．③④ D．①④ 3．同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是( ) A.1 2 B.1 3 C.1 4 D.1 8 4．把红、黑、蓝、白 4 张纸牌随机地分发给甲、乙、丙、丁四个人，每人分得 1 张，事 件“甲分得红牌”与事件“乙分得红牌”是( ) A．对立事件 B．不可能事件 C．互斥但不是对立事件 D．以上答案都不对 5．在 2010 年广州亚运会火炬传递活动中，在编号为 1,2,3,4,5 的 5 名火炬手．若从中任 选 3 人，则选出的火炬手的编号相连的概率为( ) A. 1 10 B. 3 10 C. 7 10 D. 9 10 6．从装有红球、白球和黑球各 2 个的口袋内一次取出 2 个球，则与事件“两球都为白球” 互斥而非对立的事件是以下事件“①两球都不是白球；②两球恰有一白球；③两球至少 有一个白球”中的哪几个？( ) A．①② B．①③ C．②③ D．①②③ 7．矩形长为 6，宽为 4，在矩形内随机地撒 300 颗黄豆，数得落在阴影部分内的黄豆数 为 204 颗，以此实验数据为依据可以估计出阴影部分的面积约为( ) A．16 B．16.32 C．16.34 D．15.96 8．在区间(15,25]内的所有实数中随机取一个实数 a，则这个实数满足 17n 的概率为( ) A. 7 10 B. 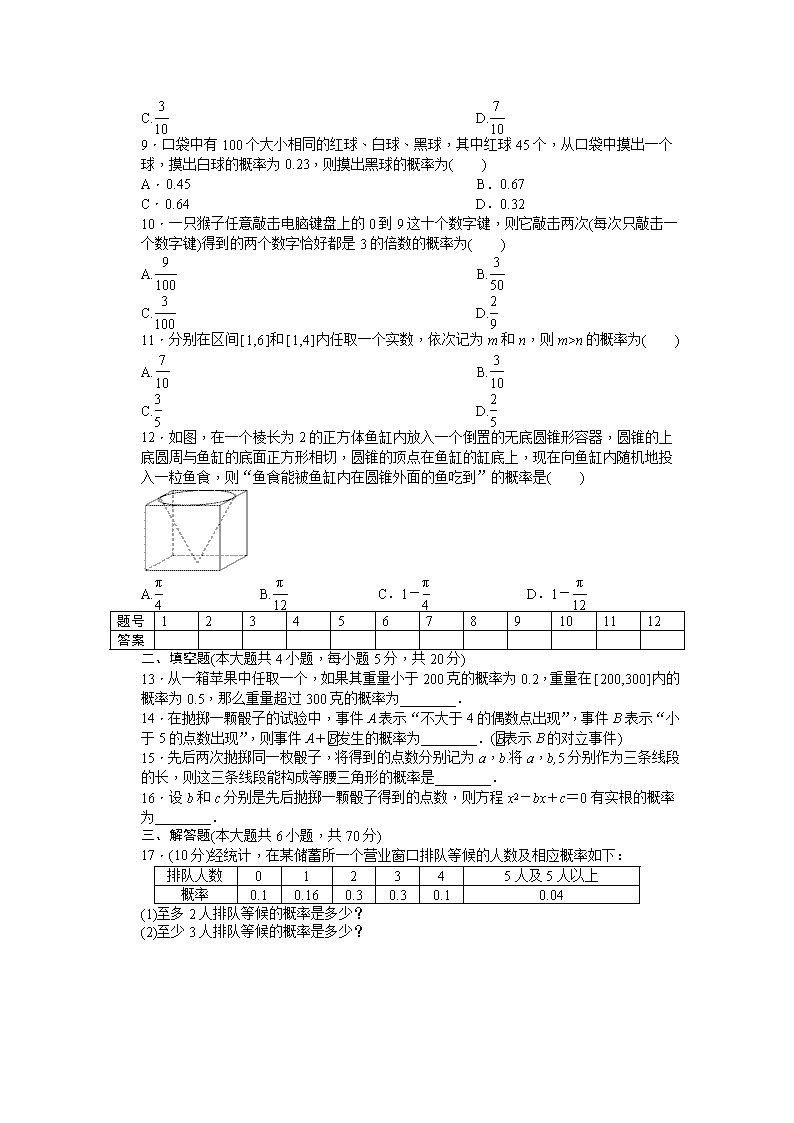3 10 C.3 5 D.2 5 12．如图，在一个棱长为 2 的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的上 底圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投 入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( ) A.π 4 B. π 12 C．1－π 4 D．1－ π 12 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 13．从一箱苹果中任取一个，如果其重量小于 200 克的概率为 0.2，重量在[200,300]内的 概率为 0.5，那么重量超过 300 克的概率为________． 14．在抛掷一颗骰子的试验中，事件 A 表示“不大于 4 的偶数点出现”，事件 B 表示“小 于 5 的点数出现”，则事件 A＋ B 发生的概率为________．( B 表示 B 的对立事件) 15．先后两次抛掷同一枚骰子，将得到的点数分别记为 a，b.将 a，b,5 分别作为三条线段 的长，则这三条线段能构成等腰三角形的概率是________． 16．设 b 和 c 分别是先后抛掷一颗骰子得到的点数，则方程 x2－bx＋c＝0 有实根的概率 为________． 三、解答题(本大题共 6 小题，共 70 分) 17．(10 分)经统计，在某储蓄所一个营业窗口排队等候的人数及相应概率如下： 排队人数 0 1 2 3 4 5 人及 5 人以上 概率 0.1 0.16 0.3 0.3 0.1 0.04 (1)至多 2 人排队等候的概率是多少？ (2)至少 3 人排队等候的概率是多少？ 18．(12 分)为了了解某市工厂开展群众体育活动的情况，拟采用分层抽样的方法从 A，B， C 三个区中抽取 7 个工厂进行调查，已知 A，B，C 区中分别有 18,27,18 个工厂． (1)求从 A，B，C 区中分别抽取的工厂个数； (2)若从抽得的 7 个工厂中随机地抽取 2 个进行调查结果的对比，用列举法计算这 2 个工 厂中至少有 1 个来自 A 区的概率． 19．(12 分)在区间(0,1)上随机取两个数 m，n，求关于 x 的一元二次方程 x2－ nx＋m＝0 有实根的概率． 20．(12 分)某市地铁全线共有四个车站，甲、乙两人同时在地铁第一号车站(首发站)乘车．假 设每人自第 2 号车站开始，在每个车站下车是等可能的．约定用有序实数对(x，y)表示“甲 在 x 号车站下车，乙在 y 号车站下车”． (1)用有序实数对把甲、乙两人下车的所有可能的结果列举出来； (2)求甲、乙两人同在第 3 号车站下车的概率； (3)求甲、乙两人在不同的车站下车的概率． 21．(12 分)在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋， 袋中有 3 只黄色、3 只白色的乒乓球(其体积、质地完全相同)，旁边立着一块小黑板写道： 摸球方法：从袋中随机摸出 3 个球，若摸得同一颜色的 3 个球，摊主送给摸球者 5 元钱； 若摸得非同一颜色的 3 个球，摸球者付给摊主 1 元钱． (1)摸出的 3 个球为白球的概率是多少？ (2)假定一天中有 100 人次摸奖，试从概率的角度估算一下这个摊主一天能赚多少钱？ 22．(12 分)汽车厂生产 A，B，C 三类轿车，每类轿车均有舒适型和标准型两种型号，某 月的产量如下表(单位：辆)： 轿车 A 轿车 B 轿车 C 舒适型 100 150 z 标准型 300 450 600 按类用分层抽样的方法在这个月生产的轿车中抽取 50 辆，其中有 A 类轿车 10 辆． (1)求 z 的值； (2)用分层抽样的方法在 C 类轿车中抽取一个容量为 5 的样本．将该样本看成一个总体， 从中任取 2 辆，求至少有 1 辆舒适型轿车的概率； (3)用随机抽样的方法从 B 类舒适型轿车中抽取 8 辆，经检测它们的得分如下： 9.4,8.6,9.2,9.6，8.7，9.3,9.0，8.2.把这 8 辆轿车的得分看成一个总体，从中任取一个数， 求该数与样本平均数之差的绝对值不超过 0.5 的概率． 第三章 概 率(A) 1．C 2．D [本班共有 40 人，1 人为班长，故①对；而“选出 1 人是男生”的概率为25 40 ＝5 8 ； “选出 1 人为女生”的概率为15 40 ＝3 8 ，因班长是男生，∴“在女生中选班长”为不可能事 件，概率为 0.] 3．C [抛掷两枚质地均匀的硬币，可能出现“正、正”、“反、反”、“正、反”、“反、 正”，因此两个正面朝上的概率 P＝1 4.] 4．C [由互斥事件的定义可知：甲、乙不能同时得到红牌，由对立事件的定义可知：甲、 乙可能都得不到红牌，即“甲、乙分得红牌”的事件可能不发生．] 5．B [从 1,2,3,4,5 中任取三个数的结果有 10 种，其中选出的火炬手的编号相连的事件 有：(1,2,3)，(2,3,4)，(3,4,5)，∴选出的火炬手的编号相连的概率为 P＝ 3 10.] 6．A [从口袋内一次取出 2 个球，这个试验的基本事件空间Ω＝{(白，白)，(红，红)，(黑， 黑)，(红，白)，(红，黑)，(黑，白)}，包含 6 个基本事件，当事件 A“两球都为白球”发 生时，①②不可能发生，且 A 不发生时，①不一定发生，②不一定发生，故非对立事件， 而 A 发生时，③可以发生，故不是互斥事件．] 7．B [由题意S 阴 S 矩 ＝204 300 ，∴S 阴＝204 300 ×24＝16.32.] 8．C [∵a∈(15,25]，∴P(17n 的点应在梯形 OABD 内，所以所 求事件的概率为 P＝S 梯形 OABD S 矩形 OABC ＝ 7 10.] 12．C [P＝正方形面积－圆锥底面积 正方形面积 ＝4－π 4 ＝1－π 4.] 13．0.3 解析 所求的概率 P＝1－0.2－0.5＝0.3. 14.2 3 解析 事件 A 包含的基本事件为“出现 2 点”或“出现 4 点”； B 表示“大于等于 5 的 点数出现”，包含的基本事件为“出现 5 点”或“出现 6 点”．显然 A 与 B 是互斥的， 故 P(A＋ B )＝P(A)＋P( B )＝1 3 ＋1 3 ＝2 3. 15. 7 18 解析 基本事件的总数为 6×6＝36. ∵三角形的一边长为 5， ∴当 a＝1 时，b＝5 符合题意，有 1 种情况； 当 a＝2 时，b＝5 符合题意，有 1 种情况； 当 a＝3 时，b＝3 或 5 符合题意，即有 2 种情况； 当 a＝4 时，b＝4 或 5 符合题意，有 2 种情况； 当 a＝5 时，b∈{1,2,3,4,5,6}符合题意， 即有 6 种情况； 当 a＝6 时，b＝5 或 6 符合题意，即有 2 种情况． 故满足条件的不同情况共有 14 种， 所求概率为14 36 ＝ 7 18. 16.19 36 解析 基本事件总数为 36 个， 若使方程有实根，则Δ＝b2－4c≥0，即 b2≥4c. 当 c＝1 时，b＝2,3,4,5,6； 当 c＝2 时，b＝3,4,5,6； 当 c＝3 时，b＝4,5,6； 当 c＝4 时，b＝4,5,6； 当 c＝5 时，b＝5,6； 当 c＝6 时，b＝5,6. 符合条件的事件个数为 5＋4＋3＋3＋2＋2＝19，因此方程 x2－bx＋c＝0 有实根的概率为 19 36. 17．解 记“有 0 人等候”为事件 A，“有 1 人等候”为事件 B，“有 2 人等候”为事件 C，“有 3 人等候”为事件 D，“有 4 人等候”为事件 E，“有 5 人及 5 人以上等候”为 事件 F，则易知 A、B、C、D、E、F 互斥． (1)记“至多 2 人排队等候”为事件 G， 则 G＝A∪B∪C， 所以 P(G)＝P(A∪B∪C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56. (2)记“至少 3 人排队等候”为事件 H， 则 H＝D∪E∪F， 所以 P(H)＝P(D∪E∪F)＝P(D)＋P(E)＋P(F)＝0.3＋0.1＋0.04＝0.44. 也可以这样解，G 与 H 互为对立事件， 所以 P(H)＝1－P(G)＝1－0.56＝0.44. 18．解 (1)工厂总数为 18＋27＋18＝63，样本容量与总体中的个体数比为 7 63 ＝1 9 ，所以从 A，B，C 三个区中应分别抽取的工厂个数为 2,3,2. (2)设 A1，A2 为在 A 区中抽得的 2 个工厂，B1，B2，B3 为在 B 区中抽得的 3 个工厂，C1， C2 为在 C 区中抽得的 2 个工厂，在这 7 个工厂中随机抽取 2 个，全部可能的结果有：(A1， A2)，(A1，B1)，(A1，B2)，(A1，B3)，(A1，C1)，(A1，C2)，(A2，B1)，(A2，B2)，(A2，B3)， (A2，C1)，(A2，C2)，(B1，B2)，(B1，B3)(B1，C1)，(B1，C2)，(B2，B3)，(B2，C1)，(B2， C2)，(B3，C1)，(B3，C2)，(C1，C2)，共有 21 种． 随机地抽取的 2 个工厂至少有 1 个来自 A 区的结果(记为事件 X)有：(A1，A2)，(A1，B1)， (A1，B2)，(A1，B3)，(A1，C1)，(A1，C2)，(A2，B1)，(A2，B2)，(A2，B3)，(A2，C1)，(A2， C2)共有 11 种，所以这 2 个工厂中至少有 1 个来自 A 区的概率为 P(X)＝11 21. 19.解 在平面直角坐标系中，以 x 轴和 y 轴分别表示 m，n 的值，因为 m，n 在(0,1)内与 图中正方形内的点一一对应，即正方形内的所有点构成全部试验结果的区域． 设事件 A 表示方程 x2－ nx＋m＝0 有实根，则事件 A＝{(m，n)| n－4m≥0 0