人教A版高中数学3-1-1方程的根与函数的零点教案新人教版必修1 5页

3.1.1 方程的根与函数的零点（教学设计） 教学目标： 知识与技能：理解函数（结合二次函数）零点的概念，领会函数零点与相应方程要的关系，掌握零点存在的判定 条件． 过程与方法：零点存在性的判定． 情感、态度、价值观：在函数与方程的联系中体验数学中的转化思想的意义和价值． 教学重点： 重点：零点的概念及存在性的判定． 难点：零点的确定． 一、复习回顾，新课导入 讨论：一元二次方程 )0(02  acbxax 的根与二次函数 )0(2  acbxaxy 数的图象有什么关系？ 先观察几个具体的一元二次方程及其相应的二次函数，分别选取方程有两个不同的根、重根和无实数根三种 类型． 方程 0322  xx 与函数 322  xxy ； 方程 0122  xx 与函数 122  xxy ； 方程 0322  xx 与函数 322  xxy ； 再请同学们解方程，并分别画出三个函数的草图． 一元二次方程 )0(02  acbxax 有两不同根就是相应的二次函数 02  cbxaxy 的图象与 x 轴有 两个不同交点，且其横坐标就是根； 一元二次方程 )0(02  acbxax 有两个重根就是相应的二次函数 02  cbxaxy 的图象与 x 轴一 个交点，且其横坐标就是根； 一元二次方程 )0(02  acbxax 无实数根就是相应的二次函数 02  cbxaxy 的图象与 x 轴没有 交点； 总之，一元二次方程 )0(02  acbxax 的根就是相应的二次函数 02  cbxaxy 的图象与 x 轴的 交点的横坐标． 二、师生互动，新课讲解： 1、函数的零点 对于函数 )(xfy  ，我们把使 0)( xf 的实数 x 叫做函数 )(xfy  的零点（zero point）． 显然，函数 )(xfy  的零点就是方程 0)( xf 的实数根，也就是函数 )(xfy  的图象与 x 轴的交点的横坐 标． 方程 0)( xf 有实数根函数 )(xfy  的图象与 x 轴有交点函数 )(xfy  有零点． 2、函数零点的判定： 研究方程的实数根也就是研究相应函数的零点，也就是研究函数的图象与 x 轴的交点情况。 问题 1： 如果把函数比作一部电影， 那么函数的零点就像是电影的一个瞬间，一个镜头。有时我们会忽略一些 镜头，但是我们仍然能推测出被忽略的片断。现在我有两组镜头（如图，第一组第一行两图，第二组第二行两图）， 哪一组能说明他的行程一定曾渡过河？ 第Ⅰ组能说明他的行程中一定曾渡过河，而第Ⅱ组中他的行程就不一定曾渡过河。 问题 2：将河流抽象成 x 轴，将前后的两个位置视为 A、B 两点。请问当 A、B 与 x 轴怎样的位置关系时，AB 间的 一段连续不断的函数图象与 x 轴一定会有交点？ A、B 两点在 x 轴的两侧。 问题 3： A、B 与 x 轴的位置关系，如何用数学符号（式子）来表示？ A、B 两点在 x 轴的两侧。可以用 f（a）·f（b）<0 来表示。 问题 4： 满足条件的函数图象与 x 轴的交点一定在（a，b）内吗？即函数的零点一定在（a，b ）内吗？ 一定在区间（a，b）上。若交点不在（a，b）上，则它不是函数图象。 通过上述探究，让学生自己概括出零点存在性定理： 一般地，我们有： 如果函数 y＝f（x）在区间[a，b]上的图象是连续不断的一条曲线并且有 f（a）·f（b）<0，那么函数 y＝f（x） 在区间（a，b）内有零点，即存在 c∈（a，b），使得 f（c）=0，这个 c 也就是方程 f（x）＝0 的根． ⑴函数零点的意义： 函数 )(xfy  的零点就是方程 0)( xf 实数根，亦即函数 )(xfy  的图象与 x 轴交点的横坐标． 即：方程 0)( xf 有实数根  函数 )(xfy  的图象与 x 轴有交点  函数 )(xfy  有零点． ⑵函数零点的求法：求函数 )(xfy  的零点： ①（代数法）求方程 0)( xf 的实数根； ②（几何法）对于不能用求根公式的方程，可以将它与函数 )(xfy  的图象联系起来，并利用函数的性质找出零 点． ⑶二次函数的零点： )0(2  acbxaxy ． ① △＞０，方程 02  cbxax 有两不等实根，二次函数的图象与 x 轴有两个交点，二次函数有两个零点． ② △＝０，方程 02  cbxax 有两相等实根（二重根），二次函数的图象与 x 轴有一个交点，二次函数有一个 二重零点或二阶零点． ③ △＜０，方程 02  cbxax 无实根，二次函数的图象与 x 轴无交点，二次函数无零点． 课堂练习：（课本 P88 练习 NO：1） 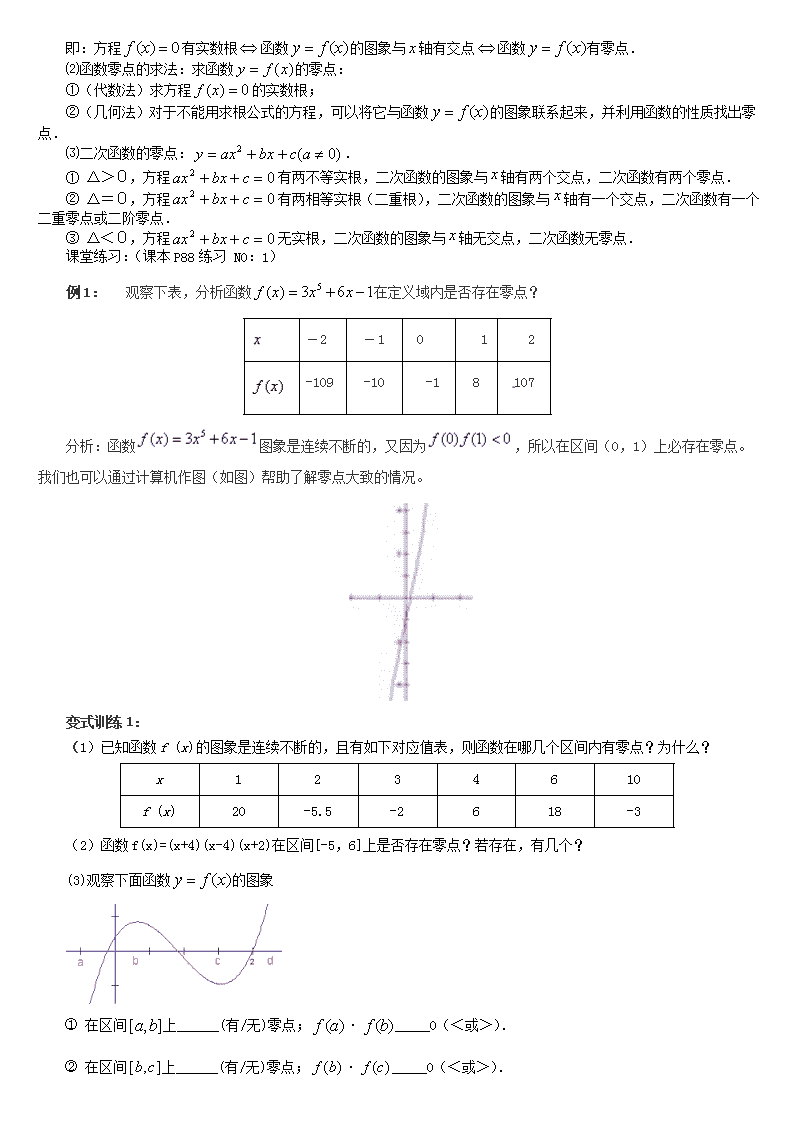例 1： 观察下表，分析函数 5( ) 3 6 1f x x x   在定义域内是否存在零点？ －2 －1 0 1 2 -109 -10 -1 8 107 分析：函数 图象是连续不断的，又因为 ，所以在区间（0，1）上必存在零点。 我们也可以通过计算机作图（如图）帮助了解零点大致的情况。 变式训练 1： （1）已知函数 f (x)的图象是连续不断的，且有如下对应值表，则函数在哪几个区间内有零点？为什么？ x 1 2 3 4 6 10 f (x) 20 -5.5 -2 6 18 -3 （2）函数 f(x)=(x+4)(x-4)(x+2)在区间[-5，6]上是否存在零点？若存在，有几个？ (3)观察下面函数 )(xfy  的图象 ○1 在区间 ],[ ba 上______(有/无)零点； )(af · )(bf _____0（＜或＞）． ○2 在区间 ],[ cb 上______(有/无)零点； )(bf · )(cf _____0（＜或＞）． ○3 在区 间 ],[ dc 上______(有/无)零点； )(cf · )(df _____0（＜或＞） 例 2（课本 P88 例 1）： 求函数 ( ) ln 2 6f x x x   的零点个数． 分析：用计算器或计算机作出 x， 的对应值表和图象。 1 2 3 4 5 6 7 8 9 -4.0 -1.3 1.1 3.4 5.6 7.8 9.9 12.1 14.2 由表可知，f (2)<0，f (3)>0,则 ，这说明函数 在区间（2，3）内有零点。结合函数 的 单调性，进而说明 零点是只有唯一一个． 变式训练 2：利用函数图象判断下列方程有几个根 （1）2x(x-2)=-3 （2） 0xe x  例 3：已知函数 13)( 3  xxxf ，问该函数在区间 )1,2(  内是否有零点？ 解：因为 01)2( f ， 03)1( f ，所以 0)1()2(  ff ，又函数 13)( 3  xxxf 是连续的曲线， 所以 )(xf 在区间 )1,2(  内有零点． 变式训练 3：函数 xxxf 2ln)(  的零点所在的大致区间是（ B ） （A） )2,1( (B) )3,2( (C) )3,(e (D) ),( e 三、课堂小结，巩固反思： 如果函数 )(xfy  在区间 ],[ ba 上的图象是连续不断 的一条曲线，并且在区间端点的函数值符号相反，那么，函 数 )(xfy  在区间 ),( ba 内至少有一个零点，即相应的方程 0)( xf 在区间 ),( ba 内至少有一个实数解． 会用代数法或几何法（特别转化为两条曲线的交点）来判断零点的个数。 四、布置作业： A 组： 1． （课本 P92 习题 3.1 A 组 NO：2） 2． 求下列函数的零点： （1） 452  xxy ；（2） 202  xxy ；（3） )13)(1( 2  xxxy ； （4） )23)(2()( 22  xxxxf ． 3． 求下列函数的零点，图象顶点的坐 标，画出各自的简图，并指出函数值在哪些区间上大于零，哪些区间上小 于零： （1） 123 1 2  xxy ；（2） 142 2  xxy ． 4． 已知 124)1(2)( 2  mmxxmxf ： （1） m 为何值时，函数的图象与 x 轴有两个零点； （2）如果函数至少有一个零点在原点右侧，求 m 的值． 5． 求下列函数的定义域： （1） 92  xy ；（2） 432  xxy ；（3） 1242  xxy 6．设函数 ( ) ln 1f x x x   ．求函数 )(xf 的零 点个数。 B 组： 1、函数 f(x)＝x＋1 x 的零点个数为( A ) A．0 B．1 C．2 D．3 2．若 y＝f(x)在区间[a，b]上的图象为连续不断的一条曲线，则下列说法正确的是( ) A．若 f(a)f(b) <0，不存在实数 c∈(a，b)，使得 f(c)＝0 B．若 f(a)f(b)<0，存在且只存在一个实数 c∈(a，b)，使得 f(c)＝0 C．若 f(a)f(b)>0，不存在实数 c∈(a，b)，使得 f(c)＝0 D．若 f(a)f(b)>0，有可能存在实数 c∈(a，b)，使得 f(c)＝0 答案 D 3．方程 2x＋x＝0 在下列哪个区间内有实数根( ) A．(－2，－1) B．(0,1) C．(1,2 ) D．(－1,0) 答案 D 4．若函数 f(x)唯一的零点在区间(1,3)，(1,4)，(1,5)内，那么下列说法中错误的是( ) A．函数 f(x) 在(1,2)或[2,3)内有零点 B．函数 f(x)在(3,5)内无零点 C．函数 f(x)在(2,5)内有零点 D．函数 f(x)在(2,4)内不一定有零点 答案 C 5．函数 f(x)＝log3x－8＋2x 的零点一定位于区间( ) A．(5,6) B．(3,4) C．(2,3) D．(1,2) 答案 B 解析 f(3)＝log 33－8＋2×3＝－1<0， f(4)＝log34－8＋2×4＝log34>0. 又 f(x)在(0，＋∞)上为增函数， 所以其零点一定位于区间(3,4)．