高考数学大一轮复习第7章第5节直线、平面垂直的判定及其性质课时作业理 7页

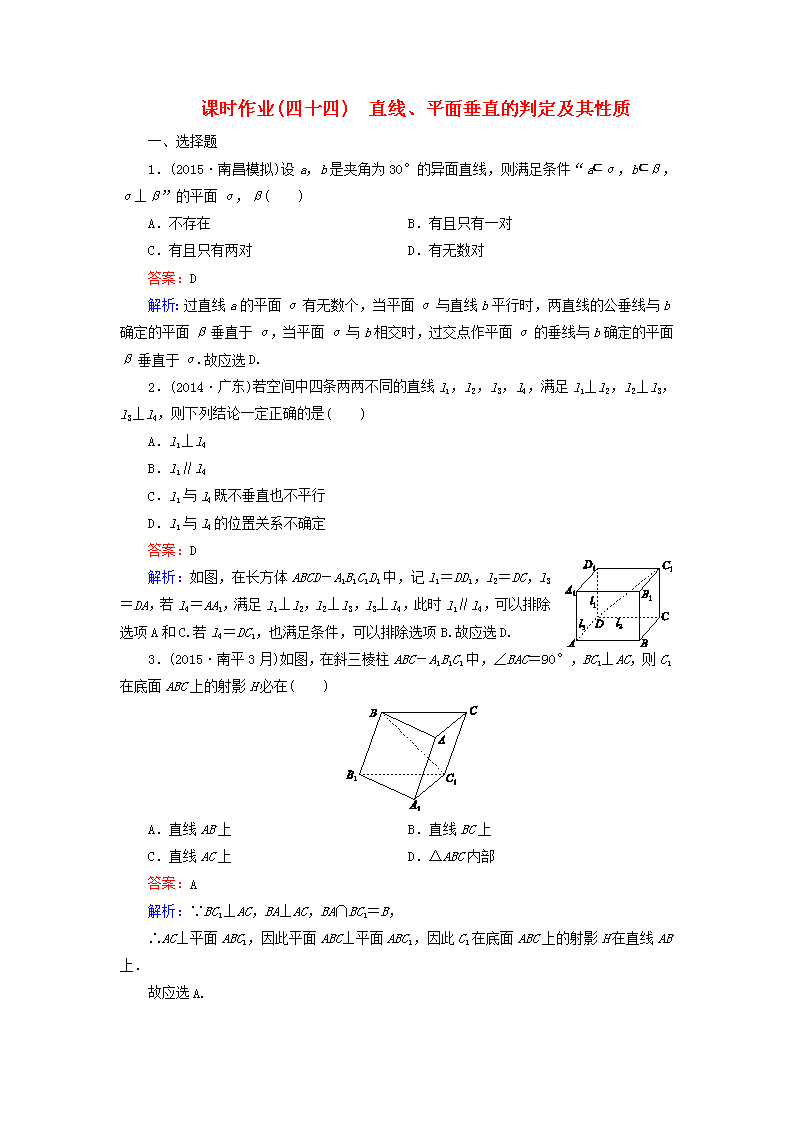
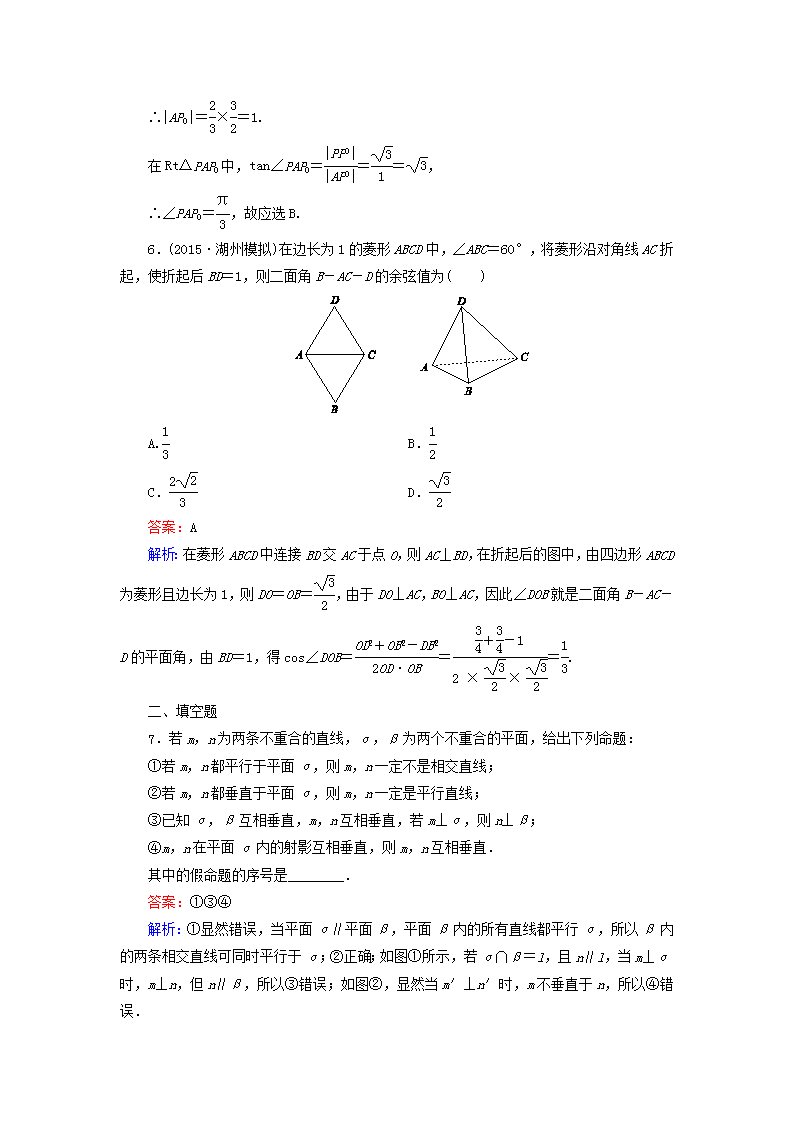
课时作业(四十四) 直线、平面垂直的判定及其性质 一、选择题 1．(2015·南昌模拟)设 a，b 是夹角为 30°的异面直线，则满足条件“a⊂α，b⊂β， α⊥β”的平面α，β( ) A．不存在 B．有且只有一对 C．有且只有两对 D．有无数对 答案：D 解析：过直线 a 的平面α有无数个，当平面α与直线 b 平行时，两直线的公垂线与 b 确定的平面β垂直于α，当平面α与 b 相交时，过交点作平面α的垂线与 b 确定的平面β垂 直于α.故应选 D. 2．(2014·广东)若空间中四条两两不同的直线 l1，l2，l3，l4，满足 l1⊥l2，l2⊥l3，l3 ⊥l4，则下列结论一定正确的是( ) A．l1⊥l4 B．l1∥l4 C．l1 与 l4 既不垂直也不平行 D．l1 与 l4 的位置关系不确定 答案：D 解析：如图，在长方体 ABCD－A1B1C1D1 中，记 l1＝DD1，l2＝DC，l3 ＝DA，若 l4＝AA1，满足 l1⊥l2，l2⊥l3，l3⊥l4，此时 l1∥l4，可以排除 选项 A 和 C.若 l4＝DC1，也满足条件，可以排除选项 B.故应选 D. 3．(2015·南平 3 月)如图，在斜三棱柱 ABC－A1B1C1 中，∠BAC＝90°，BC1⊥AC，则 C1 在底面 ABC 上的射影 H 必在( ) A．直线 AB 上 B．直线 BC 上 C．直线 AC 上 D．△ABC 内部 答案：A 解析：∵BC1⊥AC，BA⊥AC，BA∩BC1＝B， ∴AC⊥平面 ABC1，因此平面 ABC⊥平面 ABC1，因此 C1 在底面 ABC 上的射影 H 在直线 AB 上． 故应选 A. 4．(2015·潍坊模拟)如图，在正四面体 P－ABC 中，D，E，F 分别是 AB，BC，CA 的中 点，下面四个结论不成立的是( ) A．BC∥平面 PDF B．DF⊥平面 PAE C．平面 PDF⊥平面 PAE D．平面 PDE⊥平面 ABC 答案：D 解析：因为 BC∥DF，DF⊂平面 PDF，BC⊄ 平面 PDF，所以 BC∥平面 PDF，A 成立；易证 BC⊥平面 PAE，BC∥DF，所以结论 B，C 均成立；点 P 在底面 ABC 内的射影为△ABC 的中心， 不在中位线 DE 上，故结论 D 不可能成立． 故应选 D. 5．(2013·山东)已知三棱柱 ABC－A1B1C1 的侧棱与底面垂直，体积为9 4 ，底面是边长为 3 的正三角形，若 P 为底面 A1B1C1 的中心，则 PA 与平面 ABC 所成角的大小为( ) A.5π 12 B．π 3 C．π 4 D．π 6 答案：B 解析：如图，设 P0 为底面 ABC 的中心，连接 PP0，由题意知|PP0|为直三棱柱的高，∠PAP0 为 PA 与平面 ABC 所成的角，S△ABC＝1 2 ×( 3)2×sin 60°＝3 3 4 . ∵三棱柱的体积 V＝9 4 ，∴3 3 4 ·|PP0|＝9 4 ，∴|PP0|＝ 3.又 P0 为底面 ABC 的中心，则|AP0| 等于正△ABC 高的2 3 ， 又易知△ABC 的高为3 2 ， ∴|AP0|＝2 3 ×3 2 ＝1. 在 Rt△PAP0 中，tan∠PAP0＝|PP0| |AP0| ＝ 3 1 ＝ 3， ∴∠PAP0＝π 3 ，故应选 B. 6．(2015·湖州模拟)在边长为 1 的菱形 ABCD 中，∠ABC＝60°，将菱形沿对角线 AC 折起，使折起后 BD＝1，则二面角 B－AC－D 的余弦值为( ) A.1 3 B．1 2 C．2 2 3 D． 3 2 答案：A 解析：在菱形 ABCD 中连接 BD 交 AC 于点 O，则 AC⊥BD，在折起后的图中，由四边形 ABCD 为菱形且边长为 1，则 DO＝OB＝ 3 2 ，由于 DO⊥AC，BO⊥AC，因此∠DOB 就是二面角 B－AC －D 的平面角，由 BD＝1，得 cos∠DOB＝OD2＋OB2－DB2 2OD·OB ＝ 3 4 ＋3 4 －1 2× 3 2 × 3 2 ＝1 3 . 二、填空题 7．若 m，n 为两条不重合的直线，α，β为两个不重合的平面，给出下列命题： ①若 m，n 都平行于平面α，则 m，n 一定不是相交直线； ②若 m，n 都垂直于平面α，则 m，n 一定是平行直线； ③已知α，β互相垂直，m，n 互相垂直，若 m⊥α，则 n⊥β； ④m，n 在平面α内的射影互相垂直，则 m，n 互相垂直． 其中的假命题的序号是________． 答案：①③④ 解析：①显然错误，当平面α∥平面β，平面β内的所有直线都平行α，所以β内的两 条相交直线可同时平行于α；②正确；如图①所示，若α∩β＝l，且 n∥l，当 m⊥α时，m ⊥n，但 n∥β，所以③错误；如图②，显然当 m′⊥n′时，m 不垂直于 n，所以④错误． 8. (2015·青岛模拟)如图所示，在四棱锥 P－ABCD 中，PA⊥底面 ABCD，且底面各边都 相等，M 是 PC 上的一动点，当点 M 满足________时，平面 MBD⊥平面 PCD.(只要填写一个你 认为是正确的条件即可) 答案：DM⊥PC(答案不唯一) 解析：由题意，易得 BD⊥PC，所以当 DM⊥PC 时，即有 PC⊥平面 MBD，而 PC⊂平面 PCD， 所以平面 MBD⊥平面 PCD. 9．如图，PA⊥圆 O 所在的平面，AB 是圆 O 的直径，C 是圆 O 上的一点，E，F 分别是点 A 在 PB，PC 上的正投影，给出下列结论： ①AF⊥PB；②EF⊥PB； ③AF⊥BC；④AE⊥平面 PBC. 其中正确结论的序号是________． 答案：①②③ 解析：由题意，知 PA⊥平面 ABC， ∴PA⊥BC. 又 AC⊥BC，PA∩AC＝A， ∴BC⊥平面 PAC. ∴BC⊥AF. ∵AF⊥PC，BC∩PC＝C， ∴AF⊥平面 PBC，∴AF⊥PB，AF⊥BC. 又 AE⊥PB，AE∩AF＝A，∴PB⊥平面 AEF. ∴PB⊥EF.故①②③正确． 10．把等腰直角△ABC 沿斜边上的高 AD 折成直二面角 B－AD－C，则 BD 与平面 ABC 所成 角的正切值为________． 答案： 2 2 解析：如图所示，在平面 ADC 中，过 D 作 DE⊥AC，交 AC 于点 E，连接 BE， 因为二面角 B－AD－C 为直二面角，BD⊥AD，所以 BD⊥平面 ADC，故 BD⊥AC.又 DE∩BD ＝D，因此 AC⊥平面 BDE，又 AC⊂平面 ABC，所以平面 BDE⊥平面 ABC，故∠DBE 就是 BD 与 平面 ABC 所成的角．在 Rt△DBE 中，易求 tan∠DBE＝ 2 2 . 三、解答题 11．(2015·青岛质检)如图所示的几何体中，四边形 ABCD 为矩形，AB＝3BC＝6，BF＝ CF＝AE＝DE＝2，EF＝4，EF∥AB，G 为 FC 的中点，M 为线段 CD 上的一点，且 CM＝2. (1)证明：AF∥平面 BDG； (2)证明：平面 BGM⊥平面 BFC； (3)求三棱锥 F－BMC 的体积 V. 解：(1)证明：如图连接 AC 交 BD 于点 O，则 O 为 AC 的中点，连接 OG. ∵点 G 为 FC 的中点，OG 为△AFC 的中位线， ∴OG∥AF. ∵AF⊄ 平面 BDG，OG⊂平面 BDG， ∴AF∥平面 BDG. (2)证明：如图连接 FM. ∵BF＝CF＝BC＝2，G 为 CF 的中点，∴BG⊥CF. ∵CM＝2，∴DM＝4. ∵EF∥AB，四边形 ABCD 为矩形，∴EF∥DM， 又∵EF＝4，∴四边形 EFMD 为平行四边形． ∴FM＝ED＝2，∴△FCM 为正三角形，∴MG⊥CF. ∵MG∩BG＝G，∴CF⊥平面 BGM. ∵CF⊂平面 BFC，∴平面 BGM⊥平面 BFC. (3)VF－BMC＝VF－BMG＋VC－BMG＝1 3 ×S△BMG×FC ＝1 3 ×S△BMG×2. ∵GM＝BG＝ 3，BM＝2 2， ∴S△BMG＝1 2 ×2 2×1＝ 2， ∴VF－BMC＝2 3 ×S△BMC＝2 2 3 . 12．(2015·汕头模拟)已知四棱锥 PABCD 的直观图和三视图如图所示，E 是侧棱 PC 上 的动点． (1)求四棱锥 P－ABCD 的体积； (2)是否不论点 E 在何位置，都有 BD⊥AE？证明你的结论； (3)若点 E 为 PC 的中点，求二面角 D－AE－B 的大小． 解：(1)由三视图可知，四棱锥 P－ABCD 的底面是边长为 1 的正方形，侧棱 PC⊥底面 ABCD， 且 PC＝2. 所以 VP－ABCD＝1 3 S 正方形 ABCD·PC＝1 3 ×12×2＝2 3 ， 即四棱锥 P－ABCD 的体积为2 3 . (2)不论点 E 在何位置，都有 BD⊥AE. 证明如下：连接 AC，因为 ABCD 是正方形， 所以 BD⊥AC. 因为 PC⊥底面 ABCD，且 BD⊂平面 ABCD， 所以 BD⊥PC. 又因为 AC∩PC＝C， 所以 BD⊥平面 PAC. 因为不论点 E 在何位置，都有 AE⊂平面 PAC. 所以不论点 E 在何位置，都有 BD⊥AE. (3)在平面 DAE 内过点 D 作 DF⊥AE 于 F，连接 BF. 因为 AD＝AB＝1，DE＝BE＝ 12＋12＝ 2， AE＝AE＝ 3， 所以 Rt△ADE≌Rt△ABE， 从而△ADF≌△ABF， 所以 BF⊥AE. 所以∠DFB 为二面角 D－AE－B 的平面角． 在 Rt△ADE 中，DF＝AD·DE AE ＝1× 2 3 ＝ 6 3 ， 所以 BF＝ 6 3 . 又 BD＝ 2，在△DFB 中，由余弦定理，得 cos∠DFB＝DF2＋BF2－BD2 2DF·BF ＝－1 2 ， 所以∠DFB＝2π 3 ， 即二面角 D－AE－B 的大小为2π 3 .