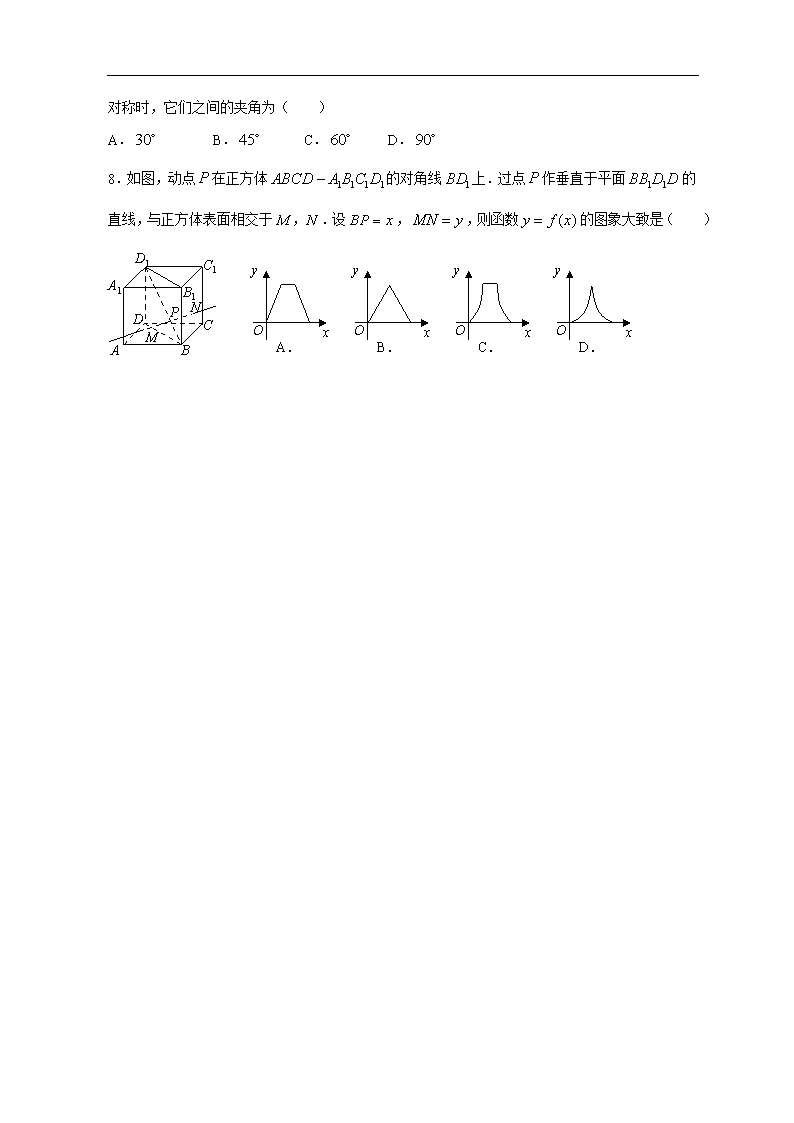高考卷 普通高等学校招生全国统一考试数学（北京卷·理科）（附答案，完全word版） 12页

2008 年普通高等学校招生全国统一考试 数学（理工农医类）（北京卷） 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 9 页，共 150 分．考试时间 120 分钟．考试结束，将本试卷和答题卡一并交回． 第Ⅰ卷（选择题 共 40 分） 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干 净后，再选涂其他答案．不能答在试卷上． 一、本大题共 8 小题，每小题 5 分，共 40 分．在每小题列出的四个选项中，选出符合题目要求 的一项． 1．已知全集U  R ，集合  | 2 3A x x  ≤ ≤ ，  | 1 4B x x x   或 ，那么集合  UA B ð 等于（ ） A． | 2 4x x ≤ B． | 3 4x x x或≤ ≥ C． | 2 1x x  ≤ D． | 1 3x x ≤ ≤ 2．若 0.52a  ， πlog 3b  ， 2 2πlog sin 5c  ，则（ ） A． a b c  B．b a c  C． c a b  D．b c a  3．“函数 ( )( )f x x R 存在反函数”是“函数 ( )f x 在 R 上为增函数”的（ ） A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 4．若点 P 到直线 1x   的距离比它到点 (2 0)， 的距离小 1，则点 P 的轨迹为（ ） A．圆 B．椭圆 C．双曲线 D．抛物线 5．若实数 x y， 满足 1 0 0 0 x y x y x        ， ， ， ≥ ≥ ≤ 则 23x yz  的最小值是（ ） A．0 B．1 C． 3 D．9 6．已知数列 na 对任意的 *p q N， 满足 p q p qa a a   ，且 2 6a   ，那么 10a 等于（ ） A． 165 B． 33 C． 30 D． 21 7．过直线 y x 上的一点作圆 2 2( 5) ( 1) 2x y    的两条切线 1 2l l， ，当直线 1 2l l， 关于 y x 对 称时，它们之间的夹角为（ ） A．30 B． 45 C． 60 D．90 8．如图，动点 P 在正方体 1 1 1 1ABCD A B C D 的对角线 1BD 上．过点 P 作垂直于平面 1 1BB D D 的 直线，与正方体表面相交于 M N， ．设 BP x ，MN y ，则函数 ( )y f x 的图象大致是（ ） A B CD M NP A1 B1 C1D1 y x A． O y x B． O y x C． O y x D． O 2008 年普通高等学校招生全国统一考试 数学（理工农医类）（北京卷） 第Ⅱ卷（共 110 分） 注意事项： 1．用钢笔或圆珠笔将答案直接写在试卷上． 2．答卷前将密封线内的项目填写清楚． 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分．把答案填在题中横线上． 9．已知 2( ) 2a i i  ，其中i 是虚数单位，那么实数 a  ． 10．已知向量 a 与 b 的夹角为120 ，且 4 a b ，那么 (2 )b a b 的值为 ． 11．若 2 3 1 n x x     展开式的各项系数之和为 32，则 n  ，其展开式中的常数项 为 ．（用数字作答） 12．如图，函数 ( )f x 的图象是折线段 ABC ，其中 A B C， ， 的坐标分别为 (0 4) (2 0) (6 4)，，，，， ，则 ( (0))f f  ； 0 (1 ) (1)limx f x f x      ．（用数字作答） 13．已知函数 2( ) cosf x x x  ，对于 π π 2 2     ， 上的任意 1 2x x， ，有如下条件： ① 1 2x x ； ② 2 2 1 2x x ； ③ 1 2x x ． 其中能使 1 2( ) ( )f x f x 恒成立的条件序号是 ． 14．某校数学课外小组在坐标纸上，为学校的一块空地设计植树方案如下：第 k 棵树种植在点 ( )k k kP x y， 处，其中 1 1x  ， 1 1y  ，当 2k ≥ 时， 1 1 1 21 5 5 5 1 2 5 5 k k k k k kx x T T k ky y T T                                       ， ． ( )T a 表示非负实数 a 的整数部分，例如 (2.6) 2T  ， (0.2) 0T  ． 2 B CA y x1O 3 4 5 6 1 2 3 4 按此方案，第 6 棵树种植点的坐标应为 ；第 2008 棵树种植点的坐标应为 ． 三、解答题：本大题共 6 小题，共 80 分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共 13 分） 已知函数 2 π( ) sin 3sin sin 2f x x x x        （ 0  ）的最小正周期为 π ． （Ⅰ）求 的值； （Ⅱ）求函数 ( )f x 在区间 2π0 3      ， 上的取值范围． 16．（本小题共 14 分） 如图，在三棱锥 P ABC 中， 2AC BC  ， 90ACB   ， AP BP AB  ， PC AC ． （Ⅰ）求证： PC AB ； （Ⅱ）求二面角 B AP C  的大小； （Ⅲ）求点C 到平面 APB 的距离． 17．（本小题共 13 分） 甲、乙等五名奥运志愿者被随机地分到 A B C D， ， ， 四个不同的岗位服务，每个岗位至少有一 名志愿者． （Ⅰ）求甲、乙两人同时参加 A 岗位服务的概率； （Ⅱ）求甲、乙两人不在同一个岗位服务的概率； （Ⅲ）设随机变量 为这五名志愿者中参加 A 岗位服务的人数，求 的分布列． A C B P 18．（本小题共 13 分）已知函数 2 2( ) ( 1) x bf x x   ，求导函数 ( )f x ，并确定 ( )f x 的单调区间． 19．（本小题共 14 分） 已知菱形 ABCD 的顶点 A C， 在椭圆 2 23 4x y  上，对角线 BD 所在直线的斜率为 1． （Ⅰ）当直线 BD 过点 (01)， 时，求直线 AC 的方程； （Ⅱ）当 60ABC   时，求菱形 ABCD 面积的最大值． 20．（本小题共 13 分） 对于每项均是正整数的数列 1 2 nA a a a： ， ， ， ，定义变换 1T ， 1T 将数列 A 变换成数列 1( )T A ： 1 21 1 1nn a a a  ， ， ， ， ． 对于每项均是非负整数的数列 1 2 mB b b b： ， ， ， ，定义变换 2T ， 2T 将数列 B 各项从大到小排列， 然后去掉所有为零的项，得到数列 2 ( )T B ； 又定义 2 2 2 1 2 1 2( ) 2( 2 )m mS B b b mb b b b         ． 设 0A 是每项均为正整数的有穷数列，令 1 2 1( ( ))( 01 2 )k kA T T A k   ，，， ． （Ⅰ）如果数列 0A 为 5，3，2，写出数列 1 2A A， ； （Ⅱ）对于每项均是正整数的有穷数列 A ，证明 1( ( )) ( )S T A S A ； （Ⅲ）证明：对于任意给定的每项均为正整数的有穷数列 0A ，存在正整数 K ，当 k K≥ 时， 1( ) ( )k kS A S A  ． 2008 年普通高等学校招生全国统一考试 数学（理工农医类）（北京卷）参考答案 一、选择题（本大题共 8 小题，每小题 5 分，共 40 分） 1．D 2．A 3．B 4．D 5．B 6．C 7．C 8．B 二、填空题（本大题共 6 小题，每小题 5 分，共 30 分） 9． 1 10． 0 11．5 10 12． 2 2 13．② 14． (1 2)， (3 402)， 三、解答题（本大题共 6 小题，共 80 分） 15．（共 13 分） 解：（Ⅰ） 1 cos2 3( ) sin 22 2 xf x x   3 1 1sin 2 cos22 2 2x x    π 1sin 2 6 2x      ． 因为函数 ( )f x 的最小正周期为 π ，且 0  ， 所以 2π π2  ，解得 1  ． （Ⅱ）由（Ⅰ）得 π 1( ) sin 2 6 2f x x      ． 因为 2π0 3x≤ ≤ ， 所以 π π 7π26 6 6x ≤ ≤ ， 所以 1 πsin 2 12 6x     ≤ ≤ ， 因此 π 1 30 sin 2 6 2 2x     ≤ ≤ ，即 ( )f x 的取值范围为 30 2      ， ． 16．（共 14 分） 解法一： （Ⅰ）取 AB 中点 D ，连结 PD CD， ． AP BP ， PD AB  ． AC BC ， CD AB  ． PD CD D  ， A C BD P A C B E P AB  平面 PCD ． PC  平面 PCD ， PC AB  ． （Ⅱ） AC BC ， AP BP ， APC BPC△ ≌△ ． 又 PC AC ， PC BC  ． 又 90ACB   ，即 AC BC ，且 AC PC C ， BC  平面 PAC ． 取 AP 中点 E ．连结 BE CE， ． AB BP ， BE AP  ． EC 是 BE 在平面 PAC 内的射影， CE AP  ． BEC 是二面角 B AP C  的平面角． 在 BCE△ 中， 90BCE   ， 2BC  ， 3 62BE AB  ， 6sin 3 BCBEC BE     ． 二面角 B AP C  的大小为 6arcsin 3 ． （Ⅲ）由（Ⅰ）知 AB  平面 PCD ， 平面 APB  平面 PCD ． 过C 作CH PD ，垂足为 H ． 平面 APB  平面 PCD PD ， CH  平面 APB ． CH 的长即为点C 到平面 APB 的距离． 由（Ⅰ）知 PC AB ，又 PC AC ，且 AB AC A ， PC  平面 ABC ． CD  平面 ABC ， PC CD  ． 在 Rt PCD△ 中， 1 22CD AB  ， 3 62PD PB  ， 2 2 2PC PD CD    ． 2 3 3 PC CDCH PD    ． A C BD P H 点C 到平面 APB 的距离为 2 3 3 ． 解法二： （Ⅰ） AC BC ， AP BP ， APC BPC△ ≌△ ． 又 PC AC ， PC BC  ． AC BC C  ， PC  平面 ABC ． AB  平面 ABC ， PC AB  ． （Ⅱ）如图，以C 为原点建立空间直角坐标系 C xyz ． 则 (0 0 0) (0 2 0) (2 0 0)C A B，，， ，，， ，， ． 设 (0 0 )P t，， ． 2 2PB AB  ， 2t  ， (0 0 2)P ，， ． 取 AP 中点 E ，连结 BE CE， ． AC PC ， AB BP ， CE AP  ， BE AP ． BEC 是二面角 B AP C  的平面角． (011)E ，，， (0 1 1)EC    ， ， ， (2 1 1)EB    ， ， ， 2 3cos 32 6 EC EBBEC EC EB           ． 二面角 B AP C  的大小为 3arccos 3 ． （Ⅲ） AC BC PC  ， C 在平面 APB 内的射影为正 APB△ 的中心 H ，且CH 的长为点C 到平面 APB 的距离． 如（Ⅱ）建立空间直角坐标系 C xyz ． 2BH HE   ， 点 H 的坐标为 2 2 2 3 3 3      ，， ． A C B P z xy HE 2 3 3CH  ． 点C 到平面 APB 的距离为 2 3 3 ． 17．（共 13 分） 解：（Ⅰ）记甲、乙两人同时参加 A 岗位服务为事件 AE ，那么 3 3 2 4 5 4 1( ) 40A AP E C A   ， 即甲、乙两人同时参加 A 岗位服务的概率是 1 40 ． （Ⅱ）记甲、乙两人同时参加同一岗位服务为事件 E ，那么 4 4 2 4 5 4 1( ) 10 AP E C A   ， 所以，甲、乙两人不在同一岗位服务的概率是 9( ) 1 ( ) 10P E P E   ． （Ⅲ）随机变量 可能取的值为 1，2．事件“ 2  ”是指有两人同时参加 A 岗位服务， 则 2 3 5 3 3 4 5 4 1( 2) 4 C AP C A     ． 所以 3( 1) 1 ( 2) 4P P      ， 的分布列是  1 3 P 3 4 1 4 18．（共 13 分） 解： 2 4 2( 1) (2 ) 2( 1)( ) ( 1) x x b xf x x        3 2 2 2 ( 1) x b x     3 2[ ( 1)] ( 1) x b x     ． 令 ( ) 0f x  ，得 1x b  ． 当 1 1b   ，即 2b  时， ( )f x 的变化情况如下表： x ( 1)b ， 1b  ( 11)b  ， (1 ) ， ( )f x  0   当 1 1b   ，即 2b  时， ( )f x 的变化情况如下表： x ( 1)， (1 1)b ， 1b  ( 1 )b   ， ( )f x   0  所以，当 2b  时，函数 ( )f x 在 ( 1)b ， 上单调递减，在 ( 11)b  ， 上单调递增， 在 (1 ) ， 上单调递减． 当 2b  时，函数 ( )f x 在 ( 1)， 上单调递减，在 (1 1)b ， 上单调递增，在 ( 1 )b   ， 上单调递 减． 当 1 1b   ，即 2b  时， 2( ) 1f x x   ，所以函数 ( )f x 在 ( 1)， 上单调递减，在 (1 ) ， 上单 调递减． 19．（共 14 分） 解：（Ⅰ）由题意得直线 BD 的方程为 1y x  ． 因为四边形 ABCD 为菱形，所以 AC BD ． 于是可设直线 AC 的方程为 y x n   ． 由 2 23 4x y y x n        ，得 2 24 6 3 4 0x nx n    ． 因为 A C， 在椭圆上， 所以 212 64 0n     ，解得 4 3 4 3 3 3n   ． 设 A C， 两点坐标分别为 1 1 2 2( ) ( )x y x y， ， ， ， 则 1 2 3 2 nx x  ， 2 1 2 3 4 4 nx x  ， 1 1y x n   ， 2 2y x n   ． 所以 1 2 2 ny y  ． 所以 AC 的中点坐标为 3 4 4 n n     ， ． 由四边形 ABCD 为菱形可知，点 3 4 4 n n     ， 在直线 1y x  上， 所以 3 14 4 n n  ，解得 2n   ． 所以直线 AC 的方程为 2y x   ，即 2 0x y   ． （Ⅱ）因为四边形 ABCD 为菱形，且 60ABC   ， 所以 AB BC CA  ． 所以菱形 ABCD 的面积 23 2S AC ． 由（Ⅰ）可得 2 2 2 2 1 2 1 2 3 16( ) ( ) 2 nAC x x y y       ， 所以 23 4 3 4 3( 3 16)4 3 3S n n           ． 所以当 0n  时，菱形 ABCD 的面积取得最大值 4 3 ． 20．（共 13 分） （Ⅰ）解： 0 5 3 2A：，，， 1 0( ) 3 4 21T A ：，，，， 1 2 1 0( ( )) 4 3 21A T T A ：，，，； 1 1( ) 4 3 21 0T A ：，，，，， 2 2 1 1( ( )) 4 3 21A T T A ：，，，． （Ⅱ）证明：设每项均是正整数的有穷数列 A 为 1 2 na a a， ， ， ， 则 1( )T A 为 n ， 1 1a  ， 2 1a  ，， 1na  ， 从而 1 1 2( ( )) 2[ 2( 1) 3( 1) ( 1)( 1)]nS T A n a a n a         2 2 2 2 1 2( 1) ( 1) ( 1)nn a a a        ． 又 2 2 2 1 2 1 2( ) 2( 2 )n nS A a a na a a a         ， 所以 1( ( )) ( )S T A S A 1 22[ 2 3 ( 1)] 2( )nn n a a a           2 1 22( )nn a a a n      2( 1) 0n n n n      ， 故 1( ( )) ( )S T A S A ． （Ⅲ）证明：设 A 是每项均为非负整数的数列 1 2 na a a， ， ， ． 当存在1 i j n≤ ≤ ，使得 i ja a≤ 时，交换数列 A 的第i 项与第 j 项得到数列 B ， 则 ( ) ( ) 2( )j i i jS B S A ia ja ia ja     2( )( ) 0j ii j a a   ≤ ． 当存在1 m n≤ ，使得 1 2 0m m na a a     时，若记数列 1 2 ma a a， ， ， 为C ， 则 ( ) ( )S C S A ． 所以 2( ( )) ( )S T A S A≤ ． 从而对于任意给定的数列 0A ，由 1 2 1( ( ))( 01 2 )k kA T T A k   ，，， 可知 1 1( ) ( ( ))k kS A S T A ≤ ． 又由（Ⅱ）可知 1( ( )) ( )k kS T A S A ，所以 1( ) ( )k kS A S A ≤ ． 即对于 k N ，要么有 1( ) ( )k kS A S A  ，要么有 1( ) ( ) 1k kS A S A ≤ ． 因为 ( )kS A 是大于 2 的整数，所以经过有限步后，必有 1 2( ) ( ) ( )k k kS A S A S A    ． 即存在正整数 K ，当 k K≥ 时， 1( ) ( )k kS A S A  ．