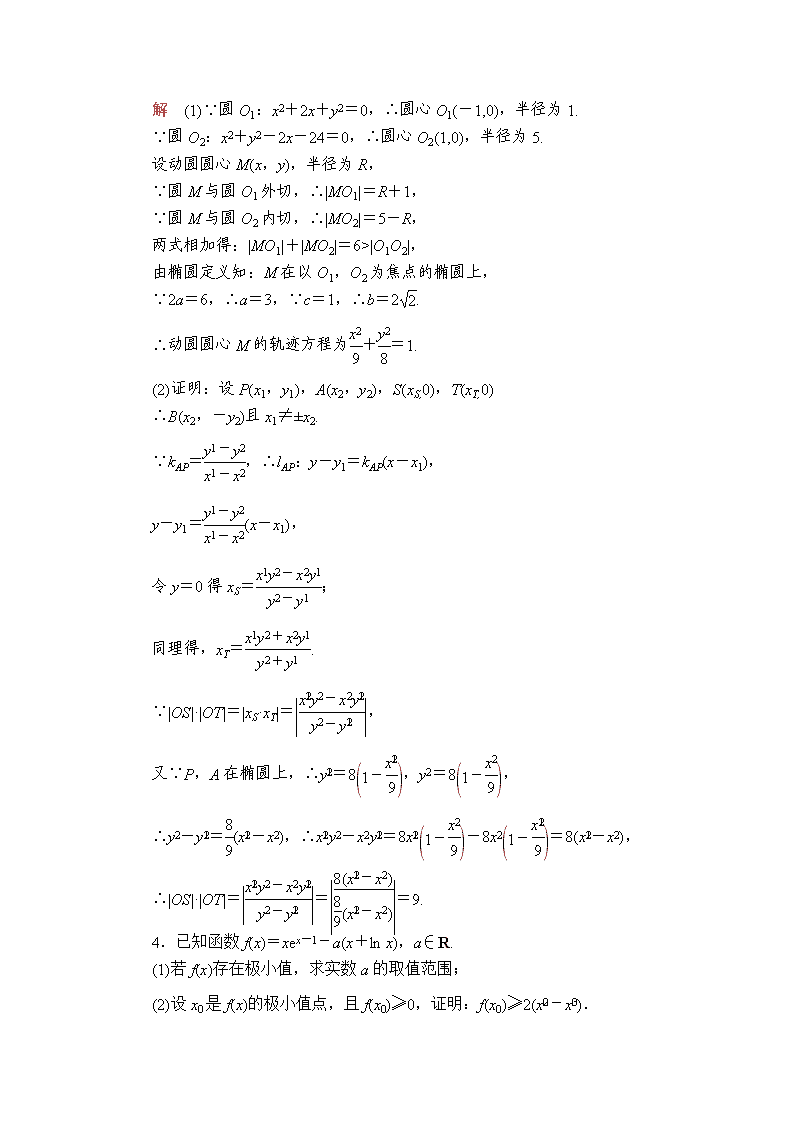高考数学二轮复习教案：高难拉分攻坚特训(二) 4页

高难拉分攻坚特训(二)‎ ‎1．已知数列{an}满足a1>0，a11＝4，an＋1＝an＋a，数列{bn}满足bn>0，b1＝a12，bn＝bn＋1＋b，n∈N*.若存在正整数m，n(m≤n)，使得bm＋bn＝14，则(　　)‎ A．m＝10，n＝12 B．m＝9，n＝11‎ C．m＝4，n＝6 D．m＝1，n＝3‎ 答案　D 解析　因为an＋1＝an＋a，bn＝bn＋1＋b，则有an＋1>an>…>a1>0，b1>b2>…>bn>0，且函数y＝x2＋x在(0，＋∞)上单调递增，故有b1＝a12＝b2＋b＝a11＋a，得b2＝a11＝4，同理有b3＝a10＝2，…，bm＝a13－m，又因为a12＝a11＋a＝12，故bm＋bn＝a10＋a12，所以m＝1，n＝3.故选D.‎ ‎2．已知f(x)＝＋b，g(x)＝[f(x)]2－1，其中a≠0，c>0，则下列判断正确的是________．(写出所有正确结论的序号)‎ ‎①f(x)的图象关于点(0，b)成中心对称；‎ ‎②f(x)在(0，＋∞)上单调递增；‎ ‎③存在M >0，使|f(x)|≤M；‎ ‎④若g(x)有零点，则b＝0；‎ ‎⑤g(x)＝0的解集可能为{1，－1,2，－2}．‎ 答案　①③⑤‎ 解析　令y＝(a≠0)，则该函数的定义域为R，且函数为奇函数，故其图象关于原点(0,0)对称．又函数y＝f(x)的图象是由y＝(a≠0)的图象向上或向下平移|b|个单位而得到的，所以函数y＝f(x)图象的对称中心为(0，b)，故①正确．‎ 当x>0时，y＝＝，若a>0，c>0，则函数y＝x＋在(0，)上单调递减，所以函数y＝f(x)单调递增；函数y＝x＋在(，＋∞)上单调递增，所以函数y＝f(x)单调递减，故②不正确．‎ 令y＝(a≠0)，则当x＝0时，y＝0，f(x)＝b，|f(x)|＝|b|，令M＝|b|＋1>0，则|f(x)|≤M成立；当x≠0时，y＝＝，则|y|＝≤＝.所以|f(x)|＝≤＋|b|≤＋|b|，令M＝＋|b|，则|f(x)|≤M成立，故③正确．‎ 若g(x)有零点，则g(x)＝[f(x)]2－1＝0，得f(x)＝±1，从而得＋b＝±1，故＝－b±1，结合③可得当g(x)有零点时，只需|－b±1|≤即可，而b不一定为零，故④不正确．‎ 由g(x)＝[f(x)]2－1＝0，得f(x)＝＋b＝±1.取b＝0，＝1，整理得x2－ax＋c＝0.当a＝3，c＝2时，方程x2－3x＋2＝0的两根为x＝1或x＝2.又函数y＝为奇函数，故方程的解集为{1，－1,2，－2}，故⑤正确．‎ 综上可得①③⑤正确．‎ ‎3．在直角坐标系xOy中，动圆M与圆O1：x2＋2x＋y2＝0外切，同时与圆O2：x2＋y2－2x－24＝0内切．‎ ‎(1)求动圆圆心M的轨迹方程；‎ ‎(2)设动圆圆心M的轨迹为曲线C，设A，P是曲线C上两点，点A关于x轴的对称点为B(异于点P)，若直线AP，BP分别交x轴于点S，T，证明：|OS|·|OT|为定值．‎ 解　(1)∵圆O1：x2＋2x＋y2＝0，∴圆心O1(－1,0)，半径为1.‎ ‎∵圆O2：x2＋y2－2x－24＝0，∴圆心O2(1,0)，半径为5.‎ 设动圆圆心M(x，y)，半径为R，‎ ‎∵圆M与圆O1外切，∴|MO1|＝R＋1，‎ ‎∵圆M与圆O2内切，∴|MO2|＝5－R，‎ 两式相加得：|MO1|＋|MO2|＝6>|O1O2|，‎ 由椭圆定义知：M在以O1，O2为焦点的椭圆上，‎ ‎∵2a＝6，∴a＝3，∵c＝1，∴b＝2.‎ ‎∴动圆圆心M的轨迹方程为＋＝1.‎ ‎(2)证明：设P(x1，y1)，A(x2，y2)，S(xS,0)，T(xT,0)‎ ‎∴B(x2，－y2)且x1≠±x2.‎ ‎∵kAP＝，∴lAP：y－y1＝kAP(x－x1)，‎ y－y1＝(x－x1)，‎ 令y＝0得xS＝；‎ 同理得，xT＝.‎ ‎∵|OS|·|OT|＝|xS·xT|＝，‎ 又∵P，A在椭圆上，∴y＝8，y＝8，‎ ‎∴y－y＝(x－x)，∴xy－xy＝8x－8x＝8(x－x)，‎ ‎∴|OS|·|OT|＝＝＝9.‎ ‎4．已知函数f(x)＝xex－1－a(x＋ln x)，a∈R.‎ ‎(1)若f(x)存在极小值，求实数a的取值范围；‎ ‎(2)设x0是f(x)的极小值点，且f(x0)≥0，证明：f(x0)≥2(x－x)．‎ 解　(1)f′(x)＝(xex－1－a)(x>0)．‎ 令g(x)＝xex－1－a，则g′(x)＝(x＋1)ex－1>0，‎ 所以g(x)在(0，＋∞)上是增函数．‎ 又因为当x→0时，g(x)→－a；‎ 当x→＋∞时，g(x)→＋∞.‎ 所以，当a≤0时，g(x)>0，f′(x)>0，函数f(x)在区间(0，＋∞)上是增函数，不存在极值点；‎ 当a>0时，g(x)的值域为(－a，＋∞)，必存在x0>0使g(x0)＝0.‎ 所以当x∈(0，x0)时，g(x)<0，f′(x)<0，f(x)单调递减；‎ 当x∈(x0，＋∞)时，g(x)>0，f′(x)>0，f(x)单调递增；‎ 所以f(x)存在极小值点．‎ 综上可知，实数a的取值范围是(0，＋∞)．‎