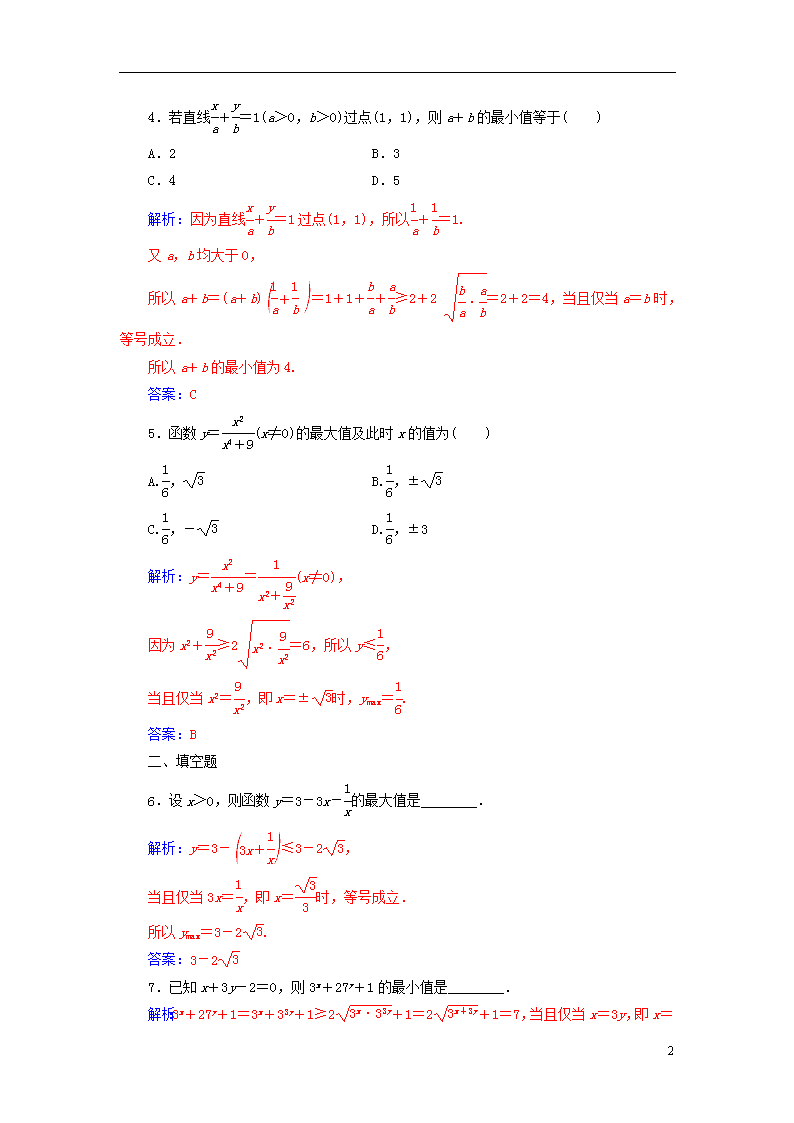2020年高中数学 第一讲基本不等式 4页

1 1.1.2 基本不等式 A 级　基础巩固 一、选择题 1．已知 a，b∈R，且 ab ≠0，则下列结论恒成立的是(　　) A．a＋b≥2 ab　　　 B. a b＋ b a≥2 C.|a b＋ b a |≥2 D．a2＋b2＞2ab 解析：当 a，b 都是负数时，A 不成立； 当 a，b 一正一负时，B 不成立； 当 a＝b 时，D 不成立，因此只有 C 是正确的． 答案：C 2．下列各式中，最小值等于 2 的是(　　) A. x y＋ y x B. x2＋5 x2＋4 C．tan θ＋ 1 tan θ D．2x＋2－x 解析：因为 2x＞0，2－x＞0， 所以 2x＋2－x≥2 2x2－x＝2. 当且仅当 2x＝2－x，即 x＝0 时，等号成立． 答案：D 3．已知 5 x＋ 3 y＝1(x＞0，y＞0)，则 xy 的最小值是(　　) A．15 B．6 C．60 D．1 解析：因为 5 x＋ 3 y≥2 15 xy(当且仅当 x＝10，y＝6 时，取等号)， 所以 2 15 xy≤1，所以 xy≥60， 故 xy 的最小值为 60. 答案：C 4．若直线 x a＋ y b＝1(a＞0，b＞0)过点(1，1)，则 a＋b 的最小值等于(　　) 2 A．2 B．3 C．4 D．5 解析：因为直线 x a＋ y b＝1 过点(1，1)，所以 1 a＋ 1 b＝1. 又 a，b 均大于 0， 所以 a＋b＝(a＋b)(1 a＋ 1 b )＝1＋1＋ b a＋ a b≥2＋2 b a· a b＝2＋2＝4，当且仅当 a＝b 时， 等号成立． 所以 a＋b 的最小值为 4. 答案：C 5．函数 y＝ x2 x4＋9(x≠0)的最大值及此时 x 的值为(　　) A. 1 6， 3 B. 1 6，± 3 C. 1 6，－ 3 D. 1 6，±3 解析：y＝ x2 x4＋9＝ 1 x2＋ 9 x2 (x≠0)， 因为 x2＋ 9 x2≥2 x2· 9 x2＝6，所以 y≤ 1 6， 当且仅当 x2＝ 9 x2，即 x＝± 3时，ymax＝ 1 6. 答案：B 二、填空题 6．设 x＞0，则函数 y＝3－3x－ 1 x的最大值是________． 解析：y＝3－(3x＋ 1 x)≤3－2 3， 当且仅当 3x＝ 1 x，即 x＝ 3 3 时，等号成立． 所以 ymax＝3－2 3. 答案：3－2 3 7．已知 x＋3y－2＝0，则 3x＋27y＋1 的最小值是________． 解析：3x＋27y＋1＝3x＋33y＋1≥2 3x·33y＋1＝2 3x＋3y＋1＝7，当且仅当 x＝3y，即 x＝1，y＝ 1 3时，等号成立． 答案：7 3 8．已知 lg x＋lg y＝2，则 1 x＋ 1 y的最小值为________． 解析：因为 lg x＋lg y＝2， 所以 x＞0，y＞0，lg(xy)＝2，所以 xy＝102， 所以 1 x＋ 1 y≥2 1 xy＝ 1 5，当且仅当 x＝y＝10 时，等号成立． 答案： 1 5 三、解答题 9．已知 x＜0，求 2x＋ 1 x的最大值． 解：由 x＜0，得－x＞0， 得－2x＋ 1 －x≥2 （－2x）( 1 －x )＝2 2， 所以 2x＋ 1 x≤－2 2， 当且仅当－2x＝ 1 －x， 即 x＝－ 2 2 时等号成立． 故 2x＋ 1 x取得最大值－2 2. 10．若 a、b、c 是不全相等的正数，求证：lg a＋b 2 ＋lg b＋c 2 ＋lg c＋a 2 ＞lg a＋lg b＋ lg c. 证明：因为 a＞0，b＞0，c＞0， 所以 a＋b 2 ≥ ab＞0， b＋c 2 ≥ bc＞0， c＋a 2 ≥ ac＞0. 且上述三个不等式中等号不能同时成立． 所以 a＋b 2 · b＋c 2 · c＋a 2 ＞abc. 所以 lg a＋b 2 ＋lg b＋c 2 ＋lg c＋a 2 ＞lg a＋lg b＋lg c. B 级　能力提升 1．某公司租地建仓库，每月土地占用费 y1 与仓库到车站的距离成反比，而每月库存货 物的运费 y2 与仓库到车站的距离成正比，如果在距离车站 10 千米处建仓库，这两项费用 y1 和 y2 分别为 2 万元和 8 万元，那么要使这两项费用之和最小，仓库应建在离车站(　　) A．5 千米处 B．4 千米处 C．3 千米处 D．2 千米处 4 解析：由已知：y1＝ 20 x ，y2＝0.8x(x 为仓库到车站的距离)． 费用之和 y＝y1＋y2＝0.8x＋ 20 x ≥2 0.8x· 20 x ＝8. 当且仅当 0.8x＝ 20 x ，即 x＝5 时等号成立． 答案：A 2．(2017·天津卷)若 a，b∈R，ab＞0，则 a4＋4b4＋1 ab 的最小值为________． 解析：因为 a，b∈R，ab＞0， 所以 a4＋4b4＋1 ab ≥ 4a2b2＋1 ab ＝4ab＋ 1 ab≥2 4ab· 1 ab＝4， 当且仅当{a2＝2b2， 4ab＝ 1 ab，即{a2＝ 2 2 ， b2＝ 2 4 时取得等号． 故 a4＋4b4＋1 ab 的最小值为 4. 答案：4 3．若对任意 x＞0， x x2＋3x＋1≤a 恒成立，求实数 a 的取值范围． 解：由 x＞0，知原不等式等价于 0＜ 1 a≤ x2＋3x＋1 x ＝x＋ 1 x＋3 恒成立． 又 x＞0 时，x＋ 1 x≥2 x· 1 x＝2， 所以 x＋ 1 x＋3≥5，当且仅当 x＝1 时，取等号． 因此(x＋ 1 x＋3) min＝5， 从而 0＜ 1 a≤5，解得 a≥ 1 5. 故实数 a 的取值范围为[1 5，＋∞).