2020高中数学 第二章 函数概念与基本初等函数I 2 7页

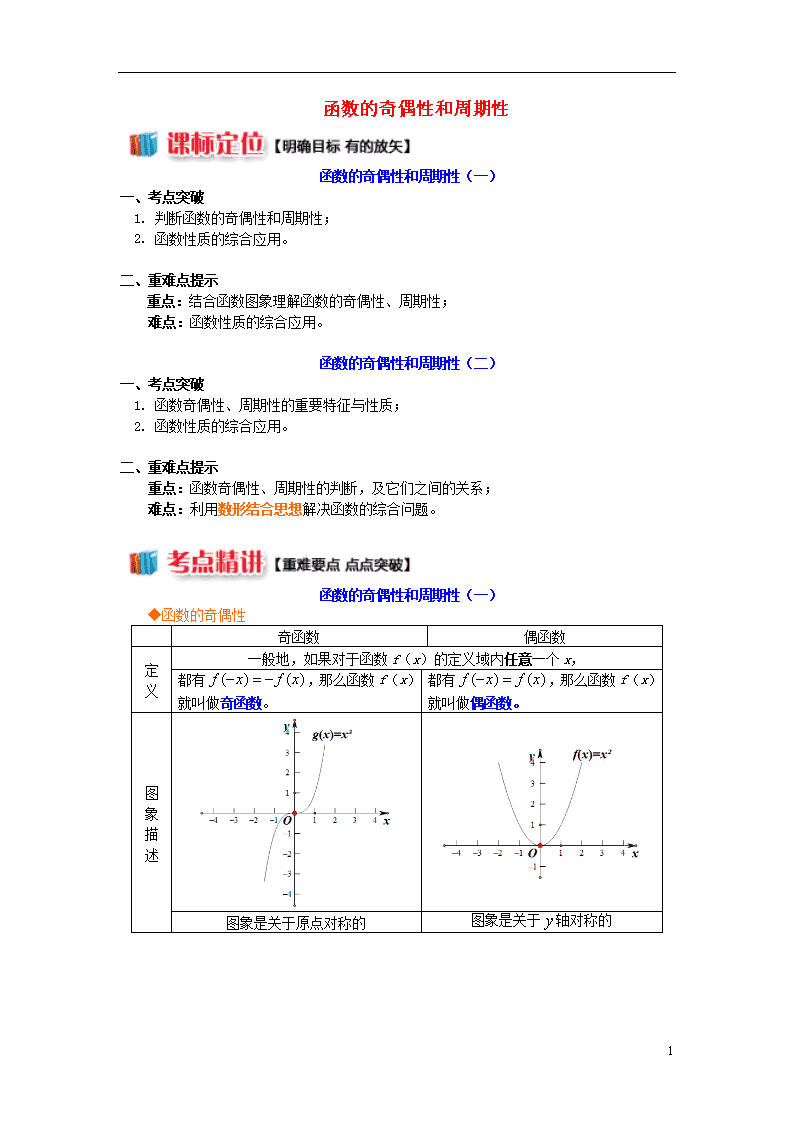
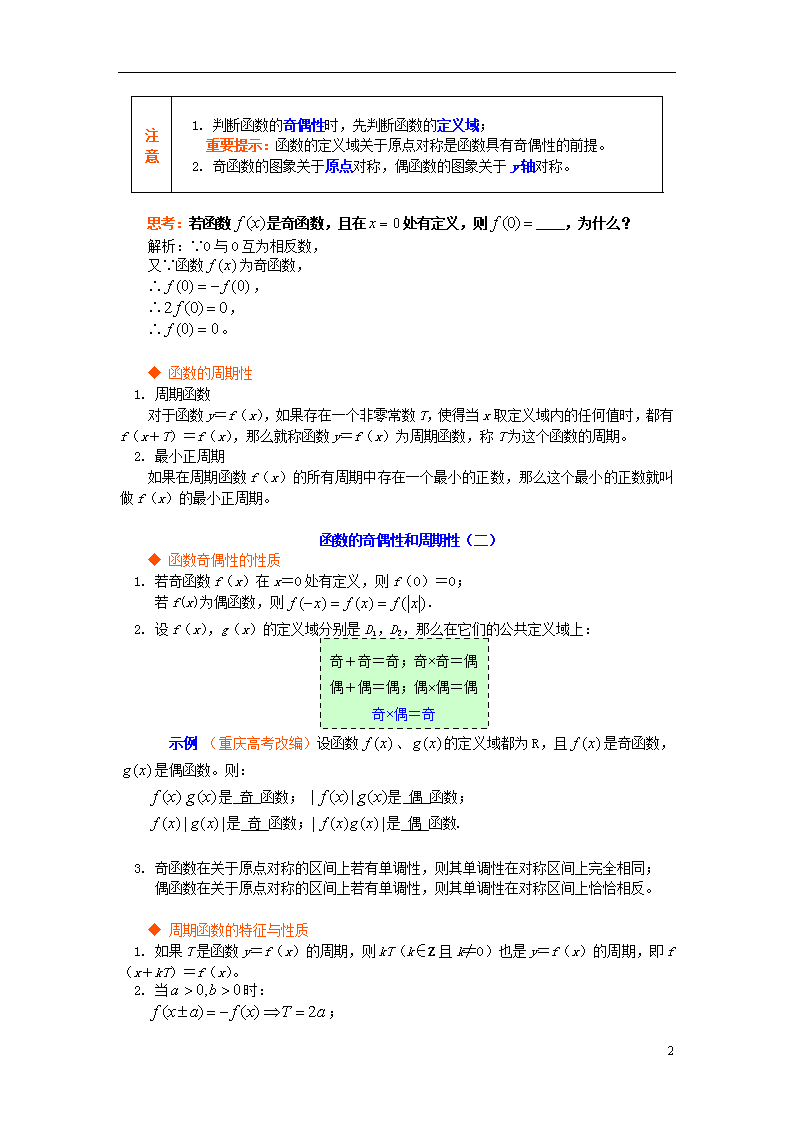
函数的奇偶性和周期性 函数的奇偶性和周期性（一）‎ 一、考点突破 ‎1. 判断函数的奇偶性和周期性；‎ ‎2. 函数性质的综合应用。‎ 二、重难点提示 重点：结合函数图象理解函数的奇偶性、周期性；‎ 难点：函数性质的综合应用。‎ 函数的奇偶性和周期性（二）‎ 一、考点突破 ‎1. 函数奇偶性、周期性的重要特征与性质；‎ ‎2. 函数性质的综合应用。‎ 二、重难点提示 重点：函数奇偶性、周期性的判断，及它们之间的关系；‎ 难点：利用数形结合思想解决函数的综合问题。‎ 函数的奇偶性和周期性（一）‎ ‎◆函数的奇偶性 奇函数 偶函数 定义 一般地，如果对于函数f（x）的定义域内任意一个x，‎ 都有，那么函数f（x）就叫做奇函数。‎ 都有，那么函数f（x）就叫做偶函数。‎ 图象 描述 图象是关于原点对称的 图象是关于轴对称的 7‎ 注意 ‎1. 判断函数的奇偶性时，先判断函数的定义域；‎ 重要提示：函数的定义域关于原点对称是函数具有奇偶性的前提。‎ ‎2. 奇函数的图象关于原点对称，偶函数的图象关于y轴对称。‎ 思考：若函数是奇函数，且在处有定义，则____，为什么？‎ 解析：∵0与0互为相反数，‎ 又∵函数为奇函数，‎ ‎∴，‎ ‎∴，‎ ‎∴。‎ ‎◆ 函数的周期性 ‎1. 周期函数 对于函数y＝f（x），如果存在一个非零常数T，使得当x取定义域内的任何值时，都有f（x＋T）＝f（x），那么就称函数y＝f（x）为周期函数，称T为这个函数的周期。‎ ‎2. 最小正周期 如果在周期函数f（x）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f（x）的最小正周期。‎ 函数的奇偶性和周期性（二）‎ ‎◆ 函数奇偶性的性质 ‎1. 若奇函数f（x）在x＝0处有定义，则f（0）＝0；‎ 若f(x)为偶函数，则.‎ ‎2. 设f（x），g（x）的定义域分别是D1，D2，那么在它们的公共定义域上：‎ 奇＋奇＝奇；奇×奇＝偶 偶＋偶＝偶；偶×偶＝偶 奇×偶＝奇 示例 （重庆高考改编）设函数、的定义域都为R，且是奇函数，是偶函数。则：‎ 是 奇 函数； 是 偶 函数；‎ 是 奇 函数；是 偶 函数.‎ ‎3. 奇函数在关于原点对称的区间上若有单调性，则其单调性在对称区间上完全相同；‎ 偶函数在关于原点对称的区间上若有单调性，则其单调性在对称区间上恰恰相反。‎ ‎◆ 周期函数的特征与性质 ‎1. 如果T是函数y＝f（x）的周期，则kT（k∈Z且k≠0）也是y＝f（x）的周期，即f（x＋kT）＝f（x）。‎ ‎2. 当时：‎ ‎；‎ 7‎ ‎；‎ ‎。‎ 函数的奇偶性和周期性（一）‎ 例题1 判断下列函数的奇偶性：‎ ‎（1）f（x）＝＋；‎ ‎（2）f（x）＝（x＋1） .‎ 思路分析：确定函数的奇偶性时，必须先判定函数定义域是否关于原点对称。若对称，再验证f（－x）＝±f（x）或其等价形式f（－x）±f（x）＝0是否成立。‎ 答案：解：（1）由，得x＝±3。‎ ‎∴f（x）的定义域为{－3，3}。‎ 又f（3）＋f（－3）＝0，f（3）－f（－3）＝0。‎ 即f（x）＝±f（－x）。‎ ‎∴f（x）既是奇函数，又是偶函数。‎ ‎（2）由，得。‎ ‎∵f（x）的定义域（－1，1]不关于原点对称。‎ ‎∴f（x）既不是奇函数，也不是偶函数。‎ 技巧点拨：判断函数的奇偶性，其中包括两个必备条件：‎ ‎（1）定义域关于原点对称。这是函数具有奇偶性的必要不充分条件，所以首先考虑定义域对解决问题是有利的；‎ ‎（2）判断f（x）与f（－x）是否具有等量关系。在判断奇偶性的运算中，可以转化为判断奇偶性的等价等量关系式（f（x）＋f（－x）＝0（奇函数）或f（x）－f（－x）＝0（偶函数）是否成立。‎ 例题2 设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x＋2）＝－f（x）。当x∈[0，2]时，f（x）＝2x－x2。‎ ‎（1）求证：f（x）是周期函数；‎ ‎（2）当x∈[2，4]时，求f（x）的解析式。‎ 思路分析：（1）只须证明f（x＋T）＝f（x），即可说明f（x）是周期函数；‎ ‎（2）由f（x）在[0，2]上的解析式求得f（x）在[－2，0]上的解析式，进而求f（x）在[2，4]上的解析式。‎ 答案：（1）证明：∵f（x＋2）＝－f（x），‎ ‎∴f（x＋4）＝－f（x＋2）＝f（x）。‎ ‎∴f（x）是周期为4的周期函数。‎ ‎（2）解：∵x∈[2，4]，∴－x∈[－4，－2]，‎ ‎∴4－x∈[0，2]，‎ 7‎ 又∵当时，，‎ ‎∴f（4－x）＝2（4－x）－（4－x）2＝－x2＋6x－8，‎ 又f（4－x）＝f（－x）＝－f（x），‎ ‎∴－f（x）＝－x2＋6x－8，‎ 即f（x）＝x2－6x＋8，x∈[2，4]。‎ 技巧点拨：对于周期函数在特定区间上的二次函数的求法，要善于转化区间，利用已知区间上的函数的解析式来求未知区间上的二次函数的解析式。‎ 函数的奇偶性和周期性（二）‎ 例题1 设是定义在上的偶函数，其图象关于直线对称，对任意的，，都有.‎ （1） 设，求，；‎ （2） 证明是周期函数。‎ 思路分析：‎ ‎（1）灵活赋值，令代入到，可求得的值；‎ 令代入到可求得的值。‎ ‎（2）灵活利用函数的奇偶性和图象关于直线对称，将文字语言转化为数学语言。‎ 答案：‎ ‎（1）解: 令代入到中，‎ 得：，∴或 令代入到，‎ 得：，∴，或，‎ 同理可得，∴‎ ‎（2）证明：∵的图象关于直线对称，‎ ‎∴ ①‎ 又∵是定义在上的偶函数，‎ 7‎ ‎∴，∴ ②‎ 由①②两式可得：，‎ ‎∴，‎ ‎∴是周期为2的周期函数.‎ 技巧点拨：本题考查函数奇偶性与周期性以及抽象函数的综合，根据题目已知条件进行灵活赋值来求函数值，灵活利用函数奇偶性和关于直线的对称性来导出函数的周期性。‎ 例题2 已知f（x）是定义在R上的偶函数，并且f（x＋2）=－，当2≤x≤3时，‎ f（x）＝x，则f（105.5）＝________。‎ 思路分析：将形如f（x＋2）＝－式子进行变形是解题的关键。这里的几种变形方法一定要理解并掌握。‎ 答案：由已知，可得f（x＋4）＝f[（x＋2）＋2]‎ ‎＝－＝－＝f（x）。‎ 故函数的周期为4。‎ ‎∴f（105.5）＝f（4×27－2.5）＝f（－2.5）。‎ ‎∵2≤2.5≤3，由题意，得f（2.5）＝2.5。‎ ‎∴f（105.5）＝2.5。‎ 技巧点拨：对周期函数的特征要熟悉，并且要熟练掌握数形结合、转化与化归等思想。‎ 函数的奇偶性和周期性（一）‎ 巧用函数性质进行等价转换 示例 函数f（x）的定义域D＝{x|x≠0}，且满足对于任意x1，x2∈D，有f（x1·x2）＝f（x1）＋f（x2）。‎ ‎（1）求f（1）的值；‎ ‎（2）判断f（x）的奇偶性并证明；‎ ‎（3）如果f（4）＝1，f（3x＋1）＋f（2x－6）≤3，且f（x）在（0，＋∞）上是增函数，求x的取值范围。‎ 思路分析：（1）从f（1）联想自变量的值为1，进而想到赋值x1＝x2＝1。‎ ‎（2）判断f（x）的奇偶性，就是研究f（x）、f（－x）的关系。从而想到赋值x1＝－1，x2＝x，即f（－x）＝f（－1）＋f（x）。‎ ‎（3）将函数不等式转化为f（M）N的形式求解。‎ 答案：解：（1）令x1＝x2＝1，‎ 有f（1×1）＝f（1）＋f（1），解得f（1）＝0.‎ 7‎ ‎（2）f（x）为偶函数，证明如下：‎ 令x1＝x2＝－1，‎ 有f[（－1）×（－1）]＝f（－1）＋f（－1），解得f（－1）＝0。‎ 令x1＝－1，x2＝x，有f（－x）＝f（－1）＋f（x），‎ ‎∴f（－x）＝f（x）。∴f（x）为偶函数。‎ ‎（3）f（4×4）＝f（4）＋f（4）＝2，‎ f（16×4）＝f（16）＋f（4）＝3。‎ 由f（3x＋1）＋f（2x－6）≤3，‎ 变形为f[（3x＋1）（2x－6）]≤f（64）。（*）‎ ‎∵f（x）为偶函数，∴f（－x）＝f（x）＝f（|x|）。‎ ‎∴不等式（*）等价于f[|（3x＋1）（2x－6）|]≤f（64）。‎ 又∵f（x）在（0，＋∞）上是增函数，‎ ‎∴|（3x＋1）（2x－6）|≤64，且（3x＋1）（2x－6）≠0.‎ 解得－≤x<－或－