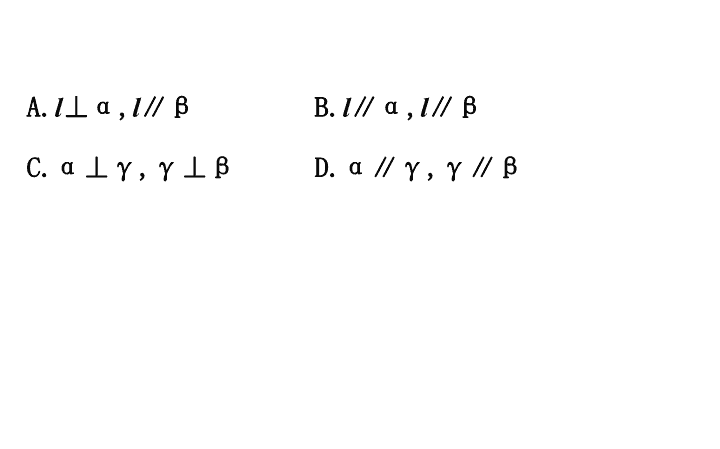2020届高考文科数学二轮专题复习课件：专题4 立体几何2-4-高考小题 2 30页

第 2 课时　 空间点、线、面的位置关系 考向一　线面位置关系的判断 ( 保分题型考点 ) 【题组通关 】 1. 已知直线 l , 平面 α,β,γ , 则下列能推出 α∥β 的条件是 ( 　　 ) A. l ⊥α, l ∥β B. l ∥α, l ∥β C.α⊥γ,γ⊥β D.α∥γ,γ∥β 2. 若空间中四条两两不同的直线 l 1 , l 2 , l 3 , l 4 , 满足 l 1 ⊥ l 2 , l 2 ⊥ l 3 , l 3 ⊥ l 4 , 则下列结论一定正确的是 ( 　　 ) 世纪金榜导学号 A. l 1 ⊥ l 4 B. l 1 ∥ l 4 C. l 1 与 l 4 既不垂直也不平行 D. l 1 与 l 4 的位置关系不确定 【题型建模 】 1. 判断面面平行 : 根据空间中平行与垂直的判定及性质定理进行分析 2. 正方体模型法 : 作出正方体模型 数形结合法求解 【解析 】 1. 选 D.A 项 , l ⊥α, l ∥β⇒α⊥β , 故 A 错 ;B 项 , 平面 α,β 还可能相交 , 故 B 错 ;C 项 , 平面 α,β 还可能相交 , 故 C 错 ; 由面面平行的传递性知 ,D 项正确 . 2. 选 D. 不妨令 l 1 , l 2 , l 3 分别为如图所示正方体的边所在直线 . 若 l 4 为直线 B 1 C 1 , 则有 l 1 ∥ l 4 ; 若 l 4 为直线 C 1 D 1 , 则 l 1 ⊥ l 4 ; 若 l 4 为直线 A 1 C 1 , 则 l 1 与 l 4 异面 , 故 l 1 与 l 4 的位置关系不确定 . 【拓展提升 】 点、线、面的位置关系的判断方法 (1) 平面的基本性质是立体几何的基本理论基础 , 也是判断线面关系的基础 . 对点、线、面的位置关系的判断 , 常采用穷举法 , 即对各种关系都进行考虑 , 要充分发挥模型的直观性作用 . (2) 利用线线平行、线面平行、面面平行以及线线垂直、线面垂直、面面垂直的判定定理、性质定理综合进行推理和判断命题是否正确 . 【变式训练 】 (2019 · 日照联考 ) 已知 m,n 是两条不同直线 ,α,β 是两个不同平面 , 给出四个命题 : ① 若 α∩β=m,n ⊂ α,n⊥m , 则 α⊥β ;② 若 m⊥α,m⊥β , 则 α∥β ;③ 若 m⊥α,n⊥β,m⊥n , 则 α⊥β ;④ 若 m∥α,n∥β,m∥n , 则 α∥β . 其中正确的命题是 ( 　　 ) A.①② B.②③ C.①④ D.②④ 【解析 】 选 B.① 若 α∩β=m,n ⊂ α,n⊥m , 如图 , 则 α 与 β 不一定垂直 , 故 ① 为假命题 ; ② 若 m⊥α,m⊥β , 根据垂直于同一条直线的两个平面平行 , 则 α∥β ; 故 ② 为真命题 ; ③ 若 m⊥α,n⊥β,m⊥n , 则 α⊥β , 故 ③ 为真命题 ; ④ 若 m∥α,n∥β,m∥n , 如图 , 则 α 与 β 可能相交 , 故 ④ 为假命题 . 考向二　异面直线所成的角 ( 保分题型考点 ) 【例 2 】 (1) 如图所示 , 四棱锥 P-ABCD 中 , ∠ABC=∠BAD=90°,BC=2AD,△PAB 和 △PAD 都是等边三角形 , 则异面直线 CD 与 PB 所成角的大小为 ________.  (2) 如图 , 在三棱柱 ABC-A 1 B 1 C 1 中 ,AC⊥BC,AC⊥CC 1 , BC⊥CC 1 ,AA 1 =4,AC=BC=2, 则异面直线 A 1 B 与 AC 所成角的正弦值是 ________. 世纪金榜导学号   【题型建模 】 (1) 求异面直线所成的角 : 作出异面直线所成的角 , 利用余弦定理求解 (2) 几何法 : 作角 证角 求角 【解析 】 (1) 如图所示 , 延长 DA 至 E, 使 AE=DA, 连接 PE,BE. 因为 ∠ ABC=∠BAD=90°,BC=2AD, 所以 DE=BC,DE∥BC. 所以四边形 CBED 为平行四边形 , 所以 CD∥BE, 所以 ∠PBE 就是异面直线 CD 与 PB 所成的角 . 在 △PAE 中 ,AE=PA,∠PAE=120°, 由余弦定理 , 得 PE= = = AE. 在 △ABE 中 ,AE=AB,∠BAE=90°, 所以 BE= AE. 因为 △PAB 是等边三角形 , 所以 PB=AB=AE, 所以 PB 2 +BE 2 =AE 2 +2AE 2 =3AE 2 =PE 2 , 所以 ∠ PBE=90°. 答案 : 90° (2) 由 AC⊥BC,AC⊥CC 1 ,BC⊥CC 1 可知三棱柱 ABC-A 1 B 1 C 1 为直三棱柱 , 连接 BC 1 , 图略 . 由于 AC∥A 1 C 1 , 所以 ∠ BA 1 C 1 ( 或其补角 ) 就是所求异面直线所成的角 . 在 △ BA 1 C 1 中 ,A 1 B=2 ,A 1 C 1 =2,BC 1 =2 , 所以 cos∠BA 1 C 1 = ,sin∠BA 1 C 1 = . 答案 : 【拓展提升 】 求异面直线所成角的方法 (1) 几何法 ① 作 : 利用定义转化为平面角 , 对于异面直线所成的角 , 可固定一条 , 平移一条 , 或两条同时平移到某个特殊的位置 , 顶点选在特殊的位置上 . ② 证 : 证明作出的角为所求角 . ③ 求 : 把这个平面角置于一个三角形中 , 通过解三角形求空间角 . 【变式训练 】 已知二面角 α- l -β 为 60°,AB⊂α,AB⊥ l ,A 为垂足 , CD⊂β,C∈ l ,∠ACD =135°, 则异面直线 AB 与 CD 所成角 的余弦值为 ( 　　 ) 　　　　　 　　　　　　 　　　　　　 A. B. C. D. 【解析 】 选 B. 如图 , 在平面 α 内过 C 作 CE∥AB, 则 ∠ECD 为异面直线 AB 与 CD 所成的角或其补角 . 不妨取 CE=1, 过 E 作 EO⊥β 于点 O. 在平面 β 内过 O 作 OH⊥CD 于点 H, 连接 EH, 则 EH⊥CD. 因为 AB∥CE,AB⊥ l , 所以 CE⊥ l . 又因为 EO⊥β , 所以 CO⊥ l . 故 ∠ECO 为二面角 α- l -β 的平面角 , 所以 ∠ ECO=60°. 而 ∠ ACD=135°,CO⊥ l , 所以 ∠ OCH=45°. 在 Rt△ECO 中 ,CO=CE·cos∠ECO =1×cos 60°= . 在 Rt△COH 中 ,CH=CO·cos∠OCH = ×sin 45°= . 在 Rt△ECH 中 ,cos∠ECH = . 所以异面直线 AB 与 CD 所成角的余弦值为 .