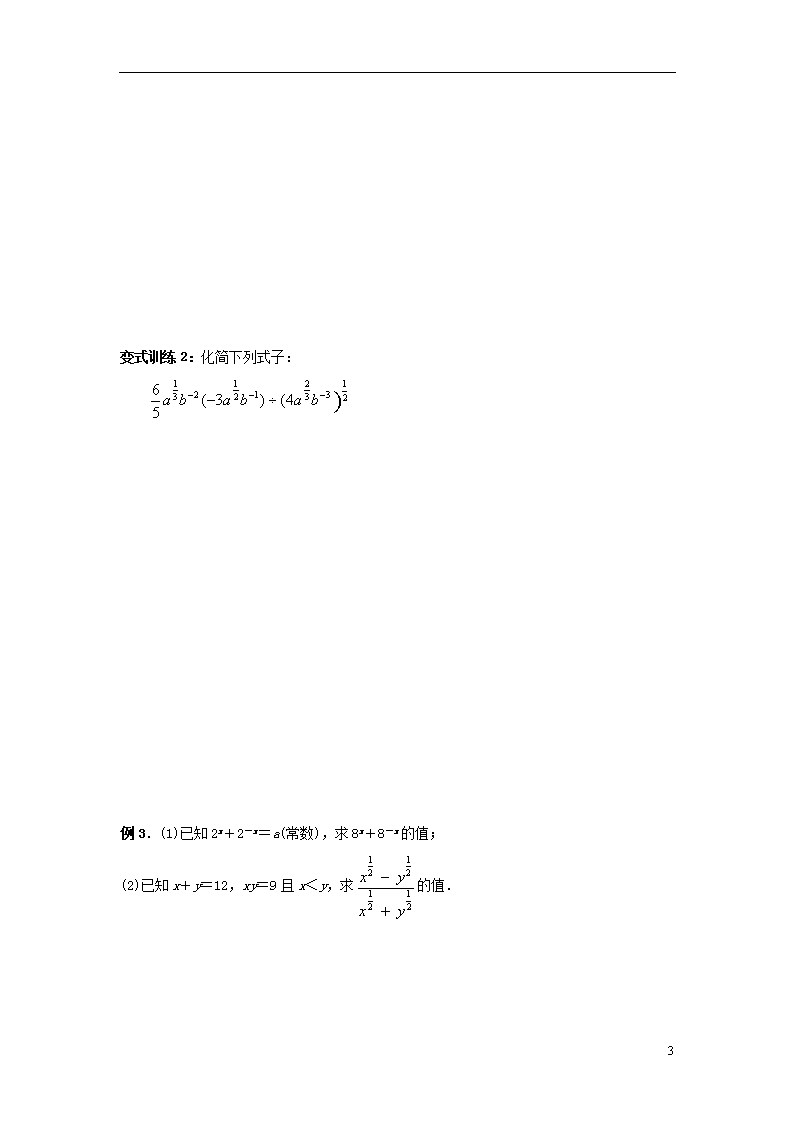2020高中数学 第二章 基本初等函数2.1.1指数与指数幂的运算（2） 4页

‎2.1.1‎指数与指数幂的运算（2）‎ ‎【导学目标】 ‎ ‎1.掌握根式与分数指数幂的互化；‎ ‎2.掌握有理数指数幂的运算性质，了解从特殊到一般的思维过程.‎ ‎【自主学习】‎ 知识回顾：方根、根式、整数指数幂等 新知梳理：‎ 导入：根据，对于根式，其被开方数的指数不能被根指数整除时，也可以写成分数指数幂的形式.‎ ‎1. 分数指数幂 ‎（1）正数的正分数指数幂的意义 ‎= ___ ，= ___ ，= ___ ；‎ 规定：= _____().‎ ‎（2）正数的负分数指数幂的意义 ‎= ____ ，= ____ ，= ____ ；‎ 规定：= __ ().‎ ‎（3）的分数指数幂 的正分数指数幂等于 _____ ，的负分数指数幂 _______ .‎ ‎（4）分数指数幂的运算性质：‎ ‎① _______ ；‎ ‎② __ ；‎ ‎③ .‎ 至此，指数的概念就从整数指数幂推广到有理数指数幂.‎ 对点练习：1. 若有意义，则的取值范围是（　　　）‎ A．Ｒ　 B．0.5　 ‎ C．＞0.5 D．＜0.5‎ ‎2. 无理指数幂的含义：如，它是一个确定的实数，可以看成由以的一串不足近似值和相应的一串过剩近似值为指数的有理数幂的值逐渐逼近的结果.‎ ‎3. 根式的运算:先把根式化成分数指数幂，然后利用 的运算性质进行运算.‎ 对点练习：‎ ‎2. 等于（ ）‎ 4‎ A、 B、 C、 D、 ‎ ‎3. 　　 ．‎ ‎【合作探究】‎ 典例精析 例题1：（1）用分数指数幂表示下列式子：‎ ‎ =________________________‎ ‎ =________________________‎ ‎（2）求值：‎ ‎ = ‎ ‎= ‎ ‎=‎ 变式训练1：化简：‎ ‎（1） ‎ ‎（2）‎ 例题2：计算下列各式（式中字母均为正数）：‎ ‎ （1）；‎ ‎（2）‎ 4‎ 变式训练2：化简下列式子：‎ 例3．(1)已知2x＋2－x＝a(常数)，求8x＋8－x的值；‎ ‎(2)已知x＋y＝12，xy＝9且x＜y，求的值．‎ 4‎ 变式训练3：若a＝2，b>0，求＋的值．‎ ‎【课堂小结】‎ 4‎