人教版高三数学总复习第二章单元质量检测 9页

第二章单元质量检测 时间：90分钟　分值：100分 一、选择题(每小题4分，共40分)‎ ‎1．函数y＝的定义域为(　　)‎ A. B.∪(－1，＋∞)‎ C. D.∪(－1，＋∞)‎ 解析：由得x∈.‎ 答案：A ‎2．曲线y＝x3－2x＋4在点(1,3)处的切线的倾斜角为(　　)‎ A．30° B．45°‎ C．60° D．120°‎ 解析：由y′＝3x2－2得y′|x＝1＝1，即曲线在点(1,3)处的切线斜率为1，所以切线的倾斜角为45°.‎ 答案：B ‎3．若已知函数f(x)＝则f(f(1))＋f 的值是(　　)‎ A．7 B．2‎ C．5 D．3‎ 解析：f(1)＝log21＝0，所以f(f(1))＝f(0)＝2.因为log3<0，所以f eq lc( c)(avs4alco1(log3f(1,2)))＝9＋1＝9log32＋1＝32log32＋1＝3log34＋1＝4＋1＝5，所以f(f(1))＋f＝2＋5＝7，故选A.‎ 答案：A ‎4．已知a＝0.7，b＝0.6，c＝log2.11.5，则a，b，c的大小关系是(　　)‎ A．c0，即f(x)在R上单调递增，因此函数f(x)只有一个零点，故选A.‎ 答案：A ‎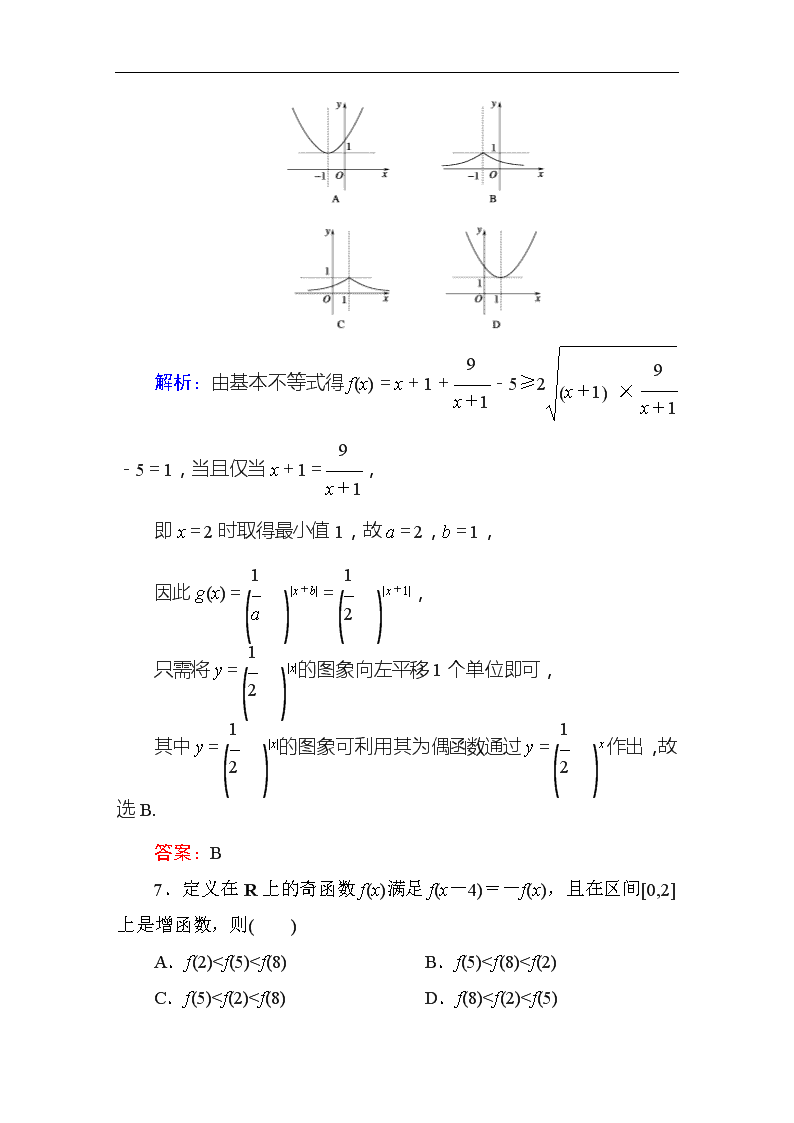6．已知函数f(x)＝x－4＋，x∈(0,4)，当x＝a时，f(x)取得最小值b，则函数g(x)＝|x＋b|的图象为(　　)‎ 解析：由基本不等式得f(x)＝x＋1＋－5≥2－5＝1，当且仅当x＋1＝，‎ 即x＝2时取得最小值1，故a＝2，b＝1，‎ 因此g(x)＝|x＋b|＝|x＋1|，‎ 只需将y＝|x|的图象向左平移1个单位即可，‎ 其中y＝|x|的图象可利用其为偶函数通过y＝x作出，故选B.‎ 答案：B ‎7．定义在R上的奇函数f(x)满足f(x－4)＝－f(x)，且在区间[0,2]上是增函数，则(　　)‎ A．f(2)0时，f(x)的单调递减区间是(－3m，m)，若f(x)在区间(－2,3)上是减函数，则，解得m≥3.当m<0时，f(x)的单调递减区间是(m，－3m)，若f(x)在区间(－2,3)上是减函数，则，解得m≤－2.综上所述，实数m的取值范围是m≥3或m≤－2.故选D.‎ 答案：D ‎9．若a>0，b>0，且函数f(x)＝4x3－ax2－2bx＋2在x＝1处有极值，则ab的最大值等于(　　)‎ A．2 B．3‎ C．6 D．9‎ 解析：∵f′(x)＝12x2－2ax－2b，‎ Δ＝4a2＋96b>0，又x＝1是极值点，‎ ‎∴f′(1)＝12－2a－2b＝0，即a＋b＝6，且a>0，b>0，‎ ‎∴ab≤＝9，当且仅当a＝b时“＝”成立，所以ab的最大值为9.‎ 答案：D ‎10．(2014·湖南卷)若0lnx2－lnx1 B．ex2－ex1x1ex2 D．x2ex1g(x2)，x2ex1>x1ex2，故选C.‎ 答案：C 二、填空题(每小题4分，共16分)‎ ‎11．设f(x)＝则f[f(－1)]＝________.‎ 解析：f(－1)＝(－1)2＝1，所以f[f(－1)]＝f(1)＝21＝2.‎ 答案：2‎ ‎12．不等式x2－2x<0表示的平面区域与抛物线y2＝4x围成的封闭区域的面积为________．‎ 解析：由x2－2x<0，得00)有实根，‎ 所以a＝－<0.‎ 答案：(－∞，0)‎ ‎14．对于函数f(x)＝x|x|＋px＋q，现给出四个命题：‎ ‎①q＝0时，f(x)为奇函数；‎ ‎②y＝f(x)的图象关于(0，q)对称；‎ ‎③p＝0，q>0时，方程f(x)＝0有且只有一个实数根；‎ ‎④方程f(x)＝0至多有两个实数根．‎ 其中正确命题的序号为________．‎ 解析：若q＝0，则f(x)＝x|x|＋px＝x(|x|＋p)为奇函数，所以①正确；由①知，当q＝0时，f(x)为奇函数，图象关于原点对称，f(x)＝x|x|＋px＋q的图象由函数f(x)＝x|x|＋px向上或向下平移|q|个单位，所以图象关于(0，q)对称，所以②正确；当p＝0，q>0时，f(x)＝x|x|＋q＝当f(x)＝0，得x＝－，只有一解，所以③正确；取q＝0，p＝－1，f(x)＝x|x|－x＝由f(x)＝0，可得x＝0，x＝±1有三个实根，所以④不正确．综上正确命题的序号为①②③.‎ 答案：①②③‎ 三、解答题(共4小题，共44分，解答应写出必要的文字说明、计算过程或证明步骤．)‎ ‎15．(10分)已知函数f(x)＝a－.‎ ‎(1)求证：函数y＝f(x)在(0，＋∞)上是增函数．‎ ‎(2)若f(x)<2x在(1，＋∞)上恒成立，求实数a的取值范围．‎ 解：(1)证明：当x∈(0，＋∞)时，f(x)＝a－，‎ 设00，x2－x1>0，‎ f(x2)－f(x1)＝－ ‎＝－＝>0，‎ 所以f(x)在(0，＋∞)上是增函数．‎ ‎(2)由题意a－<2x在(1，＋∞)上恒成立，‎ 设h(x)＝2x＋，则a1，‎ 所以2－>0，所以h(x1)0，f(x)单调递增；‎ 当x∈时，f′(x)<0，f(x)单调递减，‎ 故f(x)在x＝－2取极小值f(－2)＝0，在x＝0取极大值f(0)＝4.‎ ‎(2)f′(x)＝，‎ 因为当x∈时，<0，‎ 依题意当x∈时，有5x＋(3b－2)≤0，从而＋(3b－2)≤0.‎ 所以b的取值范围为.‎ ‎17．(12分)设函数f(x)＝x2＋ax－lnx(a∈R)．‎ ‎(1)若a＝1，求函数f(x)的单调区间；‎ ‎(2)过坐标原点O作曲线y＝f(x)的切线，证明：切点的横坐标为1.‎ 解：(1)a＝1时，f(x)＝x2＋x－lnx(x>0)，‎ ‎∴f′(x)＝2x＋1－＝，‎ 当x∈时，f′(x)<0；‎ 当x∈时，f′(x)>0.‎ ‎∴f(x)的单调递减区间为，单调递增区间为.‎ ‎(2)证明：设切点为M(t，f(t))，f′(x)＝2x＋a－，‎ 切线的斜率k＝2t＋a－，又切线过原点，则k＝，‎ ‎∴＝2t＋a－，即t2＋at－lnt＝2t2＋at－1.‎ ‎∴t2－1＋lnt＝0，‎ 存在性：t＝1满足方程t2－1＋lnt＝0，‎ ‎∴t＝1是方程t2－1＋lnt＝0的根．‎ 再证唯一性：设φ(t)＝t2－1＋lnt，φ′(t)＝2t＋>0，‎ φ(t)在(0，＋∞)单调递增，且φ(1)＝0，‎ ‎∴方程t2－1＋lnt＝0有唯一解．‎ 综上，切点的横坐标为1.‎ ‎18．(12分)(2014·新课标全国卷Ⅱ)已知函数f(x)＝x3－3x2＋ax＋2，曲线y＝f(x)在点(0,2)处的切线与x轴交点的横坐标为－2.‎ ‎(1)求a；‎ ‎(2)证明：当k<1时，曲线y＝f(x)与直线y＝kx－2只有一个交点．‎ 解：(1)f′(x)＝3x2－6x＋a，f′(0)＝a，‎ 曲线y＝f(x)在点(0,2)处的切线方程为y＝ax＋2.‎ 由题意得－＝－2，所以a＝1.‎ ‎(2)由(1)知，f(x)＝x3－3x2＋x＋2.‎ 设g(x)＝f(x)－kx＋2＝x3－3x2＋(1－k)x＋4.‎ 由题设知1－k>0.‎ 当x≤0时，g′(x)＝3x2－6x＋1－k>0，g(x)单调递增，g(－1)＝k－1<0，g(0)＝4，所以g(x)＝0在(－∞，0]有唯一实根．‎ 当x>0时，令h(x)＝x3－3x2＋4，则g(x)＝h(x)＋(1－k)x>h(x)．‎ h′(x)＝3x2－6x＝3x(x－2)，h(x)在(0,2)单调递减，在(2，＋∞)单调递增，所以g(x)>h(x)≥h(2)＝0.‎ 所以g(x)＝0在(0，＋∞)没有实根．‎ 综上，g(x)＝0在R有唯一实根，即曲线y＝f(x)与直线y＝kx－2只有一个交点．‎