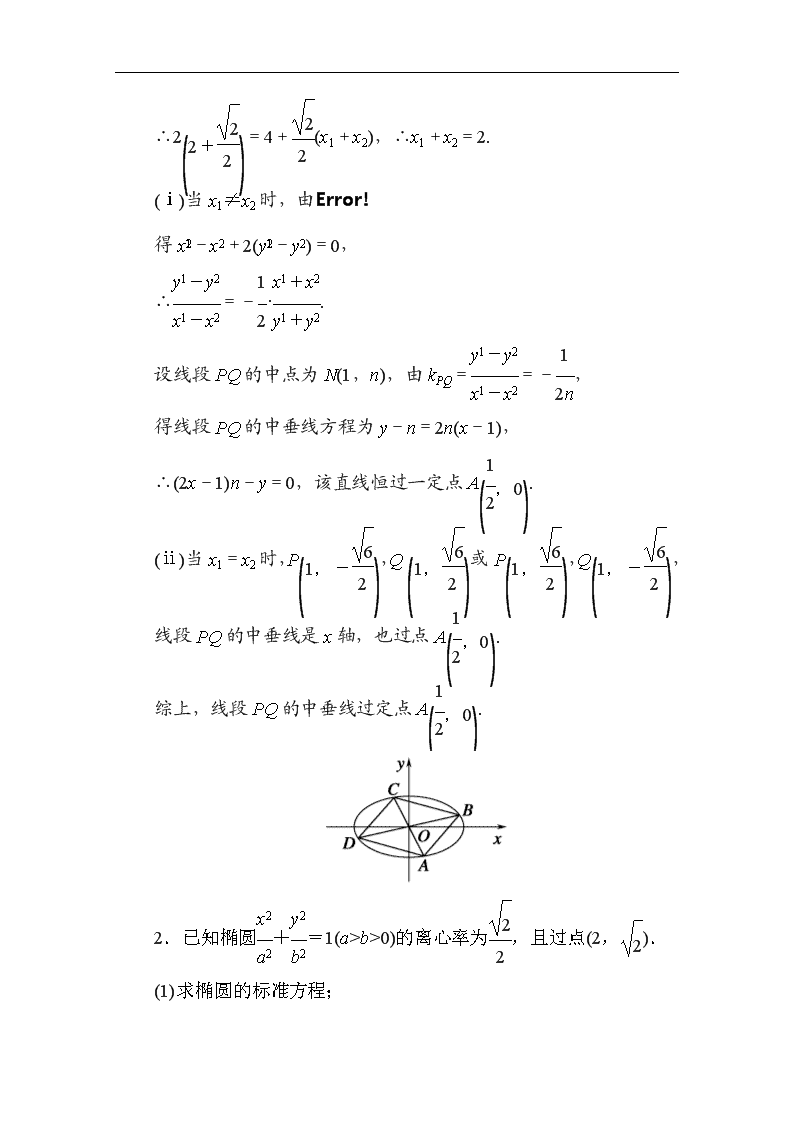人教版高三数学总复习课时作业62 7页

课时作业62　圆锥曲线中的最值、范围与定值、定点问题 ‎1．已知椭圆C过点M，点F(－，0)是椭圆的左焦点，点P，Q是椭圆C上的两个动点，且|PF|，|MF|，|QF|成等差数列．‎ ‎(1)求椭圆C的标准方程；‎ ‎(2)求证：线段PQ的垂直平分线经过一个定点A.‎ 解：(1)设椭圆C的方程为＋＝1(a>b>0)，由已知，得解得 ‎∴椭圆的标准方程为＋＝1.‎ ‎(2)证明：设P(x1，y1)，Q(x2，y2)，由椭圆的标准方程为＋＝1，可知|PF|＝＝ ‎＝2＋x1，同理|QF|＝2＋x2，‎ ‎|MF|＝＝2＋，‎ ‎∵2|MF|＝|PF|＋|QF|，‎ ‎∴2＝4＋(x1＋x2)，∴x1＋x2＝2.‎ ‎(ⅰ)当x1≠x2时，由 得x－x＋2(y－y)＝0，‎ ‎∴＝－·.‎ 设线段PQ的中点为N(1，n)，由kPQ＝＝－，‎ 得线段PQ的中垂线方程为y－n＝2n(x－1)，‎ ‎∴(2x－1)n－y＝0，该直线恒过一定点A.‎ ‎(ⅱ)当x1＝x2时，P，Q或P，Q，‎ 线段PQ的中垂线是x轴，也过点A.‎ 综上，线段PQ的中垂线过定点A.‎ ‎2．已知椭圆＋＝1(a>b>0)的离心率为，且过点(2，)．‎ ‎(1)求椭圆的标准方程；‎ ‎(2)四边形ABCD的顶点在椭圆上，且对角线AC，BD过原点O，若kAC·kBD＝－.‎ 求证：四边形ABCD的面积为定值．‎ 解：(1)由题意e＝＝，＋＝1，又a2＝b2＋c2，解得a2＝8，b2＝4，故椭圆的标准方程为＋＝1.‎ ‎(2)证明：设直线AB的方程为y＝kx＋m，A(x1，y1)，B(x2，y2)，联立得(1＋2k2)x2＋4kmx＋2m2－8＝0，‎ Δ＝(4km)2－4(1＋2k2)(2m2－8)＝8(8k2－m2＋4)>0，①‎ 由根与系数的关系得 ‎∵kAC·kBD＝－＝－，∴＝－，‎ ‎∴y1y2＝－x1x2＝－·＝－.‎ 又y1y2＝(kx1＋m)(kx2＋m)‎ ‎＝k2x1x2＋km(x1＋x2)＋m2‎ ‎＝k2＋km＋m2＝，‎ ‎∴－＝，∴－(m2－4)＝m2－8k2，‎ ‎∴4k2＋2＝m2.‎ 设原点到直线AB的距离为d，则 S△AOB＝|AB|·d＝·|x2－x1|· ‎＝ ‎＝＝ ‎＝2，‎ ‎∴S四边形ABCD＝4S△AOB＝8，‎ 即四边形ABCD的面积为定值．‎ ‎3．在平面直角坐标系xOy中，动点P到两点(－，0)，(，0)的距离之和等于4，设点P的轨迹为曲线C，直线l过点E ‎(－1，0)且与曲线C交于A，B两点．‎ ‎(1)求曲线C的轨迹方程；‎ ‎(2)△AOB的面积是否存在最大值，若存在，求出△AOB的面积的最大值；若不存在，说明理由．‎ 解：(1)由椭圆定义可知，点P的轨迹C是以(－，0)，(，0)为焦点，长半轴长为2的椭圆．‎ 故曲线C的轨迹方程为＋y2＝1.‎ ‎(2)△AOB的面积存在最大值．‎ 因为直线l过点E(－1,0)，所以可设直线l的方程为x＝my－1或y＝0(舍)．由 整理得(m2＋4)y2－2my－3＝0，Δ＝(2m)2＋12(m2＋4)>0.‎ 设点A(x1，y1)，B(x2，y2)，其中y1>y2.‎ 解得y1＝，y2＝.‎ 则|y2－y1|＝.‎ 因为S△AOB＝|OE|·|y1－y2|＝ ‎＝.‎ 设t＝，t≥，g(t)＝t＋，则g′(t)＝1－，故当t≥时，g′(t)>0恒成立，则g(t)在区间[，＋∞)上为增函数，所以g(t)≥g()＝.‎ 所以S△AOB≤，当且仅当m＝0时取等号．‎ 所以S△AOB的最大值为.‎ ‎1．(2014·新课标全国卷Ⅰ)已知点A(0，－2)，椭圆E：＋＝1(a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点．‎ ‎(1)求E的方程；‎ ‎(2)设过点A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．‎ 解：(1)设F(c,0)，由条件知，＝，得c＝.‎ 又＝，所以a＝2，b2＝a2－c2＝1.‎ 故E的方程为＋y2＝1.‎ ‎(2)当l⊥x轴时不合题意，故设l：y＝kx－2，P(x1，y1)，Q(x2，y2)．‎ 将y＝kx－2代入＋y2＝1得 ‎(1＋4k2)x2－16kx＋12＝0.‎ 当Δ＝16(4k2－3)>0，即k2>时，x1,2＝.‎ 从而|PQ|＝|x1－x2|＝.‎ 又点O到直线PQ的距离d＝.所以△OPQ的面积 S△OPQ＝d·|PQ|＝.‎ 设＝t，则t>0，S△OPQ＝＝.‎ 因为t＋≥4，当且仅当t＝2，即k＝±时等号成立，且满足Δ>0.‎ 所以，当△OPQ的面积最大时，l的方程为 y＝x－2或y＝－x－2.‎ ‎2．已知椭圆＋＝1(a>b>0)经过点M(，1)，离心率为.‎ ‎(1)求椭圆的标准方程．‎ ‎(2)已知点P(，0)，若A，B为已知椭圆上两动点，且满足·＝－2，试问直线AB是否恒过定点？若恒过定点，请给出证明，并求出该定点的坐标；若不过，请说明理由．‎ 解：(1)由题意得＝，①‎ 因为椭圆经过点M(，1)，所以＋＝1.②‎ 又a2＝b2＋c2，③‎ 由①②③，解得a2＝8，b2＝c2＝4.‎ 所以椭圆方程为＋＝1.‎ ‎(2)①当直线AB与x轴不垂直时，设直线的方程为y＝kx＋m，代入＋＝1，消去y整理得(2k2＋1)x2＋4kmx＋2m2－8＝0.‎ 由Δ>0，得8k2＋4－m2>0，(*)‎ 设A(x1，y1)，B(x2，y2)，则x1＋x2＝－，x1x2＝.‎ 所以·＝(x1－)(x2－)＋y1y2‎ ‎＝(x1－)(x2－)＋(kx1＋m)(kx2＋m)‎ ‎＝(k2＋1)x1x2＋(km－)(x1＋x2)＋6＋m2＝－2，‎ 得(k2＋1)x1x2＋(km－)(x1＋x2)＋8＋m2＝0，‎ ‎(k2＋1)·＋(km－)·＋8＋m2＝0，‎ 整理得(m＋2k)2＝0，从而m＝－k，且满足(*)，‎ 所以直线AB的方程为y＝k，故直线AB经过定点.‎ ‎②当直线AB与x轴垂直时，若直线为x＝，此时点A，B的坐标分别为，，亦有·＝－2.‎ 综上，直线AB经过定点.‎