高中数学必修2教案：2_1_1平面 (3) 6页

第一课时 平 面 ‎（一）教学目标 ‎1．知识与技能 ‎（1）利用生活中的实物对平面进行描述；‎ ‎（2）掌握平面的表示法及水平放置的直观图 ‎（3）掌握平面的基本性质及作用；‎ ‎（4）培养学生的空间想象能力.‎ ‎2．过程与方法 ‎（1）通过师生的共同讨论，使学生对平面有了感性认识；‎ ‎（2）让学生归纳整理本节所学知识.‎ ‎3．情感、态度与价值观 使用学生认识到我们所处的世界是一个三维空间，进而增强了学习的兴趣.‎ ‎（二）教学重点、难点 重点：1、平面的概念及表示；‎ ‎2、平面的基本性质，注意他们的条件、结论、作用、图形语言及符号语言.‎ 难点：平面基本性质的掌握与运用.‎ ‎（三）教学方法 师生共同讨论法 教学过程 教学内容 师生互动 设计意图 新课导入 日常生活中有哪些东西给我们以平面的形象？‎ 师：生活中常见的如黑板、平整的操场、桌面，平静的湖面等，都给我们以平面的印象，你们能举出更多的例子吗？引导学生观察、思考、举例和相交交流，教师对学生活动给予评价，点出主题.‎ 培养学生感性认识 探索新知 ‎1．平面的概念 随堂练习 判定下列命题是否正确：‎ ‎①书桌面是平面；‎ ‎②8个平面重叠起来要比6个平面重叠起来厚；‎ ‎③有一个平面的长是‎50m，宽是‎20m；‎ ‎④平面是绝对的平，无厚度，可以无限延展的抽象的数学概念.‎ 师：刚才大家所讲的一些物体都给我们以平面的印象，几何里所说的平面就是从这样的一些物体中抽象出来的，但是，几何里的平面是向四周无限伸展的，现在请大家判定下列命题是否正确？‎ 生：平面是没有厚度，无限延展的；所以①②③错误；④正确.‎ 加深学生对平面概念的理解.‎ 探索新知 ‎2．平面的画法及表示 ‎（1）平面的画法 通常我们把水平的平面画成平行四边形，用平行四边形表示平面，其中平行四边形的锐角通常画成45°‎ 师：在平面几何中，怎样画直线？(一学生上黑板画)‎ ‎，且横边长等于其邻边长的2倍.如果一个平面被另一个平面遮挡住. 我们常把被遮挡的部分用垂线画出来.‎ ‎（2）平面的表示 法1：平面，平面.‎ 法2：平面ABCD，平面AC或平面BD.‎ ‎（3）点与平面的关系 平面内有无数个点，平面可看成点的集合. 点A在平面内，记作：A. 点B在平面外，记作：B.‎ 师：这位同学画的实质上是直线的部分，通过想象两端无限延伸而认为是一条直线，仿照直线的画法，我们可以怎样画一个平面？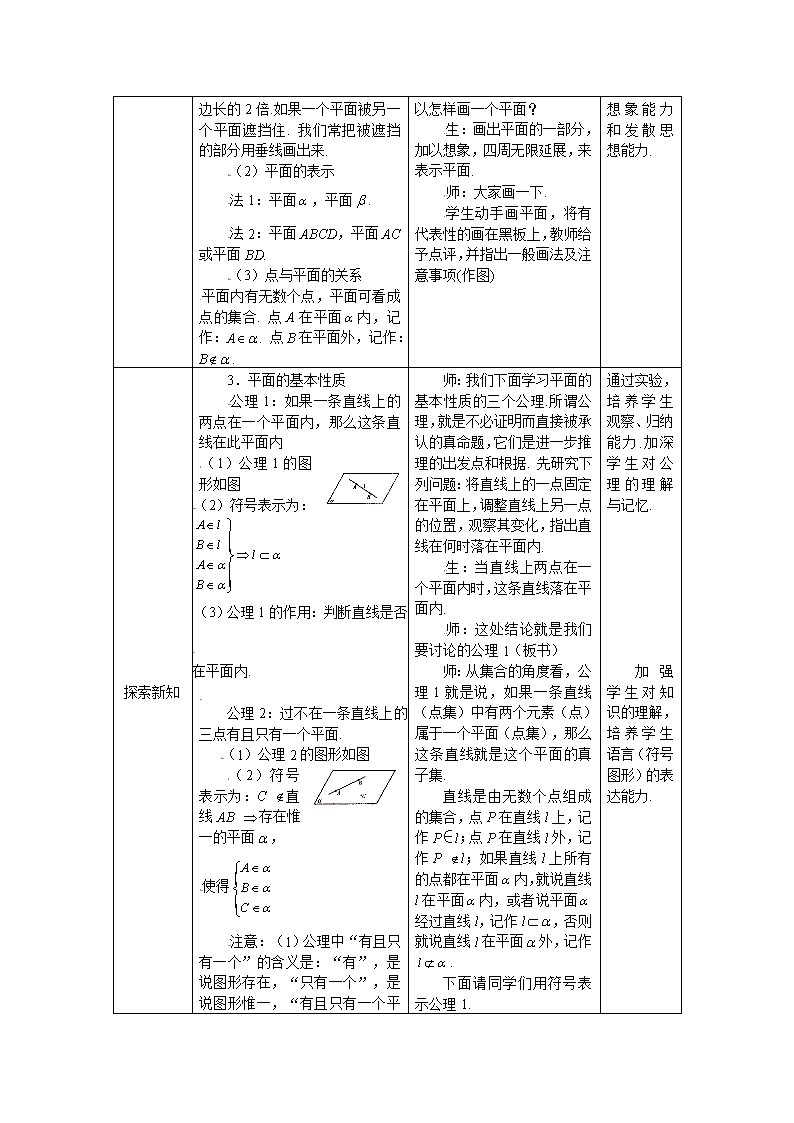‎ 生：画出平面的一部分，加以想象，四周无限延展，来表示平面.‎ 师：大家画一下.‎ 学生动手画平面，将有代表性的画在黑板上，教师给予点评，并指出一般画法及注意事项(作图)‎ 加深学生对平面概念的理解，培养学生知识迁移能力，空间想象能力和发散思想能力.‎ 探索新知 ‎3．平面的基本性质 公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内 ‎（1）公理1的图形如图 ‎（2）符号表示为：‎ ‎（3）公理1的作用：判断直线是否在平面内.‎ 公理2：过不在一条直线上的三点有且只有一个平面.‎ ‎（1）公理2的图形如图 ‎（2）符号表示为：C 直线AB 存在惟一的平面，‎ 使得 注意：（1）公理中“有且只有一个”的含义是：“有”，是说图形存在，“只有一个”，是说图形惟一，“‎ 师：我们下面学习平面的基本性质的三个公理.所谓公理，就是不必证明而直接被承认的真命题，它们是进一步推理的出发点和根据. 先研究下列问题：将直线上的一点固定在平面上，调整直线上另一点的位置，观察其变化，指出直线在何时落在平面内.‎ 生：当直线上两点在一个平面内时，这条直线落在平面内.‎ 师：这处结论就是我们要讨论的公理1（板书）‎ 师：从集合的角度看，公理1就是说，如果一条直线（点集）中有两个元素（点）属于一个平面（点集），那么这条直线就是这个平面的真子集.‎ 直线是由无数个点组成的集合，点P在直线l上，记作P∈l；点P在直线l外，记作P l；如果直线l上所有的点都在平面内，就说直线l在平面内，或者说平面经过直线l，记作l，否则就说直线l在平面外，记作.‎ 下面请同学们用符号表示公理1.‎ 通过实验，培养学生观察、归纳能力.加深学生对公理的理解与记忆.‎ 加强学生对知识的理解，培养学生语言（符号图形）的表达能力.‎ 有且只有一个平面”的意思是说“经过不在同一直线上的三个点的平面是有的，而且只有一个”，也即不共线的三点确定一个平面.‎ ‎“有且只有一个平面”也可以说成“确定一个平面.”‎ ‎（2）过A、B、C三点的平面可记作“平面ABC”‎ 公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.‎ ‎（1）公理3的图形如图 ‎（2）符号表示为：‎ ‎（3）公理3作用：判断两个平面是否相交.‎ 学生板书，教师点评并完善.‎ 大家回忆一下几点可以确定一条直线 生：两点可确定一条直线.‎ 师：那么几点可以确定上个平面呢？‎ 学生思考，讨论然后回答.‎ 生1：三点可确定一个平面 师：不需要附加条件吗？‎ 生2：还需要三点不共线 师：这个结论就是我们要讨论的公理2‎ 师投影公理2图示与符号表示，分析注意事项.‎ 师：下面请同学们观察教室的天花板与前面的墙壁，思考这两个平面的公共点有多少个？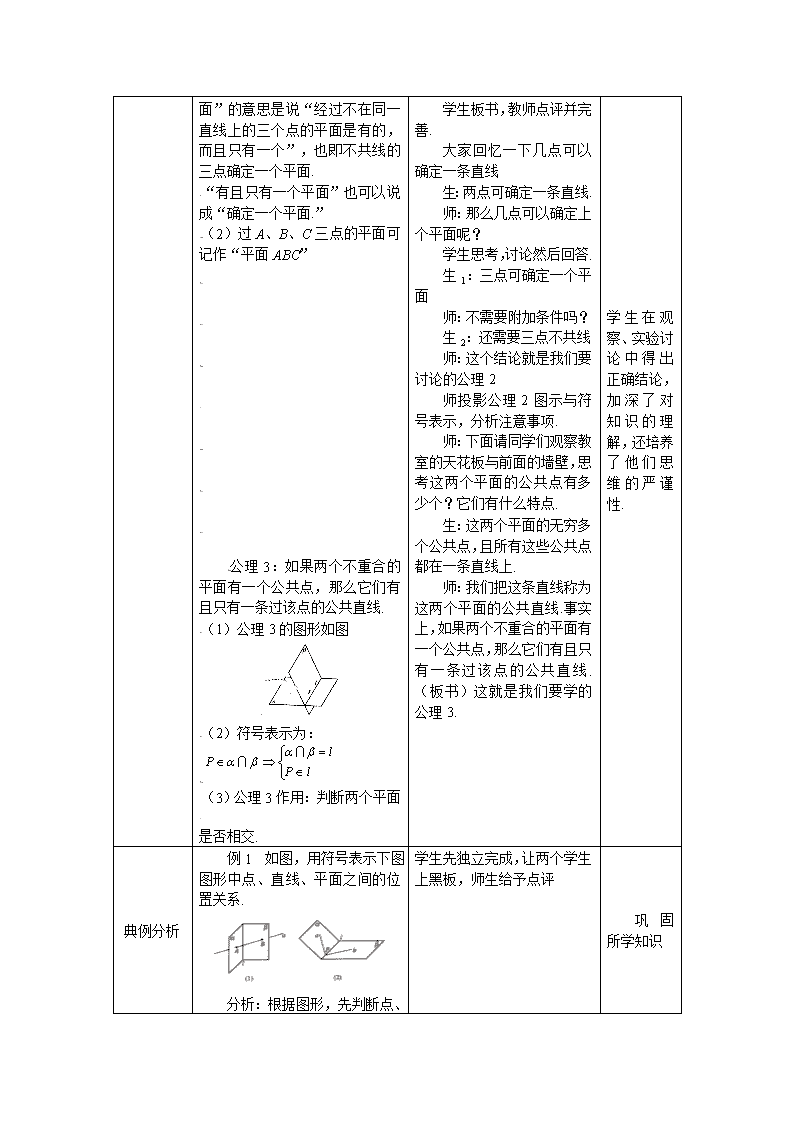它们有什么特点.‎ 生：这两个平面的无穷多个公共点，且所有这些公共点都在一条直线上.‎ 师：我们把这条直线称为这两个平面的公共直线.事实上，如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.（板书）这就是我们要学的公理3.‎ 学生在观察、实验讨论中得出正确结论，加深了对知识的理解，还培养了他们思维的严谨性.‎ 典例分析 例1 如图，用符号表示下图图形中点、直线、平面之间的位置关系.‎ 学生先独立完成，让两个学生上黑板，师生给予点评 巩固所学知识 分析：根据图形，先判断点、直线、平面之间的位置关系，然后用符号表示出来.‎ 解：在（1）中，，，.‎ 在（2）中，，，，，.‎ 随堂练习 ‎1．下列命题正确的是（ ）‎ A．经过三点确定一个平面 B．经过一条直线和一个点确定一个平面 C．四边形确定一个平面 D．两两相交且不共点的三条直线确定一个平面 ‎2．（1）不共面的四点可以确定几个平面？‎ ‎（2）共点的三条直线可以确定几个平面？‎ ‎3．判断下列命题是否正确，正确的在括号内画“√”，错误的画“×”.‎ ‎（1）平面与平面相交，它们只有有限个公共点. （ ）‎ ‎（2）经过一条直线和这条直线外的一点，有且只有一个平面.‎ ‎（ ）‎ ‎（3）经过两条相交直线，有且只有一个平面. （ ）‎ ‎（4）如果两个平面有三个不共线的公共点，那么这两个平面重合. （ ）‎ ‎4．用符号表示下列语句，并画出相应的图形：‎ ‎（1）点A在平面内，但点B在平面外；‎ ‎（2）直线a经过平面外的一点M；‎ ‎（3）直线a既在平面内，又在平面内.‎ 学生独立完成 答案：‎ ‎1．D ‎2．（1）不共面的四点可确定4个平面.‎ ‎（2）共点的三条直线可确定一个或3个平面.‎ ‎3．（1）×（2）√（3）√（4）√‎ ‎4．（1）A，B.‎ ‎（2）M，M.‎ ‎（3）a，a.‎ 巩固所学知识 归纳总结 ‎1．平面的概念，画法及表示方法.‎ ‎2．平面的性质及其作用 ‎3．符号表示 ‎4．注意事项 学生归纳、总结教学、补充完善.‎ 回顾、反思、归纳知识，提升自我整合知识的能力，培养思维严谨性固化知识，提升能力.‎ 课后作业 ‎2.1第一课时 习案 学生独立完成 备选例题 例1 已知：a，b，c，d是不共点且两两相交的四条直线，求证：a，b，c，d共面．‎ 证明 1o若当四条直线中有三条相交于一点，不妨设a，b，c相交于一点A，‎ 但AÏd，如图1．∴直线d和A确定一个平面α．‎ 又设直线d与a，b，c分别相交于E，F，G，‎ α b a d c G F E A a b c d α H K 图1‎ 图2‎ 则A，E，F，G∈α．‎ ‎∵A，E∈α，A，E∈a，∴aα．‎ 同理可证bα，cα．‎ ‎∴a，b，c，d在同一平面α内．‎ ‎2o当四条直线中任何三条都不共点时，如图2．‎ ‎∵这四条直线两两相交，则设相交直线a，b确定一个平面α．‎ 设直线c与a，b分别交于点H，K，则H，K∈α．‎ 又 H，K∈c，∴c,则cα．‎ 同理可证dα．‎ ‎∴a，b，c，d四条直线在同一平面α内．‎ 说明：证明若干条线(或若干个点)共面的一般步骤是：首先根据公理3或推论，由题给条件中的部分线(或点)确定一个平面，然后再根据公理1证明其余的线(或点)均在这个平面内．本题最容易忽视“三线共点”这一种情况．因此，在分析题意时，应仔细推敲问题中每一句话的含义．‎ 例2 正方体ABCD—A1B‎1C1D1中，对角线A‎1C与平面BDC1交于点O，AC、BD交于点M，求证：点C1、O、M共线.‎ M O B1‎ C1‎ D1‎ A1‎ D C B A 分析：要证若干点共线的问题，只需证这些点同在两个相交平面内即可.‎ 解答：如图所示A‎1A∥C‎1C确定平面A‎1C O∈平面A1C ‎ A‎1C平面A‎1C ‎ 又O∈A‎1C 平面BC1D∩直线A‎1C = O ‎ O∈平面BC1D O在平面A‎1C与平面BC1D的交线上.‎ AC∩BD = MM∈平面BC1D 且M∈平面A‎1C ‎ 平面BC1D∩平面A‎1C = C‎1M ‎ O∈C‎1M，即O、C1、M三点共线.‎ 评析：证明点共线的问题，一般转化为证明这些点同是某两个平面的公共点.这样，可根据公理2证明这些点都在这两个平面的公共直线上.‎