人教版高三数学总复习课时作业51 10页

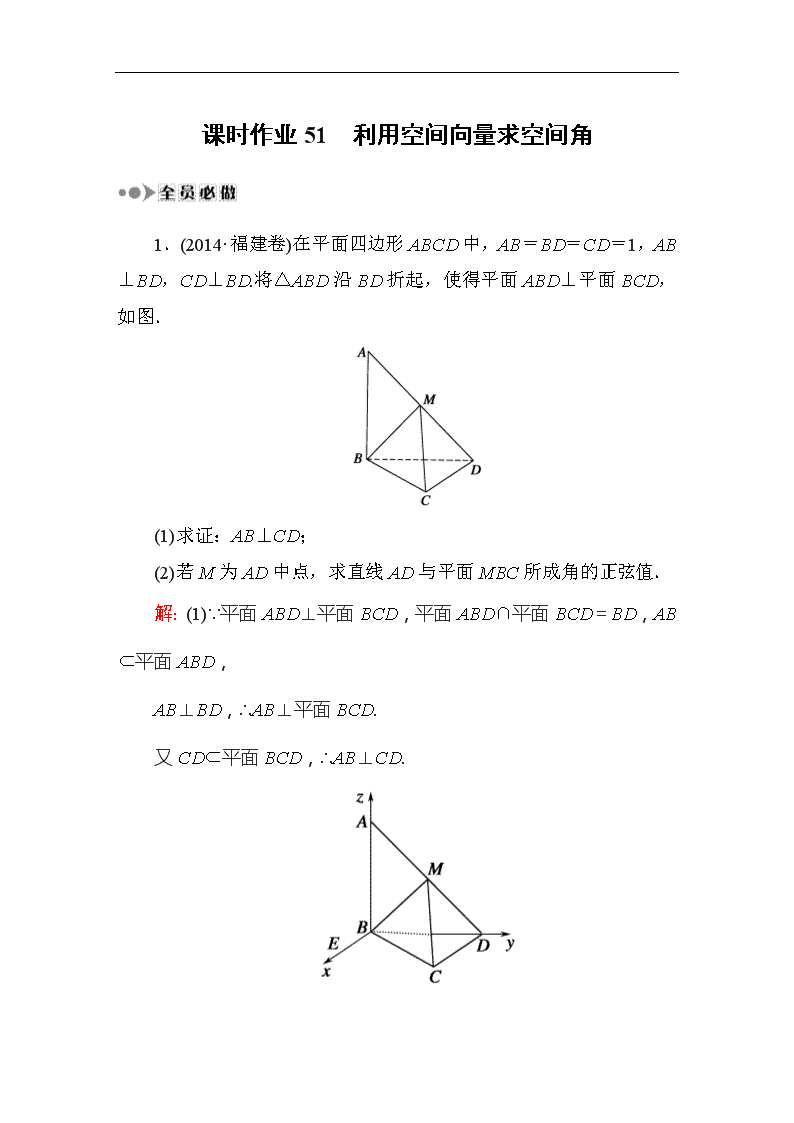
课时作业51　利用空间向量求空间角 ‎1．(2014·福建卷)在平面四边形ABCD中，AB＝BD＝CD＝1，AB⊥BD，CD⊥BD.将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．‎ ‎(1)求证：AB⊥CD；‎ ‎(2)若M为AD中点，求直线AD与平面MBC所成角的正弦值．‎ 解：(1)∵平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，AB⊂平面ABD，‎ AB⊥BD，∴AB⊥平面BCD.‎ 又CD⊂平面BCD，∴AB⊥CD.‎ ‎(2)过点B在平面BCD内作BE⊥BD，如图．‎ 由(1)知AB⊥平面BCD，BE⊂平面BCD，BD⊂平面BCD，‎ ‎∴AB⊥BE，AB⊥BD.‎ 以B为坐标原点，分别以，，的方向为x轴，y轴，z轴的正方向建立空间直角坐标系．‎ 依题意，得B(0,0,0)，C(1,1,0)，D(0,1,0)，‎ A(0,0,1)，M(0，，)，‎ 则＝(1,1,0)，＝(0，，)，＝(0,1，－1)．‎ 设平面MBC的法向量n＝(x0，y0，z0)，‎ 则即 取z0＝1，得平面MBC的一个法向量n＝(1，－1,1)．‎ 设直线AD与平面MBC所成角为θ，‎ 则sinθ＝|cosn，|＝＝，‎ 即直线AD与平面MBC所成角的正弦值为.‎ ‎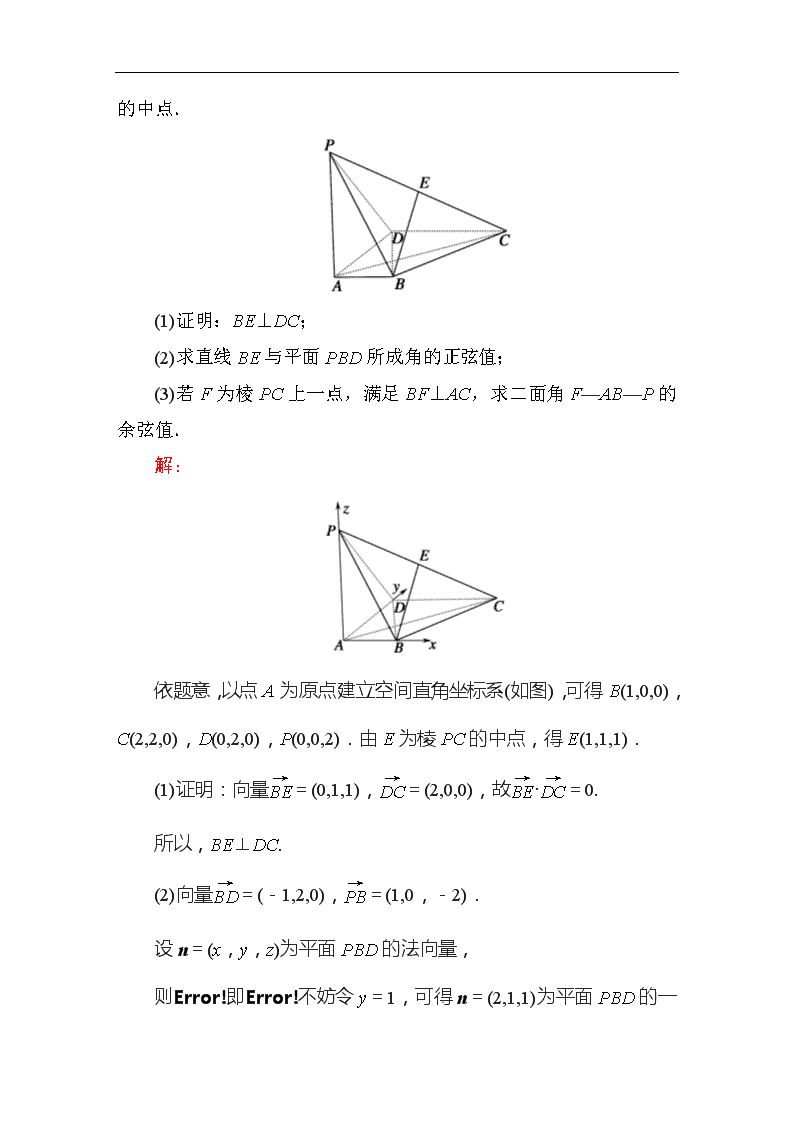2．(2014·天津卷)如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．‎ ‎(1)证明：BE⊥DC；‎ ‎(2)求直线BE与平面PBD所成角的正弦值；‎ ‎(3)若F为棱PC上一点，满足BF⊥AC，求二面角F—AB—P的余弦值．‎ 解：‎ 依题意，以点A为原点建立空间直角坐标系(如图)，可得B(1,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2)．由E为棱PC的中点，得E(1,1,1)．‎ ‎(1)证明：向量＝(0,1,1)，＝(2,0,0)，故·＝0.‎ 所以，BE⊥DC.‎ ‎(2)向量＝(－1,2,0)，＝(1,0，－2)．‎ 设n＝(x，y，z)为平面PBD的法向量，‎ 则即不妨令y＝1，可得n＝(2,1,1)为平面PBD的一个法向量．于是有 cosn，＝＝＝.‎ 所以，直线BE与平面PBD所成角的正弦值为.‎ ‎(3)向量＝(1,2,0)，＝(－2，－2,2)，＝(2,2,0)， ‎＝(1,0,0)．‎ 由点F在棱PC上，设＝λ，0≤λ≤1.‎ 故＝＋＝＋λ＝(1－2λ，2－2λ，2λ)．‎ 由BF⊥AC，得·＝0，‎ 因此，2(1－2λ)＋2(2－2λ)＝0，解得λ＝.‎ 即＝.‎ 设n1＝(x，y，z)为平面FAB的法向量，则 即不妨令z＝1，‎ 可得n1＝(0，－3,1)为平面FAB的一个法向量．‎ 取平面ABP的法向量n2＝(0,1,0)，则 cosn1，n2＝＝＝－.‎ 易知，二面角F—AB—P是锐角，所以其余弦值为.‎ ‎3．在长方体ABCD—A1B‎1C1D1中，AB＝，AD＝1，M是线段AD的中点．‎ ‎(1)试在平面ABCD内过M点作出与平面A1B1CD平行的直线l，说明理由，并证明：l⊥平面AA1D1D；‎ ‎(2)若(1)中的直线l交直线AC于点N，且二面角A—A1N—M 的余弦值为，求AA1的长．‎ 解：(1)在平面ABCD内过M点作直线l∥DC，‎ ‎∵l⊄平面A1B1CD，DC⊂平面A1B1CD，‎ ‎∴l∥平面A1B1CD.‎ 在长方体ABCD—A1B‎1C1D1中，DC⊥AD，DC⊥DD1，‎ 则l⊥AD，l⊥DD1.‎ 又AD∩DD1＝D，∴l⊥平面AA1D1D.‎ ‎(2)由(1)知，l∥DC且M是线段AD的中点，‎ ‎∴N是线段AC的中点．‎ 设AA1＝h，以A1为坐标原点，分别以A1B1，A1D1，A‎1A所在直线为x轴，y轴，z轴，建立空间直角坐标系A1—xyz.则A1(0,0,0)，A(0,0，h)，N(，，h)，M(0，，h)．‎ ‎∴＝(0,0，h)，＝(，，h)，＝(0，，h)，＝(，0,0)．‎ 设平面A1AN的法向量n1＝(x1，y1，z1)，‎ 则，∴，‎ 取x1＝1，∴n1＝(1，－，0)．‎ 设平面A1MN的法向量n2＝(x2，y2，z2)，‎ 则，∴，‎ 取z2＝1，∴n2＝(0，－2h,1)．‎ ‎∵二面角A—A1N—M的余弦值为，‎ ‎∴cos〈n1，n2〉＝，即＝，‎ ‎∴＝，‎ 解得h＝1，即AA1＝1.‎ ‎1．等边三角形ABC的边长为3，点D、E分别是边AB、AC上的点，且满足＝＝(如图1)．将△ADE沿DE折起到△A1DE的位置，使二面角A1—DE—B为直二面角，连接A1B、A‎1C(如图2)．‎ ‎(1)求证：A1D⊥平面BCED；‎ ‎(2)在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB的长，若不存在，请说明理由．‎ 解：(1)证明：因为等边△ABC的边长为3，且＝＝，所以AD＝1，AE＝2.在△ADE中，∠DAE＝60°，‎ 由余弦定理得DE＝＝.因为AD2＋DE2＝AE2，所以AD⊥DE.‎ 折叠后有A1D⊥DE，因为二面角A1—DE—B是直二面角，‎ 所以平面A1DE⊥平面BCED，又平面A1DE∩平面BCED＝DE，A1D⊂平面A1DE，A1D⊥DE，所以A1D⊥平面BCED.‎ ‎(2)由(1)的证明，可知ED⊥DB，A1D⊥平面BCED，以D为坐标原点，以射线DB、DE、DA1分别为x轴、y轴、z轴的正半轴，建立空间直角坐标系D—xyz如右图，设PB＝‎2a(0≤‎2a≤3)，过P作PH∥DE，则BH＝a，PH＝a，DH＝2－a，所以A1(0,0,1)，P(2－a，a,0)，E(0，，0)，所以＝(a－2，－a,1)，因为ED⊥平面A1BD，所以平面A1BD的一个法向量为＝(0，，0)，‎ 因为直线PA1与平面A1BD所成的角为60°，‎ 所以sin60°＝＝＝，‎ 解得a＝，即PB＝‎2a＝，满足0≤‎2a≤3，符合题意，所以在线段BC上存在点P，使直线PA1与平面A1BD所成的角为60°，此时PB＝.‎ ‎2．如下图，△ABC中，AB＝2，BC＝1，∠ABC＝90°，D，E分别为AB，AC上的点，DE∥BC，将△ADE沿DE折到△A′DE的位置，使平面A′DE⊥平面BCED.‎ ‎(1)当D为AB的中点时，设平面A′BC与平面A′DE所成的二面角的平面角为α(0<α<)，直线A′C与平面A′DE所成角为β，求tan(α＋β)的值；‎ ‎(2)当D点在AB边上运动时，求四棱锥A′—BCED体积的最大值．‎ 解：‎ ‎(1)DB，DE，DA′两两垂直，故以点D为原点．‎ DB，DE，DA′所在直线分别为x，y，z轴，建立直角坐标系(如图)，则D(0,0,0)，B(1,0,0)，C(1,1,0)，E(0，，0)，A′(0,0,1)‎ ＝(1,0，－1)，＝(0,1,0)，设平面A′BC的一个法向量为n＝(x，y，z)‎ 由得，故可取n＝(1,0,1)，又平面A′DE的一个法向量为＝(1,0,0)‎ cosα＝|cos〈n，〉|＝|＝＝，‎ ‎∴tanα＝1‎ 由于平面A′DE的一个法向量为 ＝(1,0,0)，CA′＝(－1，－1,1)‎ 所以sinβ＝|cos〈CA′，〉|＝|＝＝ cosβ＝，∴tanβ＝ ‎∴tan(α＋β)＝＝3＋2 ‎(2)设A′D＝x，x∈(0,2)，则DE＝，BD＝2－x，‎ 设VA′—BCED＝··x＝＝v(x)，x∈(0,2)，‎ v′(x)＝，令v′(x)＝0，x＝.‎ v(x)在(0，)递增，在(，2)递减，‎ ‎∴[v(x)]max＝v()＝.‎ 即所求最大体积为.‎