高中数学第7章（第18课时）圆的方程1 6页

课 题：7.6圆的方程（一）‎ 教学目的：‎ 使学生掌握圆的标准方程的特点，能根据所给有关圆心、半径的具体条件准确地写出圆的标准方程，能运用圆的标准方程正确地求出其圆心和半径，解决一些简单的实际问题，并会推导圆的标准方程． ‎ 教学重点：圆的标准方程的推导步骤；根据具体条件正确写出圆的标准方程 ‎ 教学难点：运用圆的标准方程解决一些简单的实际问题 ‎ 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 内容分析：‎ ‎ 学习了“曲线与方程“之后，作为一般曲线典体例子，安排了本节的“圆的方程” 圆是学生比较熟悉的曲线，在初中曾经学习过圆的有关知识，本节内容是在初中所学知识及前几节内容的基础上，进一步运用解析法研究它的方程，它与其他图形的位置关系及其应用 同时，由于圆也是特殊的圆锥曲线，因此，学习了圆的方程，就为后面学习其它圆锥曲线的方程奠定了基础 也就是说，本节内容在教材体系中起到承上启下的作用，具有重要的地位，在许多实际问题中也有着广泛的应用 由于“圆的方程”一节内容的基础性和应用的广泛性，对圆的标准方程、一般方程的要求层次是“掌握”；因为是第一次系统地介绍参数方程，对参数方程的学习有一个循序渐进的过程，因而对圆的参数方程只要求“理解”，今后讲圆锥曲线时还有所涉及 结合本节的内容的特点，可以向学生渗透多种数学思想方法，同时对学生的观察类比、创新等多种能力的培养也十分有利 在运用多种方法求圆的方程中，可培养学生大胆探索创新的精神；通过知识的实际运用和采用多媒体手段，培养学生学习数学的兴趣；而一些曲线上动点的变化，和方程形式，解法的多样，也有助于学生树立辩证唯物主义的运动观和普遍联系的观点 ‎ 遵循从特殊到一般的原则，只有把圆的标准方程学透了，再过渡到学圆的一般也就不难，它们可以通过形式上的互相转化而解决 因而本节的重点是圆的标准方程及直线与圆的位置关系（尤其是圆的切线） 又由于圆的一般方程中含有三个参变数D、E、F，对它的理解带来一定的困难，因而本节的难点是对圆的一般方程的认识、掌握和运用 突破难点的关键是抓住一般方程的特点，把握住求圆的方程的两个基本要素：圆心坐标和半径 依照大纲，本节分为三个课时进行教学 第一课时讲解圆的标准方程 ‎ 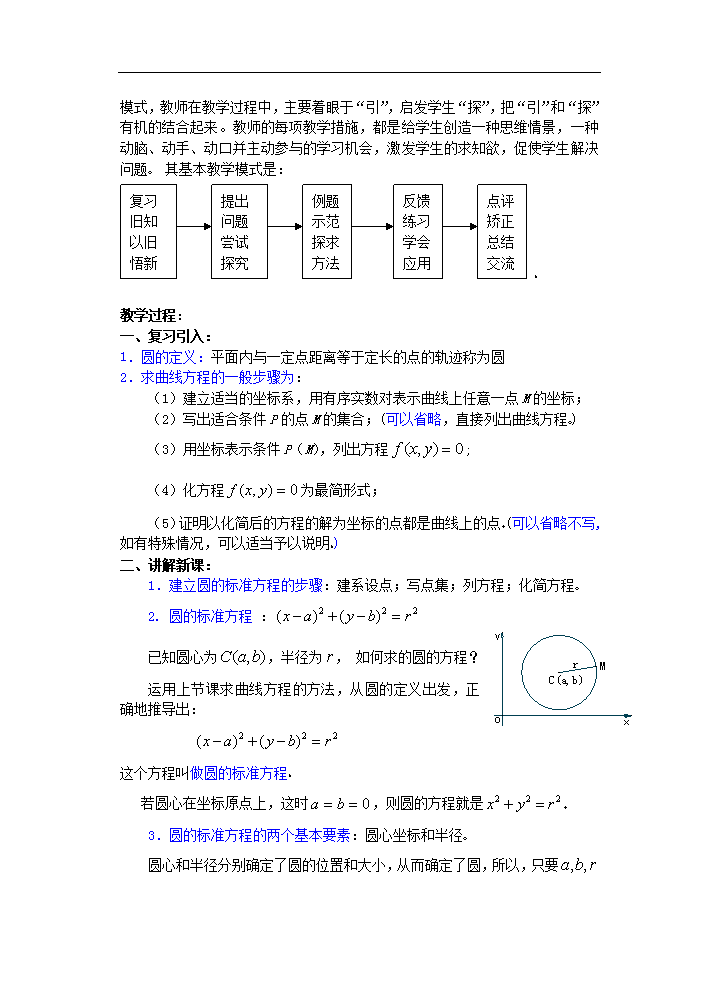为了激发学生的主体意识，教学生学会学习和学会创造，同时培养学生的应用意识，本节内容可采用“引导探究”型教学模式进行教学设计 所谓“引导探究”‎ 是教师把教学内容设计为若干问题，从而引导学生进行探究的课堂教学模式，教师在教学过程中，主要着眼于“引”，启发学生“探”，把“引”和“探”有机的结合起来。教师的每项教学措施，都是给学生创造一种思维情景，一种动脑、动手、动口并主动参与的学习机会，激发学生的求知欲，促使学生解决问题 其基本教学模式是：‎ 复习 旧知 以旧 悟新 提出 问题 尝试 探究 例题 示范 探求 方法 反馈 练习 学会 应用 点评 矫正 总结 交流 ‎ ‎ 教学过程：‎ 一、复习引入： ‎ ‎1．圆的定义：平面内与一定点距离等于定长的点的轨迹称为圆 ‎2．求曲线方程的一般步骤为：‎ ‎（1）建立适当的坐标系，用有序实数对表示曲线上任意一点M的坐标；‎ ‎（2）写出适合条件P的点M的集合；(可以省略，直接列出曲线方程)‎ ‎（3）用坐标表示条件P（M），列出方程;‎ ‎（4）化方程为最简形式；‎ ‎（5）证明以化简后的方程的解为坐标的点都是曲线上的点(可以省略不写,如有特殊情况，可以适当予以说明)‎ 二、讲解新课：‎ ‎1．建立圆的标准方程的步骤：建系设点；写点集；列方程；化简方程 ‎ ‎2. 圆的标准方程 ：‎ 已知圆心为，半径为， 如何求的圆的方程？ ‎ 运用上节课求曲线方程的方法，从圆的定义出发，正确地推导出：‎ 这个方程叫做圆的标准方程 若圆心在坐标原点上，这时，则圆的方程就是 ‎3．圆的标准方程的两个基本要素：圆心坐标和半径 圆心和半径分别确定了圆的位置和大小，从而确定了圆，所以，只要 三个量确定了且＞0，圆的方程就给定了 这就是说要确定圆的方程，必须具备三个独立的条件 确定，可以根据条件，利用待定系数法来解决 三、讲解范例：‎ 例1 求以C(1,3)为圆心，并且和直线相切的圆的方程 解：已知圆心坐标C(1,3)，故只要求出圆的半径，就能写出圆的标准方程 因为圆C和直线相切，所以半径就等于圆心C到这条直线的距离 根据点到直线的距离公式，得 因此，所求的圆的方程是 ‎ ‎ 点评： 由本题可知，圆的标准方程是由圆心坐标和半径两因素决定的 而且圆的半径与圆的切线有着非常密切的联系，解题要注意运用圆的切线的性质 解题时画出草图可帮助思考 例2 已知圆的方程，求经过圆上一点的切线方程 ‎ 解：如图，设切线的斜率为，半径OM的斜率为 因为圆的切线垂直于过切点的半径，于是 ‎∵ ∴‎ 经过点M的切线方程是 ，‎ 整理得 ‎ 因为点在圆上，所以，所求切线方程是 点评： 用斜率的知识来求切线方程，这就是“代数方程”：即设出圆的切线方程，将其代入到圆的方程，得到一个关于或的一元二次方程，利用判别式进行求解，但此法不如用几何方法简练实用，几何方法就是利用圆心到直线的距离等于半径(本题利用了圆心到切点的距离为半径的知识)，由此确定了斜率的，从而得到点斜式的切线方程，以上两种方法只能求出存在斜率的切线，若斜率不存在，则要结合图形配补 ‎ 四、课堂练习：‎ ‎1．求下列各圆的标准方程：‎ ‎（1）圆心在上且过两点（2，0），（0，-4）；‎ ‎（2）圆心在直线上，且与直线切于点（2，-1）.‎ ‎（3）圆心在直线上，且与坐标轴相切 分析：从圆的标准方程可知，要确定圆的标准方程，可用待定系数法确定三个参数 解：（1）设圆心坐标为()，则所求圆的方程为,‎ ‎∵圆心在上，∴ ①‎ 又∵圆过（2，0），（0，-4）∴ ②‎ ‎ ③‎ 由①②③联立方程组，可得 ‎∴所求圆的方程为 ‎（2）∵圆与直线相切，并切于点M（2，-1），则圆心必在过点M（2，-1）且垂直于的直线：上， ‎ ‎，即圆心为C（1，-2），=,‎ ‎∴所求圆的方程为：‎ ‎（3）设所求圆的方程为,‎ ‎∵圆与坐标轴相切， ∴‎ 又∵圆心()在直线上，∴‎ 由，得 ‎∴所求圆的方程为：或 ‎2.已知圆求：‎ ‎（1）过点A（4，-3）的切线方程.（2）过点B（-5，2）的切线方程 分析：求过一点的切线方程，当斜率存在时可设为点斜式，利用圆心到切线的距离等于圆的半径列出方程，求出斜率k的值，斜率不存在时，结合图形验证；当然若过圆上一点的切线方程，可利用公式求得 解：（1）∵点A（4，-3）在圆上 ‎∴过点A的切线方程为：‎ ‎（2）∵点点B（-5，2）不在圆上，当过点B（-5，2）的切线的斜率存在时，设所求切线方程为，即 由，得∴此时切线方程为：‎ 当过点B（-5，2）的切线斜率不存在时，结合图形可知=-5，也是切线方程 综上所述，所求切线方程为：或=-5‎ 五、小结 ：圆的标准方程的概念及推导；如何求圆的标准方程；待定系数法 ‎ 六、课后作业：‎ 七、板书设计（略）‎ 八、课后记：‎