2019年高考试题——数学理（北京卷）原卷版 6页

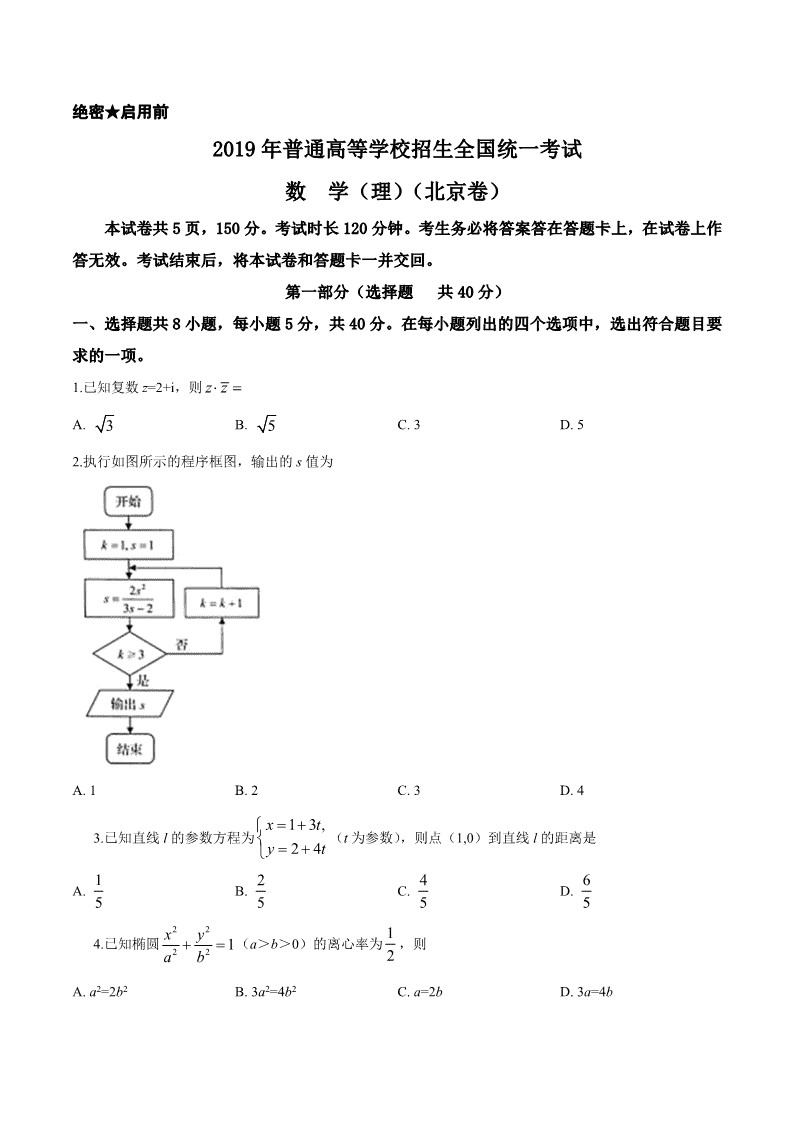
绝密★启用前 2019 年普通高等学校招生全国统一考试 数 学（理）（北京卷） 本试卷共 5 页，150 分。考试时长 120 分钟。考生务必将答案答在答题卡上，在试卷上作 答无效。考试结束后，将本试卷和答题卡一并交回。 第一部分（选择题 共 40 分） 一、选择题共 8 小题，每小题 5 分，共 40 分。在每小题列出的四个选项中，选出符合题目要 求的一项。 1.已知复数 z=2+i，则 A. B. C. 3 D. 5 2.执行如图所示的程序框图，输出的 s 值为 A. 1 B. 2 C. 3 D. 4 3.已知直线 l 的参数方程为 （t 为参数），则点（1,0）到直线 l 的距离是 A. B. C. D. 4.已知椭圆 （a＞b＞0）的离心率为 ，则 A. a2=2b2 B. 3a2=4b2 C. a=2b D. 3a=4b z z  3 5 1 3 , 2 4 x t y t      1 5 2 5 4 5 6 5 2 2 2 2 1x y a b  1 2 5.若 x，y 满足 ，且 y≥−1，则 3x+y 的最大值为 A. −7 B. 1 C. 5 D. 7 6.在天文学中，天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足 ，其 中星等为 m1 的星的亮度为 E2（k=1,2）.已知太阳的星等是–26.7，天狼星的星等是–1.45，则太阳与天狼星 的亮度的比值为 A. 1010.1 B. 10.1 C. lg10.1 D. 10–10.1 7.设点 A，B，C 不共线，则“ 与 的夹角为锐角”是“ ”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 8.数学中有许多形状优美、寓意美好的曲线，曲线 C： 就是其中之一（如图）.给出下列 三个结论： ①曲线 C 恰好经过 6 个整点（即横、纵坐标均为整数 点）； ②曲线 C 上任意一点到原点的距离都不超过 ； ③曲线 C 所围成的“心形”区域的面积小于 3. 其中，所有正确结论的序号是 A ① B. ② C. ①② D. ①②③ 第二部分（非选择题 共 110 分） 二、填空题共 6 小题，每小题 5 分，共 30 分。 9.函数 f(x)=sin22x 的最小正周期是__________． 10.设等差数列{an}的前 n 项和为 Sn，若 a2=−3，S5=−10，则 a5=__________，Sn 的最小值为__________． 11.某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为 1， | 1|x y  2 1 2 15 2– lg Em m E AB AC | | | |AB AC BC    2 2 1 | |x y x y   的 2 . 那么该几何体的体积为__________． 12.已知 l，m 是平面 外 两条不同直线．给出下列三个论断： ①l⊥m；②m∥ ；③l⊥ ． 以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________． 13.设函数 f（x）=ex+ae−x（a 为常数）．若 f（x）为奇函数，则 a=________；若 f（x）是 R 上的增函数，则 a 的取值范围是___________． 14.李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为 60 元/ 盒、65 元/盒、80 元/盒、90 元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到 120 元，顾客就少付 x 元．每笔订单顾客网上支付成功后，李明会得到支付款的 80%． ①当 x=10 时，顾客一次购买草莓和西瓜各 1 盒，需要支付__________元； ②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则 x 的最大值为__________． 三、解答题共 6 小题，共 80 分。解答应写出文字说明，演算步骤或证明过程。 15.在△ABC 中，a=3，b−c=2，cosB= ． （Ⅰ）求 b，c 的值； （Ⅱ）求 sin（B–C）的值． 16.如图，在四棱锥 P–ABCD 中，PA⊥平面 ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E 为 PD 的中点，点 F 在 PC 上，且 ． （Ⅰ）求证：CD⊥平面 PAD； （Ⅱ）求二面角 F–AE–P 的余弦值；  的   1 2 1 3 PF PC  （Ⅲ）设点 G 在 PB 上，且 ．判断直线 AG 是否在平面 AEF 内，说明理由． 17.改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解 某校学生上个月 A，B 两种移动支付方式的使用情况，从全校学生中随机抽取了 100 人，发现样本中 A，B 两种支付方式都不使用的有 5 人，样本中仅使用 A 和仅使用 B 的学生的支付金额分布情况如下： 交 付金额（元） 支付方式 （0,1000] （1000,2000] 大于 2000 仅使用 A 18 人 9 人 3 人 仅使用 B 10 人 14 人 1 人 （Ⅰ）从全校学生中随机抽取 1 人，估计该学生上个月 A，B 两种支付方式都使用的概率； （Ⅱ）从样本仅使用 A 和仅使用 B 学生中各随机抽取 1 人，以 X 表示这 2 人中上个月支付金额大于 1000 元的人数，求 X 的分布列和数学期望； （Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用 A 的学生中，随机抽查 3 人，发 现他们本月的支付金额都大于 2000 元．根据抽查结果，能否认为样本仅使用 A 的学生中本月支付金额大于 2000 元的人数有变化？说明理由． 18.已知抛物线 C：x2=−2py 经过点（2，−1）． （Ⅰ）求抛物线 C 的方程及其准线方程； （Ⅱ）设 O 为原点，过抛物线 C 的焦点作斜率不为 0 的直线 l 交抛物线 C 于两点 M，N，直线 y=−1 分别交 直线 OM，ON 于点 A 和点 B.求证：以 AB 为直径的圆经过 y 轴上的两个定点． 19.已知函数 . 2 3 PG PB  的 3 21( ) 4f x x x x   （Ⅰ）求曲线 斜率为 1 的切线方程； （Ⅱ）当 时，求证： ； （Ⅲ）设 ，记 在区间 上的最大值为 M（a），当 M（a）最小时， 求 a 的值． 20.已知数列{an}，从中选取第 i1 项、第 i2 项、…、第 im 项(i1