- 292.50 KB
- 2021-10-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
检测内容:5.1-5.2
得分________卷后分________评价________
一、选择题(每小题 5 分,共 40 分)
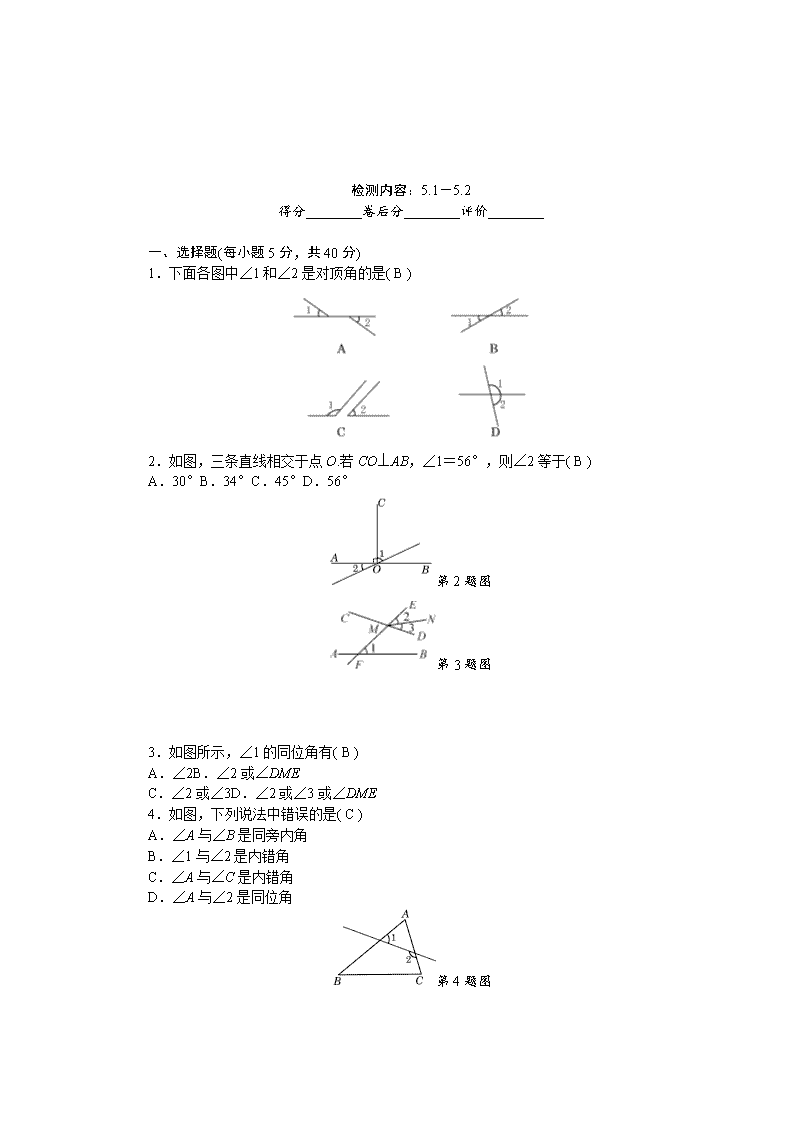
1.下面各图中∠1 和∠2 是对顶角的是( B )
2.如图,三条直线相交于点 O.若 CO⊥AB,∠1=56°,则∠2 等于( B )
A.30°B.34°C.45°D.56°
第 2 题图
第 3 题图
3.如图所示,∠1 的同位角有( B )
A.∠2B.∠2 或∠DME
C.∠2 或∠3D.∠2 或∠3 或∠DME
4.如图,下列说法中错误的是( C )
A.∠A 与∠B 是同旁内角
B.∠1 与∠2 是内错角
C.∠A 与∠C 是内错角
D.∠A 与∠2 是同位角
第 4 题图
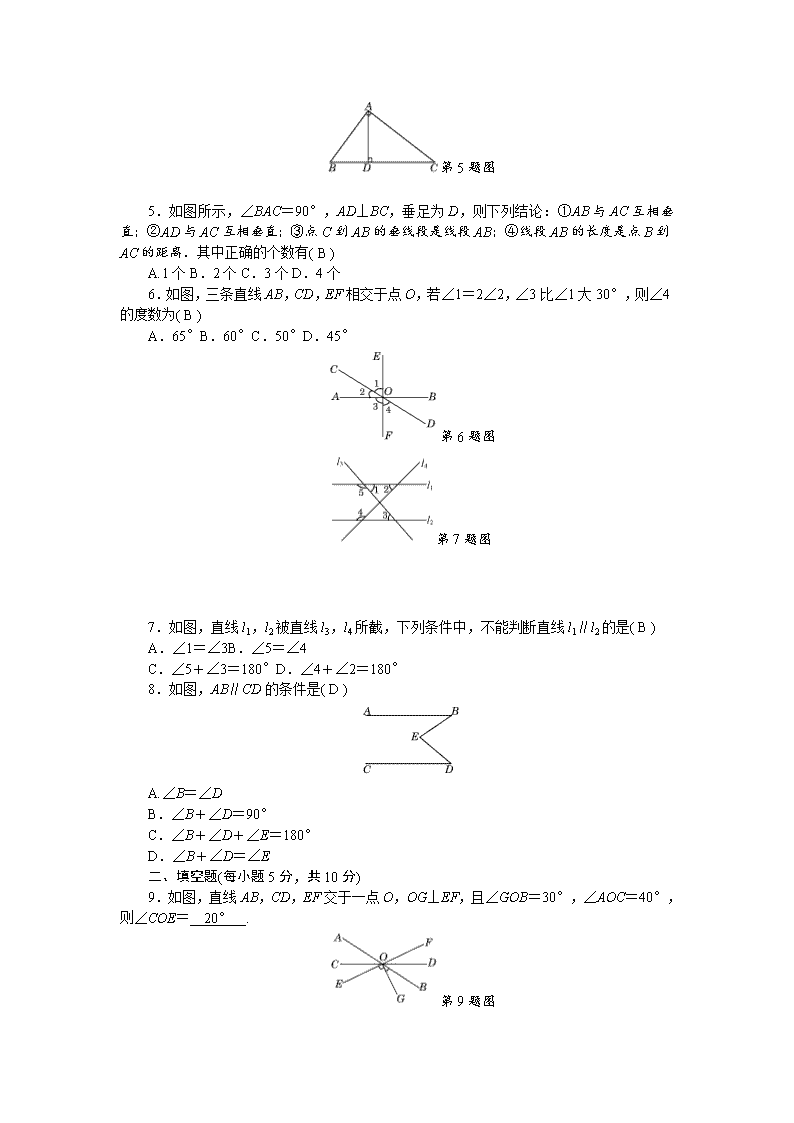
第 5 题图
5.如图所示,∠BAC=90°,AD⊥BC,垂足为 D,则下列结论:①AB 与 AC 互相垂
直;②AD 与 AC 互相垂直;③点 C 到 AB 的垂线段是线段 AB;④线段 AB 的长度是点 B 到
AC 的距离.其中正确的个数有( B )
A.1 个 B.2 个 C.3 个 D.4 个
6.如图,三条直线 AB,CD,EF 相交于点 O,若∠1=2∠2,∠3 比∠1 大 30°,则
∠4 的度数为( B )
A.65°B.60°C.50°D.45°
第 6 题图
第 7 题图
7.如图,直线 l1,l2 被直线 l3,l4 所截,下列条件中,不能判断直线 l1∥l2 的是( B )
A.∠1=∠3B.∠5=∠4
C.∠5+∠3=180°D.∠4+∠2=180°
8.如图,AB∥CD 的条件是( D )
A.∠B=∠D
B.∠B+∠D=90°
C.∠B+∠D+∠E=180°
D.∠B+∠D=∠E
二、填空题(每小题 5 分,共 10 分)
9.如图,直线 AB,CD,EF 交于一点 O,OG⊥EF,且∠GOB=30°,∠AOC=40°,
则∠COE=__20°__.
第 9 题图
第 10 题图
10.如图,(1)如果∠1=__∠C__,那么 DE∥AC;
(2)如果∠1=__∠DEF__,那么 EF∥BC;
(3)如果∠FED+__∠EFC__=180°,那么 AC∥ED;
(4)如果∠2+__∠AED__=180°,那么 AB∥DF.
三、解答题(共 50 分)
11.(8 分)如图,由 A 地去 B 地再到河边 l 的最短线路是什么?请你画出并说明理由.
解:连接 AB,过点 B 作 BC⊥l 于 C 点,折线 ABC 即为所求,理由:①两点之间线段
最短,②垂线段最短.图略
12.(8 分)如图,直线 AB 和 CD 相交于点 O,OE⊥CD 于点 O,OD 平分∠BOF,∠BOE
=50°,求∠AOC,∠EOF,∠AOF 的度数.
解:∠AOC=40°,∠EOF=130°,∠AOF=100°
13.(10 分)如图,直线 AB,CD 相交于点 O,OE 平分∠BOD,OF 平分∠COE,∠2=
4∠1,求∠AOF 的度数.
解:由∠2+∠BOD=180°,OE 平分∠BOD,得 4∠1+2∠1=180°,∴∠1=30°,
∠AOC=∠BOD=60°,∠COF=1
2
∠COE=1
2(180°-∠DOE)=1
2(180°-30°)=75°,∴
∠AOF=60°+75°=135°
14.(12 分)如图,已知∠B=∠C,∠1=∠D,试问 OM∥AB 吗?为什么?
解:OM∥AB.理由:∵∠B=∠C,∴AB∥CD,又∵∠1=∠D,∴CD∥OM,∴AB∥
OM
15.(12 分)如图所示,直线 AB 与 CD 相交于点 O,OE⊥CD.
(1)若∠BOD=28°,求∠AOE 的度数;
(2)若 OF 平分∠AOC,小明经探究发现:当∠BOD 为锐角时,∠EOF 的度数始终都是
∠BOC 度数的一半,请你判断他的发现是否正确,并说明理由.
解:(1)∵∠BOD=28°,
∴∠AOC=∠BOD=28°.
∵OE⊥CD,
∴∠AOE=∠EOC-∠AOC=90°-28°=62°
(2)他的发现正确,理由如下:
设∠BOD=x,则∠AOC=∠BOD=x,∠BOC=180°-x.
∵OF 平分∠AOC,
∴∠FOC=1
2x.
∴∠EOF=∠EOC-∠FOC=90°-1
2x.
∴∠EOF=1
2
∠BOC
相关文档
- 人教版教学311生物必修3课堂教学—2021-10-1138页
- 广东省肇庆市实验中学2016届高三政2021-09-062页
- 广东省肇庆市实验中学2016届高三政2021-09-044页
- 广东省肇庆市实验中学2016届高三政2021-09-048页
- 广东省肇庆市实验中学2016届高三政2021-09-042页
- 广东省肇庆市实验中学2016届高三政2021-09-0411页
- 广东省肇庆市实验中学2016届高三政2021-09-045页
- 广东省肇庆市实验中学2016届高三政2021-09-043页
- 广东省肇庆市实验中学2016届高三政2021-09-044页
- 广东省肇庆市实验中学2016届高三政2021-09-046页