七年级下数学课件第一章二元一次方程组解法加减法（一）共18张幻灯片_鲁教版 18页

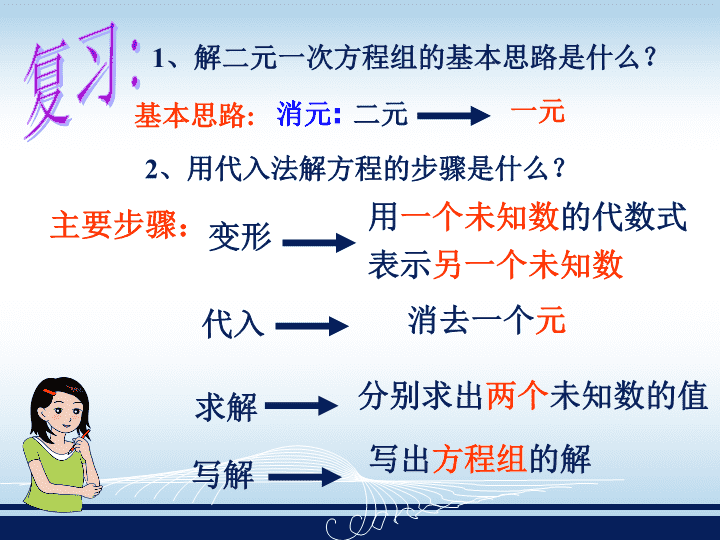
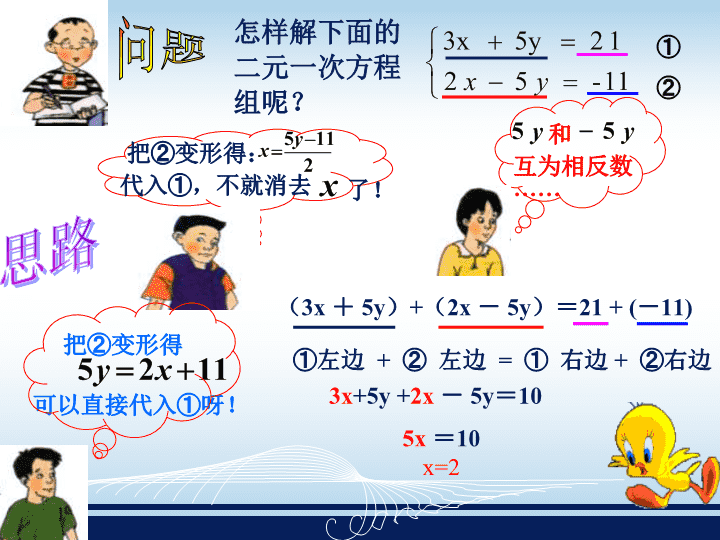
本节内容 1.2 ——加减消元法(一） 数学七年级（下） 1、解二元一次方程组的基本思路是什么？ 基本思路: 消元: 二元 一元 2、用代入法解方程的步骤是什么？ 主要步骤： 变形 代入 求解 写解 用一个未知数的代数式 表示另一个未知数 消去一个 元 分别求出两个未知数的值 写出方程组的解 怎样解下面的 二元一次方程 组呢？      11-52 125y3x yx ① ② 把②变形得： 2 115  yx 代入①，不就消去 x 了！ 可以直接代入①呀！ 把②变形得 1125  xy 和y5 y5 互为相反 数…… （3x ＋ 5y）+（2x － 5y）＝21 + (－11) ①左边 + ② 左边 = ① 右边 + ②右边 3x+5y +2x － 5y＝10 5x ＝10 x=2 所以原方程组的解是      2 3x y      11-52 125y3x yx ① ② 解:由①+②得: 5x=10 把x＝2代入①，得 3*2+5y=21 x＝2 y＝3 说一说 如何解下述二元一次方程组？     2 5 =9 2 3 =17 x+ y x y ① ② ， . - 从②得， ， 再代入①，得 这就把x消去了！ 3 17= 2 y+x          3 172 +5 = 9 2 y+ y 她得到的y的方程也就是 (3y+17)+5y=9 这不就可以直接从②得， 2x=3y+17， 然后把它代入①吗？ 方程①和②中都有2x， 为了消去x，干脆把方程①减 去方程②就可以了！ ①-②，得 8y= -8， 解得 y= -1 把y=-1代入①，得 2x+5(-1)=9， 解得 x= 7 因此原方程组的解是    2 5 =9 2 3 =17 x+ y x y ， ① . ②-    = 7 = 1 x y ， . - 参考以上思路，怎样解下面的二元一次 方程组呢？ 观察方程组中的两个方程，未知数x的系数相等，都是2．把 这两个方程两边分别相减，就可以消去未知数x，同样得到一 个一元一次方程．      132 75y2x yx ① ② 分析： 解：把 ②－①得:8y＝－8 y＝－1 把y ＝－1代入①，得 2x－5╳（－1）＝7 解得:x＝1 所以原方程组的解是      1 1x y 例3 解方程组： 举 例        7 3 = 1 2 3 = 8 x+ y x y ① ② , . - 两个方程中的未 知数y的系数互为相反 数，可以消去y. 解 ①+② ，得 9x = 9. 7x+3y+(2x-3y)=1+8 解得 x = 1 把x=1代入① ，得 7×1+3y = 1 解得 y = -2 因此原方程组的解是      = 1 = 2 x y , .- 说一说 在上面的方程组中，把方程①减去②，或者把方程① 与②相加，便消去了一个未知数。 被消去的未 知数系数相等或 互为相反数. 上面四个方程组中，是如何消去一个未知数的？ 消去一个未知数的方法是：如果两个方 程中有一个未知数的系数相等(或互为相反 数)，那么把这两个方程相减(或相加)； 被消去的未知数的系数有什么特点？ 结论 这种解二元一次方程组的方法叫 做加减消元法，简称加减法. 练习 用加减消元法解下列方程组：      2 = 21 2 3 =18 x+ y x+ y , ① ② ） - - （ 解: ①+② ，得 4y=16 解得 y=4 把y=4代入①，得 2x+4=-2 解得 x=-3 因此原方程组的解是      = 3 = 4 x y , . -      5 2 = 112 5 +3 = 4 x y x y , ） ① ② - - （      = 1 = 3 x y , .- 解: ①-② ，得 -5y=15 解得 y=-3 把y=-3代入①，得 5x-2×(-3)=11 解得 x=1 因此原方程组的解是          35= 4 81= 8 x y , .- 解: ①+② ，得 8x=70 353 2 6 4 y = × + 35= 4 x解得 35= 4 x把 代入①，得 81= 8 y -解得 因此原方程组的解是 623  yx 6425  yx (3) ① ② 分别相加 y 1.已知方程组 x+3y=17 2x-3y=6 两个方程 就可以消去未知数 分别相减 2.已知方程组 25x-7y=16 25x+6y=10 两个方程 就可以消去未知数 x 一.填空题： 只要两边 只要两边 二.选择题 1. 用加减法解方程组 6x+7y=-19① 6x-5y=17② 应用（ ） A.①-②消去y B.①-②消去x B. ②- ①消去常数项 D. 以上都不对 B 2.方程组 3x+2y=13 3x-2y=5 消去y后所得的方程是（ ）B A.6x=8 B.6x=18 C.6x=5 D.x=18 三、指出下列方程组求解过程 中有错误步骤，并给予订正： 7x－4y＝4 5x－4y＝－4 解:①－②，得 　　2x＝4－4， 　　　x＝0 ① ① ② ② 3x－4y＝14 5x＋4y＝2 解　①－②，得 　　－2x＝12 　　　x ＝－6 解:　①－②，得 　　2x＝4＋4， 　　　x＝4 解:　①＋②，得 　　8x＝16 　　　x ＝2 1、已知a、b满足方程组 a+2b=8 2a+b=7 则a+b= 5 点击中考 2、方程组 的解是 （ ）    3 =4 2 3 = 1 x+ y x y ， - -             = 1 =1 = 2 = 2A B C D= 1 =1 =2 = 1 x x x x. . . . y y y y - - - - - 解析    3 =4 2 3 = 1 x+ y x y ， ① ②- - ①+②得 3x = 3， x=1 把x=1代入①得 y = 1,    =1 =1 . x y ， 所以原方程组的解为 故选B. B 上面这些方程组的特点是什么? 解这类方程组基本思路是什么？ 主要步骤有哪些？ 主要步骤： 特点: 基本思路: 写解 求解 加减 二元 一元加减消元: 消去一个元 分别求出两个未知数的值 写出原方程组的解 同一个未知数的系数相同或互为相反数 主要步骤： 基本思路: 写解 求解 加减 二元 一元加减消元: 消去一个元 求出两个未知数的值 写出方程组的解 小结 ： 1.加减消元法解方程组基本思路是什么？ 主要步骤有哪些？ 变形 同一个未知数的系 数相同或互为相反数 2. 二元一次方程组解法有 .代入法、加减法