2019-2020学年山东省济南市历城区七年级（上）期末数学试卷 9页

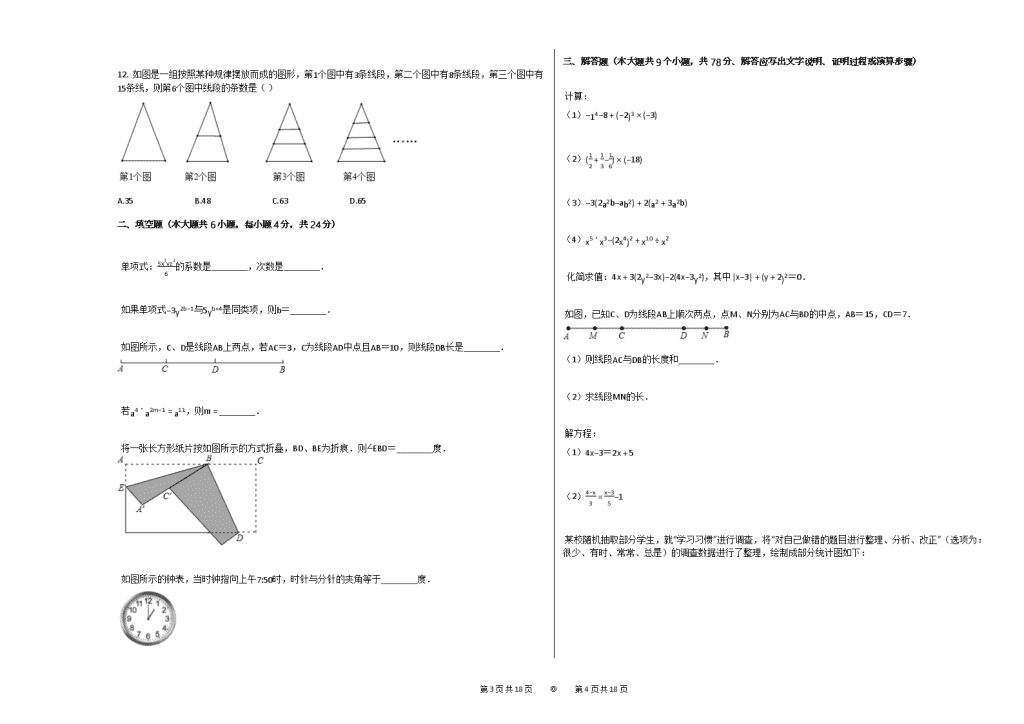
‎2019-2020学年山东省济南市历城区七年级（上）期末数学试卷 一、遗规了（本大量共12小题，每小题4分，共很分．每小题只活 ‎ ‎ ‎1. ‎−2020‎的绝对值是‎(‎        ‎)‎ ‎ A.‎−2020‎ B.‎2020‎ C.‎−‎‎1‎‎2020‎ D.‎‎1‎‎2020‎ ‎ ‎ ‎2. 一个几何体由大小相同的小立方块搭成，从上面看到的几何体形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看这个几何体得到的形状图是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎3. 某种细胞的平均直径只有‎0.00007‎米，用科学记数法表示此数应该是（ ） ‎ A.‎7.0×‎‎10‎‎4‎ B.‎7.0×‎‎10‎‎−5‎ C.‎0.7×‎‎10‎‎6‎ D.‎‎0.7×‎‎10‎‎−4‎ ‎ ‎ ‎4. 下面调查统计中，适合采用普查方式的是（ ） ‎ A.华为手机的市场占有率 B.乘坐飞机的旅客是否携带了违禁物品 C.国家宝藏”专栏电视节目的收视率 D.“现代”汽车每百公里的耗油量 ‎ ‎ ‎5. 下列计算正确的是（ ） ‎ A.a⋅‎a‎2‎＝a‎2‎ B.a‎2‎‎+‎a‎4‎＝a‎8‎ C.‎(ab‎)‎‎3‎＝ab‎3‎ D.a‎3‎‎÷a＝‎a‎2‎ ‎ ‎ ‎6. 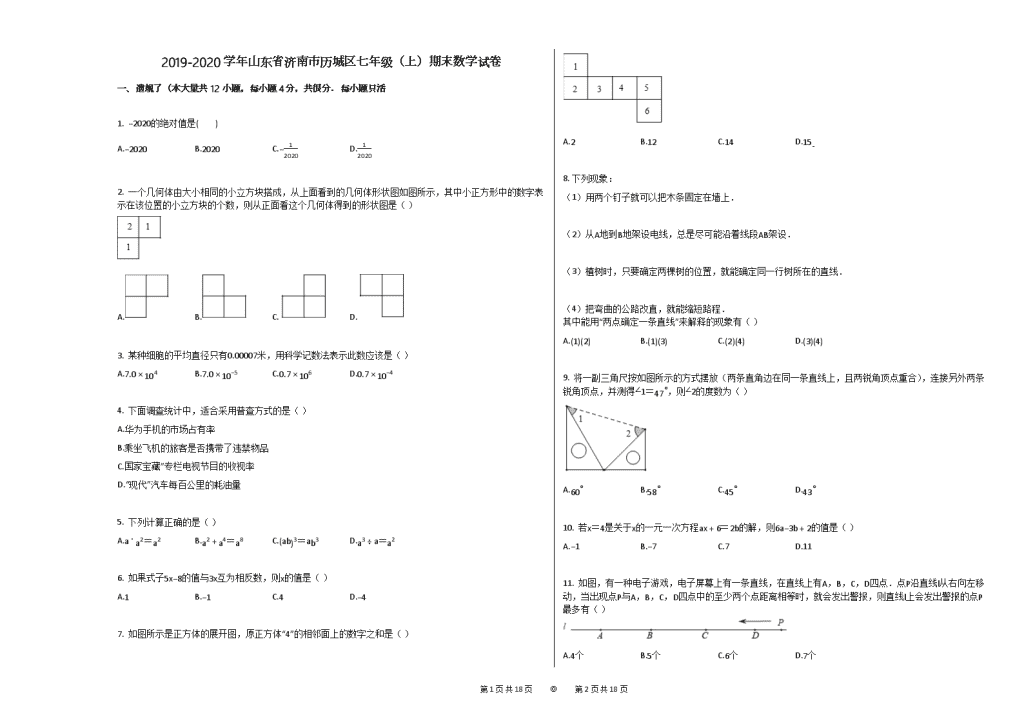如果式子‎5x−8‎的值与‎3x互为相反数，则x的值是（ ） ‎ A.‎1‎ B.‎−1‎ C.‎4‎ D.‎‎−4‎ ‎ ‎ ‎7. 如图所示是正方体的展开图，原正方体“‎4‎”的相邻面上的数字之和是（ ） ‎ A.‎2‎ B.‎12‎ C.‎14‎ D.‎15‎ ‎ ‎ ‎ ‎8. 下列现象： ‎ ‎（1）用两个钉子就可以把木条固定在墙上．‎ ‎ ‎ ‎（2）从A地到B地架设电线，总是尽可能沿着线段AB架设．‎ ‎ ‎ ‎（3）植树时，只要确定两棵树的位置，就能确定同一行树所在的直线．‎ ‎ ‎ ‎（4）把弯曲的公路改直，就能缩短路程． 其中能用“两点确定一条直线”来解释的现象有（ ）‎ A.‎(1)(2)‎ B.‎(1)(3)‎ C.‎(2)(4)‎ D.‎‎(3)(4)‎ ‎ ‎ ‎9. 将一副三角尺按如图所示的方式摆放（两条直角边在同一条直线上，且两锐角顶点重合），连接另外两条锐角顶点，并测得‎∠1‎＝‎47‎‎∘‎，则‎∠2‎的度数为（ ） ‎ A.‎60‎‎∘‎ B.‎58‎‎∘‎ C.‎45‎‎∘‎ D.‎‎43‎‎∘‎ ‎ ‎ ‎10. 若x＝‎4‎是关于x的一元一次方程ax+6‎＝‎2b的解，则‎6a−3b+2‎的值是（ ） ‎ A.‎−1‎ B.‎−7‎ C.‎7‎ D.‎‎11‎ ‎ ‎ ‎11. 如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点．点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P最多有（ ） ‎ A.‎4‎个 B.‎5‎个 C.‎6‎个 D.‎7‎个 第17页 共18页 ◎ 第18页 共18页 ‎ ‎ ‎12. 如图是一组按照某种规律摆放而成的图形，第‎1‎个图中有‎3‎条线段，第二个图中有‎8‎条线段，第三个图中有‎15‎条线，则第‎6‎个图中线段的条数是（ ） ‎ A.‎35‎ B.‎48‎ C.‎63‎ D.‎‎65‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎ ‎ ‎ 单项式：‎5x‎3‎yz‎2‎‎6‎的系数是________，次数是________． ‎ ‎ ‎ ‎ 如果单项式‎−3‎y‎2b−1‎与‎5‎yb+4‎是同类项，则b＝________． ‎ ‎ ‎ ‎ 如图所示，C、D是线段AB上两点，若AC＝‎3‎，C为线段AD中点且AB＝‎10‎，则线段DB长是________． ‎ ‎ ‎ ‎ 若a‎4‎‎⋅a‎2m−1‎=‎a‎11‎，则m=‎________． ‎ ‎ ‎ ‎ 将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕．则‎∠EBD＝________度． ‎ ‎ ‎ ‎ 如图所示的钟表，当时钟指向上午‎7:50‎时，时针与分针的夹角等于________度． ‎ 三、解答题（本大题共9个小题，共78分、解答应写出文字说明、证明过程或演算步骤）‎ ‎ ‎ ‎ 计算： ‎ ‎（1）‎‎−‎1‎‎4‎−8+(−2‎)‎‎3‎×(−3)‎ ‎ ‎ ‎（2）‎‎(‎1‎‎2‎+‎1‎‎3‎−‎1‎‎6‎)×(−18)‎ ‎ ‎ ‎（3）‎‎−3(2a‎2‎b−ab‎2‎)+2(a‎2‎+3a‎2‎b)‎ ‎ ‎ ‎（4）‎x‎5‎‎⋅x‎3‎−(2x‎4‎‎)‎‎2‎+x‎10‎÷‎x‎2‎ ‎ ‎ ‎ 化简求值：‎4x+3(2y‎2‎−3x)−2(4x−3y‎2‎)‎，其中‎|x−3|+(y+2‎‎)‎‎2‎＝‎0‎． ‎ ‎ ‎ ‎ 如图，已知C、D为线段AB上顺次两点，点M、N分别为AC与BD的中点，AB＝‎15‎，CD＝‎7‎． ‎ ‎（1）则线段AC与DB的长度和________．‎ ‎ ‎ ‎（2）求线段MN的长．‎ ‎ ‎ ‎ 解方程： ‎ ‎（1）‎4x−3‎＝‎‎2x+5‎ ‎ ‎ ‎（2）‎‎4−x‎3‎‎=x−3‎‎5‎−1‎ ‎ ‎ ‎ 某校随机抽取部分学生，就“学习习惯”进行调查，将“对自己做错的题目进行整理、分析、改正”（选项为：很少、有时、常常、总是）的调查数据进行了整理，绘制成部分统计图如下： ‎ 第17页 共18页 ◎ 第18页 共18页 ‎ 请根据图中信息，解答下列问题 ‎ ‎（1）该调查的样本容量为________，a＝________‎%‎，b＝________‎%‎，“常常”对应扇形的圆心角为________‎‎​‎‎∘‎ ‎ ‎ ‎（2）请你补全条形统计图；‎ ‎ ‎ ‎（3）若该校共有‎3200‎名学生，请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名？‎ ‎ ‎ ‎ 学校要购入两种记录本，其中A种记录本每本‎3‎元，B种记录本每本‎2‎元，且购买A种记录本的数量比B种记录本的‎2‎倍还多‎20‎本，总花费为‎460‎元． ‎ ‎（1）求购买B种记录本的数量；‎ ‎ ‎ ‎（2）某商店搞促销活动，A种记录本按‎8‎折销售，B种记录本按‎9‎折销售，则学校此次可以节省多少钱？‎ ‎ ‎ ‎ 如图，将三个边长都为a的正方形一个顶点重合放置． ‎ ‎（1）若‎∠l＝‎50‎‎∘‎，‎∠2‎＝‎15‎‎∘‎，则‎∠3‎＝________度；‎ ‎ ‎ ‎（2）判断：‎∠1+∠2+∠3‎＝________度，并说明理由．‎ ‎ ‎ ‎ 小明练习跳绳．以‎1‎分钟跳‎165‎个为目标，并把‎20‎次‎1‎分钟跳绳的数量记录如表（超过‎165‎个的部分记为“+”，少于‎165‎个的部分记为“-”） ‎ 与目标数量的差依（单位：个）‎ ‎−11‎ ‎−6‎ ‎−2‎ ‎+4‎ ‎+10‎ 次数 ‎4‎ ‎5‎ ‎3‎ ‎6‎ ‎2‎ ‎ ‎ ‎（1）小明在这‎20‎次跳绳练习中，‎1‎分钟最多跳多少个？‎ ‎ ‎ ‎（2）小明在这‎20‎次跳绳练习中，‎1‎分钟跳绳个数最多的一次比最少的一次多几个？‎ ‎ ‎ ‎（3）小明在这‎20‎次跳绳练习中，累计跳绳多少个？‎ ‎ ‎ ‎ 已知直线AB和CD交于O，‎∠AOC的度数为x，‎∠BOE＝‎90‎‎∘‎，OF平分‎∠AOD． ‎ ‎（1）当x＝‎20‎‎∘‎时，则‎∠EOC＝________度；‎∠FOD＝________度．‎ ‎ ‎ ‎（2）当x＝‎60‎‎∘‎时，射线OE′‎从OE开始以‎10‎‎∘‎‎/‎秒的速度绕点O逆时针转动，同时射线OF′‎从OF开始以‎8‎‎∘‎‎/‎秒的速度绕点O顺时针转动，当射线OE′‎转动一周时射线OF′‎也停止转动，求至少经过多少秒射线OE′‎与射线OF′‎重合？‎ ‎ ‎ ‎（3）在（2）的条件下，射线OE′‎在转动一周的过程中，当‎∠E′OF′‎＝‎90‎‎∘‎时，请直接写出射线OE′‎转动的时间．‎ 第17页 共18页 ◎ 第18页 共18页 参考答案与试题解析 ‎2019-2020学年山东省济南市历城区七年级（上）期末数学试卷 一、遗规了（本大量共12小题，每小题4分，共很分．每小题只活 ‎1.‎ ‎【答案】‎ B ‎【考点】‎ 绝对值 ‎【解析】‎ 根据绝对值的定义直接进行计算．‎ ‎【解答】‎ 解：根据绝对值的概念可知： ‎|−2020|‎‎=2020‎. 故选B.‎ ‎2.‎ ‎【答案】‎ B ‎【考点】‎ 由三视图判断几何体 简单组合体的三视图 ‎【解析】‎ 从正面看，注意“长对正，宽相等、高平齐”，根据所放置的小立方体的个数画出图形即可．‎ ‎【解答】‎ 从正面看所得到的图形为：‎B ‎3.‎ ‎【答案】‎ B ‎【考点】‎ 科学记数法--表示较小的数 科学记数法--表示较大的数 ‎【解析】‎ 绝对值小于‎1‎的正数也可以利用科学记数法表示，一般形式为a×‎‎10‎‎−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的‎0‎的个数所决定．‎ ‎【解答】‎ ‎0.00007‎米，用科学记数法表示此数应该是‎7.0×‎‎10‎‎−5‎．‎ ‎4.‎ ‎【答案】‎ B ‎【考点】‎ 全面调查与抽样调查 ‎【解析】‎ 根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似判断即可．‎ ‎【解答】‎ A‎、对华为手机的市场占有率的调查范围广，适合抽样调查，故此选项不符合题意； B、对乘坐飞机的旅客是否携带了违禁物品的调查情况适合普查，故此选项符合题意； C、对国家宝藏”专栏电视节目的收视率的调查范围广，适合抽样调查，故此选项不符合题意； D、对“现代”汽车每百公里的耗油量的调查范围广适合抽样调查，故此选项不符合题意；‎ ‎5.‎ ‎【答案】‎ D ‎【考点】‎ 同底数幂的除法 同底数幂的乘法 合并同类项 幂的乘方与积的乘方 ‎【解析】‎ 分别根据同底数幂的乘法法则，合并同类项的法则，积的乘方以及同底数幂的除法法则逐一判断即可．‎ ‎【解答】‎ a‎2‎与a‎4‎不是同类项，所以不能合并，故选项B不合题意‎(1)(ab‎)‎‎3‎＝a‎3‎b‎3‎，故选项C不合题意（2）a‎3‎‎÷a＝a‎2‎，正确，故选项D符合题意． 故选：D．‎ ‎6.‎ ‎【答案】‎ A ‎【考点】‎ 列代数式求值 解一元一次方程 ‎【解析】‎ 利用相反数的性质列出方程，求出方程的解即可得到x的值．‎ ‎【解答】‎ 根据题意得：‎5x−8+3x＝‎0‎， 移项合并得：‎8x＝‎8‎， 解得：x＝‎1‎，‎ ‎7.‎ ‎【答案】‎ D ‎【考点】‎ 正方体相对两个面上的文字 ‎【解析】‎ 根据正方体的展开图，原正方体“‎4‎”的相对面上的数字为‎2‎，即可得到原正方体“‎4‎”的相邻面上的数字分别为‎1‎，‎3‎，‎5‎，‎6‎，进而得出结论．‎ ‎【解答】‎ ‎∵ 正方体的展开图，原正方体“‎4‎”的相对面上的数字为‎2‎， ∴ 原正方体“‎4‎”的相邻面上的数字分别为‎1‎，‎3‎，‎5‎，‎6‎， ‎ 第17页 共18页 ◎ 第18页 共18页 ‎∴ 原正方体“‎4‎”的相邻面上的数字之和是‎15‎，‎ ‎8.‎ ‎【答案】‎ 用两个钉子就可以把木条固定在墙上，根据是两点确定一条直线；‎ 从A地到B地架设电线，总是尽可能沿着线段AB架设，根据是两点之间线段最短；‎ 植树时，只要确定两棵树的位置，就能确定同一行树所在的直线，根据是两点确定一条直线；‎ B ‎【考点】‎ 直线的性质：两点确定一条直线 ‎【解析】‎ 直接利用直线的性质以及两点之间线段最短分析得出答案．‎ ‎【解答】‎ 用两个钉子就可以把木条固定在墙上，根据是两点确定一条直线；‎ 从A地到B地架设电线，总是尽可能沿着线段AB架设，根据是两点之间线段最短；‎ 植树时，只要确定两棵树的位置，就能确定同一行树所在的直线，根据是两点确定一条直线；‎ 把弯曲的公路改直，就能缩短路程，根据是两点之间线段最短． 故选：B．‎ ‎9.‎ ‎【答案】‎ B ‎【考点】‎ 角的计算 ‎【解析】‎ 由三角尺角的特殊性，利用平角定义及三角形内角和定理即可求出．‎ ‎【解答】‎ 如图所示， ‎∠3‎＝‎180‎‎∘‎‎−‎60‎‎∘‎−‎‎45‎‎∘‎＝‎75‎‎∘‎， 则‎∠2‎＝‎180‎‎∘‎‎−∠1−∠3‎＝‎180‎‎∘‎‎−‎47‎‎∘‎−‎‎75‎‎∘‎＝‎58‎‎∘‎．‎ ‎10.‎ ‎【答案】‎ B ‎【考点】‎ 一元一次方程的解 ‎【解析】‎ 将x＝‎4‎代入方程中得到等式‎4a+6‎＝‎2b，移项后并整理得到‎2a−b＝‎−3‎，其中a和b的系数比是‎2:−1‎，代数式‎6a−3b+2‎中a和b的系数比也是‎2:−1‎，由此可以将代数式化成‎3(2a−b)+2‎．‎ ‎【解答】‎ 将x＝‎4‎代入方程得：‎4a+6‎＝‎2b， 整理得：‎2a−b＝‎−3‎， 等式两边同时乘以‎3‎，得：‎6a−3b＝‎−9‎， 则‎6a−3b+2‎＝‎−9+2‎＝‎−7‎，‎ ‎11.‎ ‎【答案】‎ B ‎【考点】‎ 两点间的距离 ‎【解析】‎ 点P与A，B，C，D四点中的至少两个点距离相等时，也就是点P恰好是其中一条线段中点．而图中共有线段六条，所以出现报警次数最多‎5‎次．‎ ‎【解答】‎ 由题意知，当P点经过任意一条线段中点的时候会发出警报 ∵ 图中共有线段DC、DB、DA、CB、CA、BA ∴ 发出警报的可能最多有‎5‎个 ‎12.‎ ‎【答案】‎ B ‎【考点】‎ 规律型：图形的变化类 规律型：点的坐标 规律型：数字的变化类 ‎【解析】‎ 根据题目中的图形，可以发现各个图形中线段条数的变化规律，从而可以解答本题．‎ ‎【解答】‎ 由图可得， 第‎1‎个图形中有：‎3‎条线段， 第‎2‎个图形中有：‎3+3+2‎＝‎3×2+2×1‎＝‎8‎条线段， 第‎3‎个图形中有：‎3+3+3+2+2+2‎＝‎3×3+2×3‎＝‎15‎条线段， 第‎4‎个图形中有：‎3+3+3+3+2+2+2+2+2+2‎＝‎3×4+2×6‎＝‎24‎条线段， …， 则第n个图形中有：‎[(n+1‎)‎‎2‎−1]‎条线段， ∴ 当n＝‎6‎时，‎[(n+1‎)‎‎2‎−1]‎＝‎[(6+1‎)‎‎2‎−1]‎＝‎48‎，‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎【答案】‎ ‎5‎‎6‎‎,‎‎6‎ ‎【考点】‎ 单项式的概念的应用 ‎【解析】‎ 直接利用单项式的次数与系数确定方法分析得出答案．‎ ‎【解答】‎ 单项式：‎5x‎3‎yz‎2‎‎6‎的系数是：‎5‎‎6‎，次数是：‎6‎．‎ ‎【答案】‎ ‎5‎ ‎【考点】‎ 同类项的概念 第17页 共18页 ◎ 第18页 共18页 ‎【解析】‎ 根据同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，可得答案．注意同类项与字母的顺序无关，与系数无关．‎ ‎【解答】‎ 由同类项的定义可知‎2b−1‎＝b+4‎， 解得b＝‎5‎，‎ ‎【答案】‎ ‎4‎ ‎【考点】‎ 两点间的距离 ‎【解析】‎ 由已知中点可求AD＝‎6‎，再由AB＝‎10‎即可求BD．‎ ‎【解答】‎ ‎∵ AC＝‎3‎，C为线段AD中点， ∴ CD＝‎3‎， ∴ AD＝‎6‎， ∵ AB＝‎10‎， ∴ BD＝‎4‎；‎ ‎【答案】‎ ‎4‎ ‎【考点】‎ 同底数幂的乘法 ‎【解析】‎ 根据同底数幂的乘法法则解答即可．‎ ‎【解答】‎ 解：∵ a‎4‎‎⋅a‎2m−1‎=‎a‎11‎， ∴ ‎4+(2m−1)=‎‎11‎，解得：m=‎‎4‎． 故答案为：‎4‎.‎ ‎【答案】‎ ‎90‎ ‎【考点】‎ 角的计算 ‎【解析】‎ 根据翻折的性质可知，‎∠ABE＝‎∠A′BE，‎∠DBC＝‎∠DBC′‎，又∵ ‎∠ABE+∠A′BE+∠DBC+∠DBC′‎＝‎180‎‎∘‎，且‎∠EBD＝‎∠A′BE+∠DBC′‎，继而即可求出答案．‎ ‎【解答】‎ 根据翻折的性质可知，‎∠ABE＝‎∠A′BE，‎∠DBC＝‎∠DBC′‎， 又∵ ‎∠ABE+∠A′BE+∠DBC+∠DBC′‎＝‎180‎‎∘‎， ∴ ‎∠EBD＝‎∠A′BE+∠DBC′‎＝‎180‎‎∘‎‎×‎1‎‎2‎=‎‎90‎‎∘‎．‎ ‎【答案】‎ ‎65‎ ‎【考点】‎ 钟面角 ‎【解析】‎ 根据钟面平均分成‎12‎份，可得每份的度数，根据时针与分针相距的份数乘以每份的度数，可得答案．‎ ‎【解答】‎ 当时钟指向上午‎7:50‎时，时针与分针相距‎2+‎10‎‎60‎=‎‎13‎‎6‎（份）， 当时钟指向上午‎7:50‎时，时针与分针的夹角‎30‎‎∘‎‎×‎13‎‎6‎=‎‎65‎‎∘‎，‎ 三、解答题（本大题共9个小题，共78分、解答应写出文字说明、证明过程或演算步骤）‎ ‎【答案】‎ ‎−‎1‎‎4‎−8+(−2‎)‎‎3‎×(−3)‎‎ ＝‎−1−8+(−8)×(−3)‎ ＝‎−9+24‎ ＝‎‎15‎ ‎(‎1‎‎2‎+‎1‎‎3‎−‎1‎‎6‎)×(−18)‎‎ ‎=‎1‎‎2‎×(−18)+‎1‎‎3‎×(−18)−‎1‎‎6‎×(−18)‎ ＝‎−9−6+3‎ ＝‎‎−12‎ ‎−3(2a‎2‎b−ab‎2‎)+2(a‎2‎+3a‎2‎b)‎‎ ＝‎−6a‎2‎b+3ab‎2‎+2a‎2‎+6a‎2‎b ＝‎‎3ab‎2‎+2a x‎5‎‎⋅x‎3‎−(2x‎4‎‎)‎‎2‎+x‎10‎÷‎x‎2‎‎ ＝x‎8‎‎−4x‎8‎+‎x‎8‎ ＝‎−2‎x‎8‎．‎ ‎【考点】‎ 整式的加减 幂的乘方与积的乘方 同底数幂的乘法 有理数的混合运算 同底数幂的除法 ‎【解析】‎ ‎（1）按有理数的混合运算顺序运算即可； （2）利用乘法对加法的分配律，能使运算简便； （3）先去括号，再合并同类项； （4）按整式混合运算的步骤运算得结论．‎ ‎【解答】‎ ‎−‎1‎‎4‎−8+(−2‎)‎‎3‎×(−3)‎‎ ＝‎−1−8+(−8)×(−3)‎ ＝‎−9+24‎ ＝‎‎15‎ ‎(‎1‎‎2‎+‎1‎‎3‎−‎1‎‎6‎)×(−18)‎‎ ‎=‎1‎‎2‎×(−18)+‎1‎‎3‎×(−18)−‎1‎‎6‎×(−18)‎ ‎ 第17页 共18页 ◎ 第18页 共18页 ‎＝‎−9−6+3‎ ＝‎‎−12‎ ‎−3(2a‎2‎b−ab‎2‎)+2(a‎2‎+3a‎2‎b)‎‎ ＝‎−6a‎2‎b+3ab‎2‎+2a‎2‎+6a‎2‎b ＝‎‎3ab‎2‎+2a x‎5‎‎⋅x‎3‎−(2x‎4‎‎)‎‎2‎+x‎10‎÷‎x‎2‎‎ ＝x‎8‎‎−4x‎8‎+‎x‎8‎ ＝‎−2‎x‎8‎．‎ ‎【答案】‎ 原式＝‎4x+6y‎2‎−9x−8x+6‎y‎2‎＝‎12y‎2‎−13x， 因为‎|x−3|+(y+2‎‎)‎‎2‎＝‎0‎， 所以x＝‎3‎，y＝‎−2‎， 则原式＝‎12×4−39‎＝‎48−39‎＝‎9‎．‎ ‎【考点】‎ 非负数的性质：算术平方根 非负数的性质：绝对值 整式的加减--化简求值 非负数的性质：偶次方 ‎【解析】‎ 原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．‎ ‎【解答】‎ 原式＝‎4x+6y‎2‎−9x−8x+6‎y‎2‎＝‎12y‎2‎−13x， 因为‎|x−3|+(y+2‎‎)‎‎2‎＝‎0‎， 所以x＝‎3‎，y＝‎−2‎， 则原式＝‎12×4−39‎＝‎48−39‎＝‎9‎．‎ ‎【答案】‎ ‎8‎ MN‎＝CM+CD+DN ‎=‎1‎‎2‎AC+‎1‎‎2‎BD+CD ‎=‎1‎‎2‎(AC+BD)+CD ‎=‎1‎‎2‎(AB−CD)+CD ‎=‎1‎‎2‎AB+‎1‎‎2‎CD ＝‎11‎．‎ ‎【考点】‎ 两点间的距离 ‎【解析】‎ ‎（1）根据线段间关系可得而的：AC+BD＝AB−CD＝‎15‎＝‎7‎＝‎8‎； （2）由MN＝CM+CD+DN=‎1‎‎2‎AB+‎1‎‎2‎CD，将已知代入即可．‎ ‎【解答】‎ AC+BD‎＝AB−CD＝‎15‎＝‎7‎＝‎8‎， 故答案为‎8‎；‎ MN‎＝CM+CD+DN ‎=‎1‎‎2‎AC+‎1‎‎2‎BD+CD ‎=‎1‎‎2‎(AC+BD)+CD ‎=‎1‎‎2‎(AB−CD)+CD ‎=‎1‎‎2‎AB+‎1‎‎2‎CD ＝‎11‎．‎ ‎【答案】‎ 移项合并得：‎2x＝‎8‎， 解得：x＝‎4‎；‎ 去分母得：‎20−5x＝‎3x−9−15‎， 移项合并得：‎−8x＝‎−44‎， 解得：x＝‎5.5‎．‎ ‎【考点】‎ 解一元一次方程 ‎【解析】‎ ‎（1）方程移项合并，把x系数化为‎1‎，即可求出解； （2）方程去分母，去括号，移项合并，把x系数化为‎1‎，即可求出解．‎ ‎【解答】‎ 移项合并得：‎2x＝‎8‎， 解得：x＝‎4‎；‎ 去分母得：‎20−5x＝‎3x−9−15‎， 移项合并得：‎−8x＝‎−44‎， 解得：x＝‎5.5‎．‎ ‎【答案】‎ ‎200‎‎,‎12‎,‎36‎,‎‎108‎ ‎200×30%‎‎＝‎60‎（名） ．‎ ‎∵ ‎3200×36%‎＝‎1152‎（名） ∴ “总是”对错题进行整理、分析、改正的学生有‎1152‎名． 故答案为：‎200‎、‎12‎、‎36‎、‎108‎．‎ 第17页 共18页 ◎ 第18页 共18页 ‎【考点】‎ 条形统计图 总体、个体、样本、样本容量 扇形统计图 用样本估计总体 ‎【解析】‎ ‎（1）首先用“有时”对错题进行整理、分析、改正的学生的人数除以‎22%‎，求出该调查的样本容量为多少；然后分别用很少、总是“对自己做错的题目进行整理、分析、改正”的人数除以样本容量，求出a、b的值各是多少；最后根据“常常”对应的人数的百分比是‎30%‎，求出“常常”对应扇形的圆心角为多少即可． （2）求出常常“对自己做错的题目进行整理、分析、改正”的人数，补全条形统计图即可． （3）用该校学生的人数乘“总是”对错题进行整理、分析、改正的学生占的百分率即可．‎ ‎【解答】‎ ‎∵ ‎44÷22%‎＝‎200‎（名） ∴ 该调查的样本容量为‎200‎； a＝‎24÷200‎＝‎12%‎， b＝‎72÷200‎＝‎36%‎， “常常”对应扇形的圆心角为： ‎360‎‎∘‎‎×30%‎＝‎108‎‎∘‎．‎ ‎200×30%‎‎＝‎60‎（名） ．‎ ‎∵ ‎3200×36%‎＝‎1152‎（名） ∴ “总是”对错题进行整理、分析、改正的学生有‎1152‎名． 故答案为：‎200‎、‎12‎、‎36‎、‎108‎．‎ ‎【答案】‎ 购买A种记录本‎120‎本，B种记录本‎50‎本 学校此次可以节省‎82‎元钱 ‎【考点】‎ 一元一次方程的应用——其他问题 一元一次方程的应用——工程进度问题 ‎【解析】‎ ‎（1）设购买B种记录本x本，则购买A种记录表‎(2x+20)‎本，根据总价＝单价‎×‎数量，即可得出关于x的一元一次方程，解之即可得出结论； （2）根据节省的钱数＝原价-优惠后的价格，即可求出结论．‎ ‎【解答】‎ 设购买B种记录本x本，则购买A种记录表‎(2x+20)‎本， 依题意，得：‎3(2x+20)+2x＝‎460‎， 解得：x＝‎50‎， ∴ ‎2x+20‎＝‎120‎． 答：购买A种记录本‎120‎本，B种记录本‎50‎本．‎ ‎460−3×120×0.8−2×50×0.9‎‎＝‎82‎（元）． 答：学校此次可以节省‎82‎元钱．‎ ‎【答案】‎ ‎65‎ ‎90‎ ‎【考点】‎ 角的计算 ‎【解析】‎ 先根据同角的余角相等得：‎∠3‎＝‎∠4‎，最后由‎∠1+∠2+∠3‎＝‎90‎‎∘‎可得结论．‎ ‎【解答】‎ 如图： ∵ ‎∠1+∠4+∠2‎＝‎90‎‎∘‎， ∵ ‎∠l＝‎50‎‎∘‎，‎∠2‎＝‎15‎‎∘‎， ∴ ‎∠4‎＝‎25‎‎∘‎， 根据同角的余角相等得：‎∠3‎＝‎∠4‎＝‎65‎‎∘‎；‎ 根据同角的余角相等得：‎∠3‎＝‎∠4‎， ∵ ‎∠1+∠4+∠2‎＝‎90‎‎∘‎， ∴ ‎∠1+∠2+∠3‎＝‎90‎‎∘‎， 故答案为：‎65‎，‎90‎．‎ ‎【答案】‎ 小明在这‎20‎次跳绳练习中，‎1‎分钟最多跳‎175‎个 小明在这‎20‎次跳绳练习中，‎1‎分钟跳绳个数最多的一次比最少的一次多‎21‎个 小明在这‎20‎次跳绳练习中，累计跳绳‎3264‎个 ‎【考点】‎ 正数和负数的识别 ‎【解析】‎ ‎（1）用‎165‎加上超过的最大的数字‎+10‎，即可； （2）用超过的最大的数字‎+10‎，减去少于‎165‎最多的数字‎−11‎，即可； （3）先用‎165×20‎，再将超过和不足‎165‎的计算，两者相加即可．‎ ‎【解答】‎ 跳绳最多的一次为：‎165+10‎＝‎175‎（个） 答：小明在这‎20‎次跳绳练习中，‎1‎分钟最多跳‎175‎个．‎ ‎(+10)−(−11)‎‎＝‎10+11‎＝‎21‎（个） 答：小明在这‎20‎次跳绳练习中，‎1‎分钟跳绳个数最多的一次比最少的一次多‎21‎个．‎ 第17页 共18页 ◎ 第18页 共18页 ‎165×20−11×4−6×5−2×3+4×6+10×2‎‎＝‎3264‎（个） 答：小明在这‎20‎次跳绳练习中，累计跳绳‎3264‎个．‎ ‎【答案】‎ ‎70‎‎,‎‎80‎ 当射线OE‎′‎与射线OF‎′‎重合时至少需要‎25‎‎3‎秒；‎ 射线OE‎′‎转动的时间为‎10‎‎3‎秒或‎40‎‎3‎秒或‎70‎‎3‎秒或‎100‎‎3‎秒 ‎【考点】‎ 邻补角 对顶角 角平分线的定义 ‎【解析】‎ ‎（1）利用互余和互补的定义可得：‎∠EOC与‎∠FOD的度数． （2）先根据x＝‎60‎‎∘‎，求‎∠EOF＝‎150‎‎∘‎，则射线OE‎′‎、OF‎′‎第一次重合时，其OE‎′‎运动的度数‎+OF‎′‎运动的度数＝‎150‎，列式解出即可； （3）分两种情况：在直线OE的左边和右边，根据其夹角列‎4‎个方程可得时间．‎ ‎【解答】‎ ‎∵ ‎∠BOE＝‎90‎‎∘‎， ∴ ‎∠AOE＝‎90‎‎∘‎， ∵ ‎∠AOC＝x＝‎20‎‎∘‎， ∴ ‎∠EOC＝‎90‎‎∘‎‎−‎‎20‎‎∘‎＝‎70‎‎∘‎， ‎∠AOD＝‎180‎‎∘‎‎−‎‎20‎‎∘‎＝‎160‎‎∘‎， ∵ OF平分‎∠AOD， ∴ ‎∠FOD=‎1‎‎2‎∠AOD=‎1‎‎2‎×160=‎‎80‎‎∘‎； 故答案为：‎70‎，‎80‎；‎ 当x＝‎60‎‎∘‎，‎∠EOF＝‎90‎‎∘‎‎+‎‎60‎‎∘‎＝‎150‎‎∘‎ 设当射线OE‎′‎与射线OF‎′‎重合时至少需要t秒， ‎10t+8t＝‎150‎， t=‎‎25‎‎3‎， 答：当射线OE‎′‎与射线OF‎′‎重合时至少需要‎25‎‎3‎秒；‎ 设射线OE‎′‎转动的时间为t秒， 由题意得：‎10t+90+8t＝‎150‎或‎10t+8t＝‎150+90‎或‎360−10t＝‎8t−150+90‎或‎360−10t+360−8t+90‎＝‎360−150‎， t=‎‎10‎‎3‎或‎40‎‎3‎或‎70‎‎3‎或‎100‎‎3‎． 答：射线OE‎′‎转动的时间为‎10‎‎3‎秒或‎40‎‎3‎秒或‎70‎‎3‎秒或‎100‎‎3‎秒．‎ 第17页 共18页 ◎ 第18页 共18页