人教版七年级上册数学课时跟踪训练：第一章 有理数 9页

课时跟踪训练：第一章 有理数 一．选择题 ‎1．比﹣4小的数是（　　）‎ A．﹣2 B．﹣1 C．﹣6 D．6‎ ‎2．有理数a，b在数轴上的位置如图所示，则下列代数式值是负数的是（　　）‎ A．a+b B．﹣ab C．a﹣b D．﹣a+b ‎3．用四舍五入法按要求对0.64247分别取近似值，其中错误的是（　　）‎ A．精确到千分位得到0.643 ‎ B．精确到百分位得到0.64 ‎ C．精确到0.1得到0.6 ‎ D．精确到0.0001得到0.6425‎ ‎4．下列计算错误的是（　　）‎ A．（﹣5）+5＝0 B．[﹣]×（﹣2）3＝ ‎ C．（﹣1）3+（﹣1）2＝0 D．4÷2×＝2‎ ‎5．2019年10月1日，庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行，随后举行的阅兵仪式备受国内外关注．本次阅兵仪式是新中国成立70年以来规模最大、受检阅人数最多的一次，彰显了我国强大的国防实力．央视新闻置顶的微博#国庆阅兵#在10月1日下午6点阅读次数就超过34亿．其中34亿用科学记数法可表示为（　　）‎ A．0.34×109 B．3.4×108 C．3.4×109 D．34×109‎ ‎6．若|m|＝5，|n|＝7，m+n＜0，则m﹣n的值是（　　）‎ A．﹣12或﹣2 B．﹣2或12 C．12或2 D．2或﹣12‎ ‎7．如图，检测4个排球，其中质量超过标准的克数记为正数，不足的克数记为负数，从轻重的角度，下列最接近标准的是（　　）‎ A． B． C． D．‎ ‎8．已知x，y都是整数，若x，y的积等于8，且x﹣y是负数，则|x+y|的值有（　　）个．‎ A．1 B．2 C．3 D．4‎ ‎9．我们规定一种运算：a★b＝ab﹣a+b，其中a，b都是有理数，则a★b+a★（a﹣b）等于（　　）‎ A．a2﹣a B．a2+a C．a2﹣b D．b2﹣a ‎10．有理数a，b，c在数轴上对应的点的位置如图所示，则下列各式正确的个数有（　　）‎ ‎①abc＞0；②a﹣b+c＜0；③；④|a+b|﹣|b﹣c|+|a﹣c|＝﹣2c．‎ A．4个 B．3个 C．2个 D．1个 二．填空题 ‎11．太平洋最深处的马里纳海沟低于海平面11034m，它的海拔高度可表示为　 　．‎ ‎12．表示x，y两数的点在数轴上的位置如图所示，则|y+x|＝　 　．‎ ‎13．a为绝对值小于2019的所有整数的和，则2a的值为　 　．‎ ‎14．将12.4259精确到0.01得到的近似数是　 　．‎ ‎15．有两个蓄水池分别有水8立方米和12立方米，如果两个水池容量足够大，那么往其中一个水池注水　 　立方米，才能使其中一个水池的蓄水量是另一个水池蓄水量的．‎ ‎16．若a是绝对值最小的有理数，b是最大的负整数，c是倒数等于它本身的数，则代数式a﹣b+c的值为　 　．‎ 三．解答题 ‎17．计算：‎ ‎（1）（﹣5）﹣4÷（﹣2）+（﹣9）‎ ‎（2）﹣42+÷×（﹣2）2‎ ‎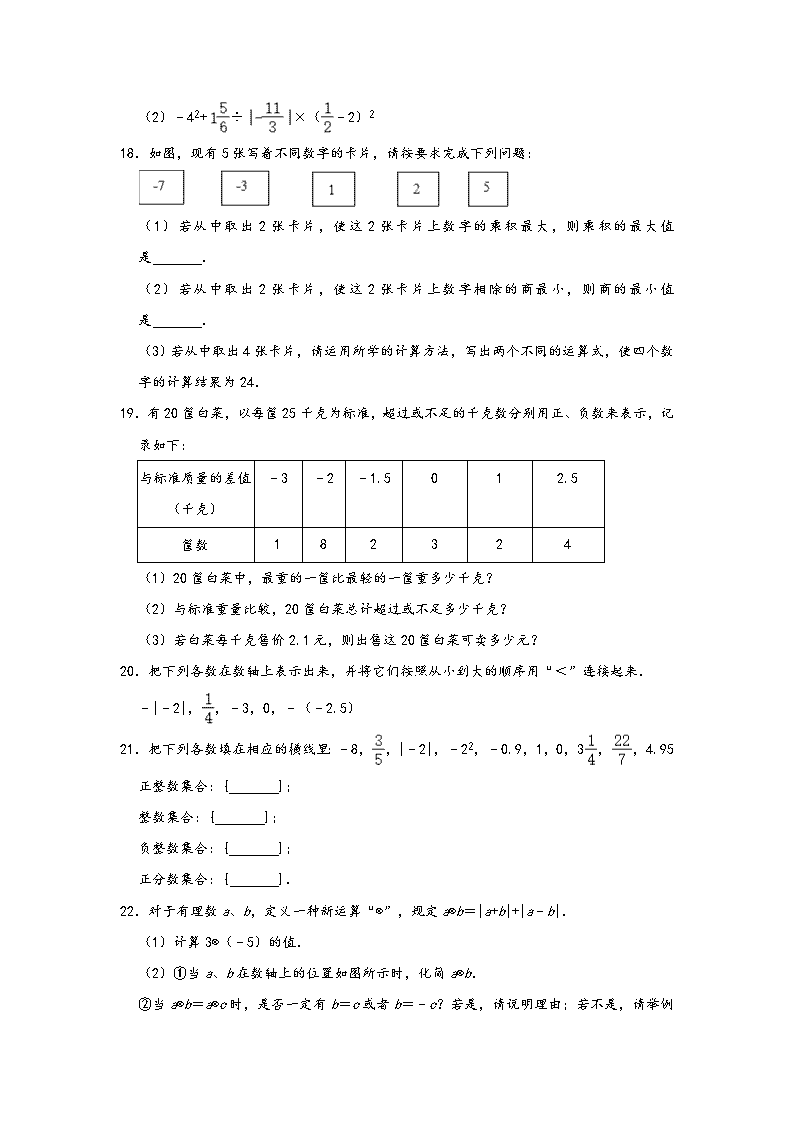18．如图，现有5张写着不同数字的卡片，请按要求完成下列问题：‎ ‎（1）若从中取出2张卡片，使这2张卡片上数字的乘积最大，则乘积的最大值是　 　．‎ ‎（2）若从中取出2张卡片，使这2张卡片上数字相除的商最小，则商的最小值是　 　．‎ ‎（3）若从中取出4张卡片，请运用所学的计算方法，写出两个不同的运算式，使四个数字的计算结果为24．‎ ‎19．有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：‎ 与标准质量的差值（千克）‎ ‎﹣3‎ ‎﹣2‎ ‎﹣1.5‎ ‎0‎ ‎1‎ ‎2.5‎ 筐数 ‎1‎ ‎8‎ ‎2‎ ‎3‎ ‎2‎ ‎4‎ ‎（1）20筐白菜中，最重的一筐比最轻的一筐重多少千克？‎ ‎（2）与标准重量比较，20筐白菜总计超过或不足多少千克？‎ ‎（3）若白菜每千克售价2.1元，则出售这20筐白菜可卖多少元？‎ ‎20．把下列各数在数轴上表示出来，并将它们按照从小到大的顺序用“＜”连接起来．‎ ‎﹣|﹣2|，，﹣3，0，﹣（﹣2.5）‎ ‎21．把下列各数填在相应的横线里：﹣8，，|﹣2|，﹣22，﹣0.9，1，0，3，，4.95‎ 正整数集合：{　 　}；‎ 整数集合：{　 　}；‎ 负整数集合：{　 　}；‎ 正分数集合：{　 　}．‎ ‎22．对于有理数a、b，定义一种新运算“⊗”，规定a⊗b＝|a+b|+|a﹣b|．‎ ‎（1）计算3⊗（﹣5）的值．‎ ‎（2）①当a、b在数轴上的位置如图所示时，化简a⊗b．‎ ‎②当a⊗b＝a⊗c时，是否一定有b＝c或者b＝﹣c ‎？若是，请说明理由；若不是，请举例说明．‎ ‎23．一次数学测验后，王老师把某一小组10名同学的成绩以平均成绩为基准，并以高于平均成绩记为“+”，分别记为+10分，﹣5分，0分，+8分，﹣3分，+6分，﹣5分，﹣3分，+4分，﹣12分，通过计算知道这10名同学的平均成绩是82分．‎ ‎（1）这一小组成绩最高分与最低分相差多少分？‎ ‎（2）如果成绩不低于80分为优秀，那么这10名同学在这次数学测验中优秀率是百分之几？‎ 参考答案 一．选择题 ‎1．解：∵﹣6＜﹣4＜﹣2＜﹣1＜6，‎ ‎∴比﹣4小的数是﹣6．‎ 故选：C．‎ ‎2．解：∵﹣1＜a＜0，b＞1，‎ ‎∴a+b＞0，﹣ab＞0，a﹣b＜0，﹣a+b＞0，‎ 故选：C．‎ ‎3．解：0.64247，精确到千分位得到0.642，精确到百分位得到0.64，精确到0.1得到0.6，精确到0.0001得到0.6425．‎ 故选：A．‎ ‎4．解：∵（﹣5）+5＝0，故选项A正确；‎ ‎∵（﹣）×（﹣2）3＝，故选项B正确；‎ ‎∵（﹣1）3+（﹣1）2＝（﹣1）+1＝0，故选项C正确；‎ ‎∵4÷2×＝4×＝1，故选项D错误；‎ 故选：D．‎ ‎5．解：34亿＝34 0000 0000＝3.4×109，‎ 故选：C．‎ ‎6．解：∵|m|＝5，|n|＝7，且m+n＜0，‎ ‎∴m＝5，n＝﹣7；m＝﹣5，n＝﹣7，‎ 可得m﹣n＝12或2，‎ 则m﹣n的值是12或2．‎ 故选：C．‎ ‎7．解：通过求4个排球的绝对值得：‎ ‎|+3.5|＝3.5，|﹣2.3|＝2.3，|+0.8|＝0.8，|﹣0.6|＝0.6，‎ ‎﹣0.6的绝对值最小．‎ 所以这个球是最接近标准的球．‎ 故选：D．‎ ‎8．解：∵x，y都是整数，x，y的积等于8，且x﹣y是负数，‎ ‎∴x＝﹣8，y＝﹣1或x＝﹣4，y＝﹣2或x＝1，y＝8或x＝2，y＝4，‎ ‎∴|x+y|＝9或6，一共2个．‎ 故选：B．‎ ‎9．解：根据题中的新定义得：原式＝ab﹣a+b+a（a﹣b）﹣a+a﹣b＝ab﹣a+b+a2﹣ab﹣a+a﹣b＝a2﹣a，‎ 故选：A．‎ ‎10．解：∵由数轴可得：b＜c＜0＜a，|b|＞|c|＞|a|‎ ‎∴abc＞0，①正确；‎ a﹣b+c＞0，②错误；‎ ‎++＝1﹣1﹣1＝﹣1，③正确；‎ ‎|a+b|﹣|b﹣c|+|a﹣c|＝﹣a﹣b﹣（c﹣b）+a﹣c ‎＝﹣a﹣b﹣c+b+a﹣c ‎＝﹣2c ‎④正确．‎ 综上，正确的个数为3个．‎ 故选：B．‎ 二．填空题（共6小题）‎ ‎11．解：太平洋最深处的马里纳海沟低于海平面11034m，它的海拔高度可表示为﹣11034m，‎ 故答案为﹣11034m．‎ ‎12．解：由x，y两数的点在数轴上的位置可得：x+y＜0，‎ ‎∴|x+y|＝﹣（x+y）＝﹣x﹣y，‎ 故答案为：﹣x﹣y．‎ ‎13．解：绝对值小于2019的所有整数有：﹣2018、﹣2017、…、﹣1、0、1、…、2017、2018，‎ 它们的和是：‎ a＝（﹣2018+2018）+（﹣2017+2017）+…+（﹣1+1）+0＝0，‎ ‎∴2a＝0．‎ 故答案为：0．‎ ‎14．解：12.4259≈12.43（精确到0.01）．‎ 故答案为：12.43．‎ ‎15．解：分两种情况进行解答，‎ ‎（1）向“原来有8立方米”的水池注水，设注水量为x立方米，‎ ‎①若“原来有8立方米的水池”的蓄水量是“原来有12立方米的水池”的蓄水量的，‎ 则有：8+x＝12×，‎ 解得，x＝1，‎ ‎②若“原来有12立方米的水池”的蓄水量是“原来有8立方米的水池”的蓄水量的，‎ 则有：（8+x）×＝12，‎ 解得，x＝8，‎ ‎（2）向“原来有12立方米”的水池注水，设注水量为x立方米，‎ ‎①若“原来有8立方米的水池”的蓄水量是“原来有12立方米的水池”的蓄水量的，‎ 则有：8＝（12+x）×，‎ 解得，x＝﹣（不合题意，舍去），‎ ‎②若“原来有12立方米的水池”的蓄水量是“原来有8立方米的水池”的蓄水量的，‎ 则有：8×＝12+x，‎ 解得，x＝﹣6（不合题意，舍去），‎ 故答案为：1或8．‎ ‎16．解：∵a是绝对值最小的有理数，b是最大的负整数，c是倒数等于它本身的数，‎ ‎∴a＝0，b＝﹣1，c＝±1，‎ ‎∴a﹣b+c＝0﹣（﹣1）+（﹣1）＝0或a﹣b+c＝0﹣（﹣1）+1＝2．‎ 故答案为：0或2．‎ 三．解答题（共7小题）‎ ‎17．解：（1）（﹣5）﹣4÷（﹣2）+（﹣9）‎ ‎＝﹣5+2﹣9‎ ‎＝﹣12；‎ ‎（2）﹣42+÷×（﹣2）2‎ ‎＝﹣16+÷×（﹣）2‎ ‎＝﹣16+÷×‎ ‎＝﹣16+×‎ ‎＝﹣16+1‎ ‎＝﹣14．‎ ‎18．解：（1）若从中取出2张卡片，使这2张卡片上数字的乘积最大，则乘积的最大值是：（﹣7）×（﹣3）＝21，‎ 故答案为：21；‎ ‎（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，则商的最小值是：（﹣7）÷1＝﹣7，‎ 故答案为：﹣7；‎ ‎（3）由题意可得，‎ 如果抽取的数字是﹣7，﹣3，1，2，‎ 则（﹣7）×（﹣3）+1+2＝24，（﹣7+1﹣2）×（﹣3）＝24；‎ 如果抽取的数字是﹣3，1，2，5，‎ 则（1﹣5）×（﹣3）×2＝24，[5﹣（﹣3）]×（1+2）＝24．‎ ‎19．解：（1）最重的一筐超过2.5千克，最轻的差3千克，求差即可2.5﹣（﹣3）＝5.5（千克），‎ 故最重的一筐比最轻的一筐重5.5千克；‎ ‎（2）1×（﹣3）+8×（﹣2）+2×（﹣1.5）+3×0+1×2+4×2.5‎ ‎＝﹣3﹣16﹣3+2+10‎ ‎＝﹣10（千克）．‎ 故20筐白菜总计不足10千克；‎ ‎（3）2.1×（25×20﹣10）‎ ‎＝2.1×490‎ ‎＝1029（元）．‎ 故出售这20筐白菜可卖1029元．‎ ‎20．解：，‎ ‎﹣3＜﹣|﹣2|＜0＜＜﹣（﹣2.5）．‎ ‎21．解：因为|﹣2|＝2，﹣22＝﹣4，‎ 所以正整数有：|﹣2|，1；‎ 整数有：﹣8，|﹣2|，﹣22，1，0；‎ 负整数有：﹣8，﹣22；‎ 正分数有：，3，，4.95‎ 故答案为：|﹣2|，1；﹣8，|﹣2|，﹣22，1，0；﹣8，﹣22；‎ ‎，3，，4.95．‎ ‎22．解：（1）根据题中的新定义得：3⊗（﹣5）＝|3+（﹣5）|+|3﹣（﹣5）|＝2+8＝10；‎ ‎（2）①从a，b在数轴上的位置可得a+b＜0，a﹣b＞0，‎ ‎∴a⊗b＝|a+b|+|a﹣b|＝﹣（a+b）+（a﹣b）＝﹣2b；‎ ‎②由a⊗b＝a⊗c得：|a+b|+|a﹣b|＝|a+c|+|a﹣c|，‎ 不一定有b＝c或者b＝﹣c，‎ 例如：取a＝5，b＝4，c＝3，则|a+b|+|a﹣b|＝|a+c|+|a﹣c|＝10，‎ 此时等式成立，但b≠c且b≠﹣c．‎ ‎23．解：（1）+10﹣（﹣12）＝22（分）．‎ 答：这一小组成绩最高分与最低分相差22分；‎ ‎（2）5÷10×100%＝50%．‎ 故这10名同学在这次数学测验中优秀率是50%．‎