2020七年级数学上册 第四章 几何图形初步单元综合测试卷（含解析）（新版）新人教版 18页

第四章 几何图形初步 考试时间：120分钟；满分：150分 学校:___________姓名：___________班级：___________考号：___________‎ 题号 一 二 三 总分 得分 ‎　‎ ‎ 评卷人 ‎ ‎ 得 分 ‎ ‎ ‎ ‎ ‎ 一．选择题（共10小题，满分40分，每小题4分）‎ ‎1．（4分）下列几何体中，是圆柱的为（　　）‎ ‎ ‎ A B C D ‎2．（4分）下列各组图形中都是平面图形的是（　　）‎ A．三角形、圆、球、圆锥 B．点、线段、棱锥、棱柱 C．角、三角形、正方形、圆 D．点、角、线段、长方体 ‎3．（4分）将下列各选项中的平面图形绕轴旋转一周，可得到如图所示的立体图形的是（　　）‎ ‎ ‎ A B C D ‎4．（4分）在同一条直线上依次有A，B，C，D四个点，若CD﹣BC=AB，则下列结论正确的是（　　）‎ A．B是线段AC的中点 B．B是线段AD的中点 C．C是线段BD的中点 D．C是线段AD的中点 ‎5．（4分）工人师傅在给小明家安装晾衣架时，一般先在阳台天花板上选取两个点，然后再进行安装．这样做的数学原理是（　　）‎ A．过一点有且只有一条直线 18‎ B．两点之间，线段最短 C．连接两点之间的线段叫两点间的距离 D．两点确定一条直线 ‎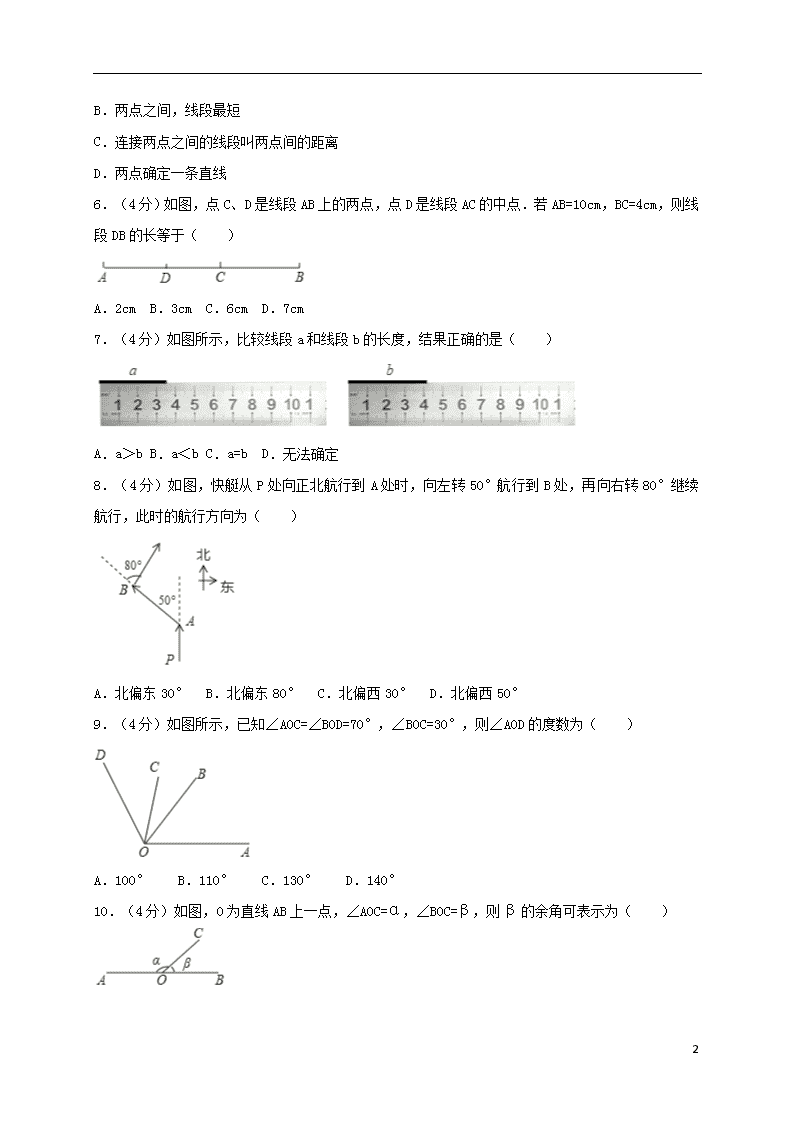6．（4分）如图，点C、D是线段AB上的两点，点D是线段AC的中点．若AB=10cm，BC=4cm，则线段DB的长等于（　　）‎ A．2cm B．3cm C．6cm D．7cm ‎7．（4分）如图所示，比较线段a和线段b的长度，结果正确的是（　　）‎ A．a＞b B．a＜b C．a=b D．无法确定 ‎8．（4分）如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时的航行方向为（　　）‎ A．北偏东30° B．北偏东80° C．北偏西30° D．北偏西50°‎ ‎9．（4分）如图所示，已知∠AOC=∠BOD=70°，∠BOC=30°，则∠AOD的度数为（　　）‎ A．100° B．110° C．130° D．140°‎ ‎10．（4分）如图，O为直线AB上一点，∠AOC=α，∠BOC=β，则β的余角可表示为（　　）‎ 18‎ A．（α+β） B．α C．（α﹣β） D．β ‎　‎ ‎ 评卷人 ‎ ‎ 得 分 ‎ ‎ ‎ ‎ ‎ 二．填空题（共4小题，满分20分，每小题5分）‎ ‎11．（5分）如图是正方体的一个表面展开图，在这个正方体中，与“晋”字所在面相对的面上的汉字是　 　．‎ ‎12．（5分）直线AB，BC，CA的位置关系如图所示，则下列语句：①点A在直线BC上；②直线AB经过点C；③直线AB，BC，CA两两相交；④点B是直线AB，BC，CA的公共点，正确的有　 　（只填写序号）．‎ ‎13．（5分）青青同学把一张长方形纸折了两次，如图，使点A，B都落在DG上，折痕分别是DE，DF，则∠EDF的度数为　 　．‎ ‎14．（5分）将一副三角板如图放置，若∠AOD=20°，则∠BOC的大小为　 　．‎ ‎　‎ 18‎ ‎ 评卷人 ‎ ‎ 得 分 ‎ ‎ ‎ ‎ ‎ 三．解答题（共9小题，满分90分）‎ ‎15．（8分）如图是一个正方体的平面展开图，标注了A字母的是正方体的正面，如果正方体的左面与右面标注的式子相等．‎ ‎（1）求x的值；‎ ‎（2）求正方体的上面和右面的数字和．‎ ‎16．（8分）如图，已知线段AB=6，延长线段AB到C，使BC=2AB，点D是AC的中点．求：‎ ‎（1）AC的长；‎ ‎（2）BD的长．‎ ‎17．（8分）如图，已知A、B、C、D四点，根据下列语句画图 ‎（1）画直线AB ‎（2）连接AC、BD，相交于点O ‎（3）画射线AD、BC，交于点P．‎ ‎18．（8分）如图，已知线段AB，按下列要求完成画图和计算：‎ ‎（1）延长线段AB到点C，使BC=2AB，取AC中点D；‎ ‎（2）在（1）的条件下，如果AB=4，求线段BD的长度．‎ ‎19．（10分）如图，已知在△ABC中，AB=AC．‎ 18‎ ‎（1）试用直尺和圆规在AC上找一点D，使AD=BD（不写作法，但需保留作图痕迹）．‎ ‎（2）在（1）中，连接BD，若BD=BC，求∠A的度数．‎ ‎20．（10分）如图，△ABC中，BC＞AC，∠C=50°．‎ ‎（Ⅰ）作图：在CB上截取CD=CA，连接AD，过点D作DE⊥AC，垂足为E；（要求：尺规作图，保留作图痕迹，不写作法）‎ ‎（Ⅱ）求∠ADE的度数．‎ ‎21．（12分）如图，O是直线AB上的一点，∠COD是直角，OE平分∠BOC．‎ ‎（1）若∠AOC=30°，求∠DOE的度数；‎ ‎（2）若∠AOC=α，直接写出∠DOE的度数（用含α的代数式表示）；‎ ‎（3）在（1）的条件下，∠BOC的内部有一射线OG，射线OG将∠BOC分为1：4两部分，求∠DOG的度数．‎ ‎22．（12分）如图，将书页一角斜折过去，使角的顶点A落在A′处，BC为折痕，BD平分∠A′BE，求∠CBD的度数．‎ ‎23．（14分）如图1，已知∠MON=140°，∠AOC与∠BOC互余，OC平分∠MOB，‎ 18‎ ‎（1）在图1中，若∠AOC=40°，则∠BOC=　 　°，∠NOB=　 　°．‎ ‎（2）在图1中，设∠AOC=α，∠NOB=β，请探究α与β之间的数量关系（ 必须写出推理的主要过程，但每一步后面不必写出理由）；‎ ‎（3）在已知条件不变的前提下，当∠AOB绕着点O顺时针转动到如图2的位置，此时α与β之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出此时α与β之间的数量关系．‎ ‎　‎ 18‎ ‎2018年秋七年级上学期 第四章 几何图形初步 单元测试卷 参考答案与试题解析 ‎　‎ 一．选择题（共10小题，满分40分，每小题4分）‎ ‎1．‎ ‎【分析】根据立体图形的定义及其命名规则逐一判断即可．‎ ‎【解答】解：A、此几何体是圆柱体；‎ B、此几何体是圆锥体；‎ C、此几何体是正方体；‎ D、此几何体是四棱锥；‎ 故选：A．‎ ‎【点评】本题主要考查立体图形，解题的关键是认识常见的立体图形，如：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等．能区分立体图形与平面图形，立体图形占有一定空间，各部分不都在同一平面内．‎ ‎　‎ ‎2．‎ ‎【分析】根据平面图形定义：一个图形的各部分都在同一个平面内的图形是平面图形可得答案．‎ ‎【解答】解：A、球、圆锥是立体图形，错误；‎ B、棱锥、棱柱是立体图形，错误；‎ C、角、三角形、正方形、圆是平面图形，正确；‎ D、长方体是立体图形，错误；‎ 故选：C．‎ ‎【点评】此题主要考查了平面图形，关键是掌握平面图形的定义．‎ ‎　‎ ‎3．‎ ‎【分析】面动成体．由题目中的图示可知：此圆台是直角梯形转成圆台的条件是：绕垂直于底的腰旋转．‎ ‎【解答】解：A、上面小下面大，侧面是曲面，故A正确；‎ B、上面大下面小，侧面是曲面，故B错误；‎ C、是一个圆台，故C错误；‎ 18‎ D、下、上面一样大、侧面是曲面，故D错误；‎ 故选：A．‎ ‎【点评】本题考查直角梯形转成圆台的条件：应绕垂直于底的腰旋转．‎ ‎　‎ ‎4．‎ ‎【分析】直接利用已知画出图形，进而分析得出答案．‎ ‎【解答】解：如图所示：‎ ‎，‎ 符合CD﹣BC=AB，则C是线段AD的中点．‎ 故选：D．‎ ‎【点评】此题主要考查了直线、线段，正确画出符合题意的图形是解题关键．‎ ‎　‎ ‎5．‎ ‎【分析】直接利用直线的性质分析得出答案．‎ ‎【解答】解：工人师傅在给小明家安装晾衣架时，一般先在阳台天花板上选取两个点，然后再进行安装．‎ 这样做的数学原理是：两点确定一条直线．‎ 故选：D．‎ ‎【点评】此题主要考查了直线的性质，正确把握直线的性质是解题关键．‎ ‎　‎ ‎6．‎ ‎【分析】先根据线段的和差关系求出AC，再根据中点的定义求得CD的长，再根据BD=CD+BC即可解答．‎ ‎【解答】解：∵AB=10，BC=4，‎ ‎∴AC=AB﹣BC=6，‎ ‎∵点D是AC的中点，‎ ‎∴AD=CD=AC=3．‎ ‎∴BD=BC+CD=4+3=7cm，‎ 故选：D．‎ 18‎ ‎【点评】此题考查了两点间的距离，根据是熟练掌握线段的和差计算，以及中点的定义．‎ ‎　‎ ‎7．‎ ‎【分析】根据刻度尺对两条线段进行测量的结果解答即可．‎ ‎【解答】解：a=3.5，b=4.2，‎ 可得：a＜b，‎ 故选：B．‎ ‎【点评】此题考查线段的比较，要想得到准确的结果，必须进行测量．‎ ‎　‎ ‎8．‎ ‎【分析】根据平行线的性质，可得∠2，根据角的和差，可得答案．‎ ‎【解答】解：如图 ‎，‎ AP∥BC，‎ ‎∴∠2=∠1=50°．‎ ‎∠3=∠4﹣∠2=80°﹣50°=30°，‎ 此时的航行方向为北偏东30°，‎ 故选：A．‎ ‎【点评】本题考查了方向角，利用平行线的性质得出∠2是解题关键．‎ ‎　‎ ‎9．‎ ‎【分析】根据图形和题目中的条件，可以求得∠AOB的度数和∠COD的度数，从而可以求得∠AOD的度数．‎ ‎【解答】解：∵∠AOC=70°，∠BOC=30°，‎ ‎∴∠AOB=40°；‎ 18‎ 同理可得，∠COD=40°．‎ ‎∴∠AOD=∠AOB+∠BOC+∠COD=40°+30°+40°=110°，‎ 故选：B．‎ ‎【点评】本题考查角的计算，解答本题的关键是明确角之间的关系，利用数形结合的思想解答．‎ ‎　‎ ‎10．‎ ‎【分析】根据补角的性质，余角的性质，可得答案．‎ ‎【解答】解：由邻补角的定义，得 ‎∠α+∠β=180°，‎ 两边都除以2，得 ‎（α+β）=90°，‎ β的余角是（α+β）﹣β=（α﹣β），‎ 故选：C．‎ ‎【点评】本题考查了余角和补角，利用余角、补角的定义是解题关键．‎ ‎　‎ 二．填空题（共4小题，满分20分，每小题5分）‎ ‎11．‎ ‎【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．‎ ‎【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，‎ ‎“晋”与“祠”是相对面，‎ ‎“汾”与“酒”是相对面，‎ ‎“恒”与“山”是相对面．‎ 故答案为：祠．‎ ‎【点评】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．‎ ‎　‎ ‎12．‎ ‎【分析】根据直线与点的位置关系即可求解．‎ ‎【解答】解：①点A在直线BC上是错误的；‎ 18‎ ‎②直线AB经过点C是错误的；‎ ‎③直线AB，BC，CA两两相交是正确的；‎ ‎④点B是直线AB，BC，CA的公共点是错误的．‎ 故答案为：③．‎ ‎【点评】考查了直线、射线、线段，关键是熟练掌握直线、射线、线段的定义，是基础题型．‎ ‎　‎ ‎13．‎ ‎【分析】先利用折叠的性质得到∠BDF=∠GDF，∠ADE=∠GDA，所以∠FDG+∠GDE=∠BDA，然后利用平角的定义可计算出∠DEF的度数．‎ ‎【解答】解：∵长方形纸折了两次，如图，使点A，B都落在DG上，折痕分别是DE，DF，‎ ‎∴∠BDF=∠GDF，∠ADE=∠GDA，‎ ‎∴∠FDG+∠GDE=∠BDA=×180°=90°，‎ 即∠DEF=90°．‎ 故答案为90°．‎ ‎【点评】本题考查了角度的计算：利用角平分线的定义得到相等的两个角．也考查了折叠的性质．‎ ‎　‎ ‎14．‎ ‎【分析】先求出∠COA和∠BOD的度数，代入∠BOC=∠COA+∠AOD+∠BOD求出即可．‎ ‎【解答】解：∵∠AOD=20°，∠COD=∠AOB=90°，‎ ‎∴∠COA=∠BOD=90°﹣20°=70°，‎ ‎∴∠BOC=∠COA+∠AOD+∠BOD=70°+20°+70°=160°，‎ 故答案为：160°．‎ ‎【点评】本题考查了度、分、秒之间的换算，余角的应用，解此题的关键是求出∠COA和∠BOD的度数，注意：已知∠A，则∠A的余角=90°﹣∠A．‎ ‎　‎ 三．解答题（共9小题，满分90分）‎ ‎15．‎ ‎【分析】（1）正方体的表面展开图，相对的面之间一定相隔一个正方形确定出相对面，然后列出方程求解即可；‎ 18‎ ‎（2）确定出上面和右面上的两个数字3x﹣2和1，然后相加即可．‎ ‎【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，‎ ‎“A”与“﹣2”是相对面，‎ ‎“3”与“1”是相对面，‎ ‎“x”与“3x﹣2”是相对面，‎ ‎（1）∵正方体的左面与右面标注的式子相等，‎ ‎∴x=3x﹣2，‎ 解得x=1；‎ ‎（2）∵标注了A字母的是正方体的正面，左面与右面标注的式子相等，‎ ‎∴上面和右面上的两个数字3x﹣2和1，‎ ‎∴1+3x﹣2=2‎ ‎【点评】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．‎ ‎　‎ ‎16．‎ ‎【分析】（1）根据BC=2AB求出BC，结合图形计算即可；‎ ‎（2）根据线段中点的定义求出AD，计算即可．‎ ‎【解答】解：（1）∵BC=2AB，‎ ‎∴BC=2×6=12，‎ ‎∴AC=AB+BC=18；‎ ‎（2）∵点D是AC的中点，‎ ‎∴AD=AC=9，‎ ‎∴BD=AD﹣AB=3．‎ ‎【点评】本题考查的是两点间的距离的计算，掌握线段中点的定义、线段的计算是解题的关键．‎ ‎　‎ ‎17．‎ ‎【分析】（1）过A，B画直线即可；‎ ‎（2）连接AC、BD，即可得到点O；‎ ‎（3）画射线AD、BC，即可得到点P．‎ 18‎ ‎【解答】解：（1）如图所示，直线AB即为所求；‎ ‎（2）如图所示，线段AC，BD即为所求；‎ ‎（3）如图所示，射线AD、BC即为所求．‎ ‎【点评】本题主要考查了直线，射线和线段的简单作图，解答此题需要熟练掌握直线、射线、线段的性质．‎ ‎　‎ ‎18．‎ ‎【分析】（1）根据线段的关系，可得BC，‎ ‎（2）根据线段的和差，可得AC的长，根据线段中点的性质，可得AD，根据线段的和差，可得答案．‎ ‎【解答】解：（1）如图：‎ ‎（2）∵BC=2AB，且AB=4，‎ ‎∴BC=8．‎ ‎∴AC=AB+BC=8+4=12．‎ ‎∵D为AC中点，（已知）‎ ‎∴AD=AC=6．（线段中点的定义）‎ ‎∴BD=AD﹣AB=6﹣4=2．‎ ‎【点评】本题考查了两点间的距离，利用线段的和差是解题关键．‎ ‎　‎ ‎19．‎ ‎【分析】（1）直接利用线段垂直平分线的性质得出符合题意的图形；‎ ‎（2）直接利用等腰三角形的性质结合三角形内角和定理得出答案．‎ 18‎ ‎【解答】解：（1）如图所示：‎ ‎（2）设∠A=x，‎ ‎∵AD=BD，‎ ‎∴∠DBA=∠A=x，‎ 在△ABD中 ‎∠BDC=∠A+∠DBA=2x，‎ 又∵BD=BC，‎ ‎∴∠C=∠BDC=2x，‎ 又∵AB=AC，‎ ‎∴∠ABC=∠C=2x，‎ 在△ABC中 ‎∠A+∠ABC+∠C=180°，‎ ‎∴x+2x+2x=180°，‎ ‎∴x=36°．‎ ‎【点评】此题主要考查了基本作图、等腰三角形的性质以及三角形内角和定理，正确掌握线段垂直平分线的性质是解题关键．‎ ‎　‎ ‎20．‎ ‎【分析】（Ⅰ）以C为圆心CA为半径画弧交CB于D，作DE⊥AC即可；‎ ‎（Ⅱ）根据三角形内角和定理计算即可；‎ ‎【解答】解：（Ⅰ）如图，点D就是所求作的点，线段AD，DE就是所要作的线段．‎ 18‎ ‎（Ⅱ）∵CA=CD，‎ ‎∴，‎ 在Rt△ADE中，‎ ‎∠ADE=90°﹣∠DAE=90°﹣65°=25°．‎ ‎【点评】本题考查作图﹣复杂作图，三角形的内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．‎ ‎　‎ ‎21．‎ ‎【分析】（1）求出∠BOD，求出∠BOC，根据角平分线求出∠BOE，代入∠DOE=∠BOE﹣∠BOD求出即可．‎ ‎（2）由第（1）问的求法，可以直接写出∠DOE的度数；‎ ‎（3）∠BOC的内部有一射线OG，射线OG将∠BOC分为1：4两部分，题目没有明确射线OG位于DC中间或DB中间，所以在两种情况下分别求出∠DOG的度数即可．‎ ‎【解答】解：（1）∵∠COD是直角，∠AOC=30°，‎ ‎∴∠BOD=180°﹣90°﹣30°=60°，‎ ‎∴∠COB=90°+60°=150°，‎ ‎∵OE平分∠BOC，‎ ‎∴∠BOE=∠BOC=75°，‎ ‎∴∠DOE=∠BOE﹣∠BOD=75°﹣60°=15°．‎ ‎（2）∵∠COD是直角，∠AOC=α，‎ ‎∴∠BOD=180°﹣90°﹣α=90°﹣α，‎ ‎∴∠COB=90°+90°﹣α=180°﹣α，‎ ‎∵OE平分∠BOC，‎ ‎∴∠BOE=∠BOC=90°﹣α，‎ ‎∴∠DOE=∠BOE﹣∠BOD=90°﹣α﹣（90°﹣α）=α．‎ 18‎ ‎（3）①当射线OG位于DC之间时，如图1所示 ‎∵∠AOC=30°，射线OG将∠BOC分为1：4两部分，‎ ‎∴∠BOC=150°，∠COG=30°，∠BOG=120°‎ 由（1）知：∠BOD=60°，‎ ‎∴∠DOG=∠BOG﹣∠BOD=120°﹣60°=60°‎ ‎②当射线OG位于DB之间时，如图2所示 ‎∵∠AOC=30°，射线OG将∠BOC分为1：4两部分，‎ ‎∴∠BOC=150°，∠COG=120°，∠BOG=30°‎ 由（1）知：∠BOD=60°，‎ ‎∴∠DOG=∠BOD﹣∠BOG=60°﹣30°=30°‎ ‎【点评】本题考查了角平分线的定义，是基础题，难度不大，掌握各角之间的关系是解题的关键．‎ ‎　‎ ‎22．‎ ‎【分析】根据翻折变换的性质可得∠ABC=∠A′BC，再根据角平分线的定义可得∠A′BD=∠EBD，再根据平角等于180°列式计算即可得解．‎ ‎【解答】解：由翻折的性质得，∠ABC=∠A′BC，‎ ‎∵BD平分∠A′BE，‎ ‎∴∠A′BD=∠EBD，‎ ‎∵∠ABC+∠A′BC+∠A′BD+∠EBD=180°，‎ ‎∴∠A′BC+∠A′BD=90°，‎ 即∠CBD=90°．‎ ‎【点评】本题考查了角的计算，主要利用了翻折变换的性质，角平分线的定义，熟记概念与性质是解题的关键．‎ ‎　‎ ‎23．‎ 18‎ ‎【分析】（1）先根据余角的定义计算∠BOC=50°，再由角平分线的定义计算∠BOM=100°，根据角的差可得∠BON的度数；‎ ‎（2）同理先计算∠MOB=2∠BOC=2（90°﹣α）=180°﹣2α，再根据∠BON=∠MON﹣∠BOM列等式即可；‎ ‎（3）同理可得∠MOB=180°﹣2α，再根据∠BON+∠MON=∠BOM列等式即可．‎ ‎【解答】（10分）‎ 解：（1）如图1，∵∠AOC与∠BOC互余，‎ ‎∴∠AOC+∠BOC=90°，‎ ‎∵∠AOC=40°，‎ ‎∴∠BOC=50°，‎ ‎∵OC平分∠MOB，‎ ‎∴∠MOC=∠BOC=50°，‎ ‎∴∠BOM=100°，‎ ‎∵∠MON=40°，‎ ‎∴∠BON=∠MON﹣∠BOM=140°﹣100°=40°，‎ 故答案为：50，40；…（4分）‎ ‎（2）解：β=2α﹣40°，理由是：‎ 如图1，∵∠AOC=α，‎ ‎∴∠BOC=90°﹣α，‎ ‎∵OC平分∠MOB，‎ ‎∴∠MOB=2∠BOC=2（90°﹣α）=180°﹣2α，…（5分）‎ 又∵∠MON=∠BOM+∠BON，‎ ‎∴140°=180°﹣2α+β，即β=2α﹣40°；（7分）‎ ‎（3）不成立，此时此时α与β之间的数量关系为：2α+β=40°，（8分）‎ 理由是：如图2，∵∠AOC=α，∠NOB=β，‎ ‎∴∠BOC=90°﹣α，‎ ‎∵OC平分∠MOB，‎ ‎∴∠MOB=2∠BOC=2（90°﹣α）=180°﹣2α，‎ ‎∵∠BOM=∠MON+∠BON，‎ ‎∴180°﹣2α=140°+β，即2α+β=40°，‎ 18‎ 答：不成立，此时此时α与β之间的数量关系为：2α+β=40°，（10分）‎ ‎【点评】本题考查了角平分线定义，角的有关计算的应用，解此题的关键是求出注意利用数形结合的思想，熟练掌握角的和与差的关系．‎ ‎　‎ 18‎